6.6 Persamaan Lokus yang Melibatkan Jarak di antara Dua Titik
1. Persamaan lokus bagi suatu titik bergerak P (x, y) supaya jaraknya (r) dari suatu titik tetap (x1, y1) adalah malar.
(x– x1)2 + (y – y1)2= r2
(x– x1)2 + (y – y1)2= r2
2. Persamaan lokus bagi suatu titik bergerak P (x, y) supaya jaraknya sentiasa malar dari dua titik tetap (x1, y1) dan (x1, y1) dengan nisbah m : n ialah
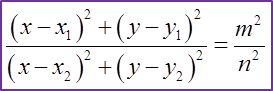
3. Persamaan lokus bagi suatu titik bergerak P (x, y) supaya jaraknya sentiasa malar dari dua titik tetap A dan B adalah pembahagi dua sama serenjang garis AB.
Contoh 1:
Cari persamaan lokus bagi titik bergerak P (x, y) supaya jaraknya sentiasa 5 unit dari suatu titik tetap Q (2, 4).
Penyelesaian:
(x – x1)2+ (y – y1)2 = r2
(x – 2)2 + (y – 4)2 = 52
x2 – 4x + 4 + y2 – 8y + 16 = 25
x2 + y2– 4x – 8y – 5 = 0
Contoh 2:
Cari persamaan lokus bagi titik bergerak P (x, y) supaya jaraknya dari titik A(–2, 3) dan titik B (4, –1) adalah sama.
Penyelesaian:
PA = PB
Kuasa duakan kedua-dua belah persamaan
(x + 2)2 + (y – 3)2 = (x – 4)2+ (y + 1)2
x2 + 2x + 4 + y2 – 6y + 9 = x2 – 8x + 16 + y2 + 2y + 1
10x – 8y – 4 = 0
Jadi, persamaan lokus titik P ialah, 10x – 8y – 4 = 0
Contoh 3:
A (2, 0) dan B (0, -2) adalah dua titik tetap. Titik P bergerak dengan nisbah supaya AP : PB = 1 : 2. Cari persamaan lokus bagi titik bergerak P.
Penyelesaian:
AP: PB = 1: 2
Kuasa duakan kedua-dua belah persamaan
4[(x – 2)2 + y2] = x2 + (y + 2)2
4 (x2 – 4x + 4 + y2) = x2 + y2+ 4y + 4
4x2 – 16x + 16 + 4y2 = x2 + y2 + 4y + 4
3x2 + 3y2 – 16x – 4y + 12 = 0
Jadi, persamaan lokus titik P ialah, 3x2 + 3y2 – 16x – 4y +12 = 0