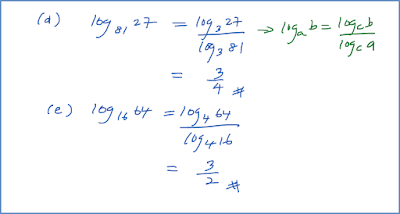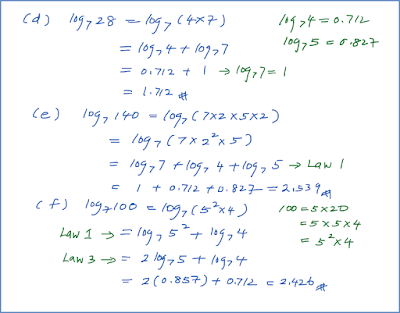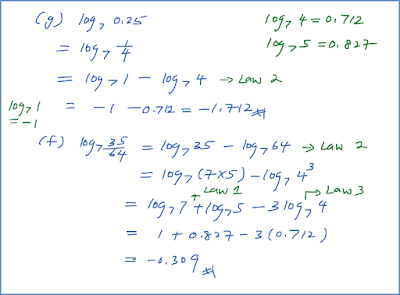Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2b Penukaran Asas Logaritma (Contoh Soalan)

Contoh 3:

Diberi bahawa log_p3 = h dan log_p 5 = k , ungkapkan setiap yang berikut dalam sebutan h dan k.

\begin{array}{l} (a) \log_{p} \frac{5}{3} \\ (b) \log_{15} 75 \end{array}

Penyelesaian:

Contoh 4:

Diberi bahawa log₃ x = b , ungkapkan log_x 9x dalam sebutan b.

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2b Penukaran Asas Logaritma

\begin{array}{l} \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \\ dan \\ \log_{a} b = \frac{1}{\log_{b} a} \end{array}

Contoh 1:

Cari nilai-nilai yang berikut:

(a) log₂₅ 100

(b) log₃ 0.45

Penyelesaian:

\begin{array}{l} (a) \log_{25} 100 \\ = \frac{\log_{10} 100}{\log_{10} 25} = \frac{10}{1.3979} = 7.154 \\ (b) \log_{3} 0.45 \\ = \frac{\log_{10} 0.45}{\log_{10} 3} = \frac{- 0.3468}{0.4771} = - 0.727 \end{array}

Contoh 2:

Cari nilai-nilai yang berikut:
(a) log₄ 8
(b) log₁₂₅ 5
(c) log₈₁ 27
(d) log₁₆ 64

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

Contoh 2:

Cari nilai bagi setiap yang berikut.

\begin{array}{l} (a) \log_{2} 7 + \log_{2} 12 + \log_{2} 21 \\ (b) 3 \log_{10} 5 + 2 \log_{10} 2 - \log_{10} 5 \\ (c) 2 \log_{10} 3 - \log_{10} 3 + \log_{10} 3 \frac{1}{3} \\ (d) \log_{3} 3 p + \log_{3} 3 q - \log_{3} p q \end{array}

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 13, 2016 by user

5.2a Hukum-hukum Logaritma (Contoh 3)

Contoh 3:

Diberi bahawa log₇4 = 0.712 dan log₇5 = 0.827, cari nilai bagi setiap yang berikut.

\begin{array}{l} (a) \log_{7} 20 \\ (b) \log_{7} 1 \frac{1}{4} \\ (c) \log_{7} 0.8 \\ (d) \log_{7} 28 \\ (e) \log_{7} 140 \\ (f) \log_{7} 100 \\ (g) \log_{7} 0.25 \\ (h) \log_{7} \frac{35}{64} \end{array}

Penyelesaian:

Bab 16 Ubahan

Posted on May 13, 2016 by user

5.1 Ubahan Langsung (Bahagian 1)

(A) Menentukan sama ada suatu kuantiti berubah secara langsung terhadap kuantiti yang lain

1. Jika suatu kuantiti y berubah secara langsung dengan suatu kuantiti x,

(a) y bertambah apabila x bertambah

(b) y berkurung apabila x berkurung

2. Suatu kuantiti y berubah secara langsung dengan suatu kuantiti x jika dan hanya jika

\frac{y}{x} = k

di mana k ialah pemalar.

3. yberubah secara langsung dengan x ditulis aebagai y α x.

4. Apabila y α x, maka graf y melawan x adalah satu garis lurusyang melalui asalan.

(B) Ungkapkan suatu ubahan langsung dalam bentuk persamaan yang melibatkan dua pemboleh ubah

Contoh 1:

Diberi bahawa yberubah secara langsung dengan x dan y = 20 apabila x = 36. Tulis ubahan langsung itu dalam bentuk persamaan.

Penyelesaian:

\begin{array}{l} y \propto x \\ y = k x \\ 20 = k (36) \\ k = \frac{20}{36} = \frac{4}{9} \to (C a r i k terdahulu) \\ ∴ y = \frac{4}{9} x \end{array}

(C) Mencari nilai bagi suatu pemboleh ubah dalam ubahan langsung

Jika y berubah secara langsung dengan x dan maklumat yang mencukupi diberi, maka nilai y atau x dapat dicari dengan menggunakan

\begin{array}{l} (a) y = k x, or \\ (b) \frac{y_{1}}{x_{1}} = \frac{y_{2}}{x_{2}} \end{array}

Contoh 2:

Diberi bahawa yberubah secara langsung dengan x dan y = 24 apabila x = 8, cari

(a) Persamaan yang mengaitkan y kapada x

(b) nilai bagi y apabila x = 6

Penyelesaian:

Kaedah 1: Guna y = kx

(a)

yα x

y= kx

Apabila y= 24, x = 8

24 = k (8)

k = 3

(b)

Apabila x= 6,

y = 3(6)

y = 18

\begin{array}{l} Kaedah 2 : Guna \frac{y_{1}}{x_{1}} = \frac{y_{2}}{x_{2}} \\ (a) \\ L e t x_{1} = 8 dan y_{1} = 24 \\ \frac{y_{1}}{x_{1}} = \frac{y_{2}}{x_{2}} \to \frac{24}{8} = \frac{y_{2}}{x_{2}} \\ \frac{3}{1} = \frac{y_{2}}{x_{2}} \to y_{2} = 3 x_{2} \\ ∴ y = 3 x \end{array}

\begin{array}{l} (b) \\ x_{1} = 8 dan y_{1} = 24 dan x_{2} = 6; cari y_{2} . \\ \frac{y_{1}}{x_{1}} = \frac{y_{2}}{x_{2}} \to \frac{24}{8} = \frac{y_{2}}{6} \\ y_{2} = \frac{24}{8} (6) \\ y_{2} = 18 \end{array}

\begin{array}{l} (c) \\ x_{1} = 8 dan y_{1} = 24 {dan y}_{2} = 36; cari x_{2} . \\ \frac{y_{1}}{x_{1}} = \frac{y_{2}}{x_{2}} \to \frac{24}{8} = \frac{36}{x_{2}} \\ 24 x_{2} = 36 \times 8 \\ x_{2} = 12 \end{array}

Bab 16 Ubahan

Posted on May 12, 2016 by user

5.2 Ubahan Songsang

Jika suatu kuantiti y berubah secara songsang dengan suatu kuantiti yang lain x, maka

(a) y bertambah apabila x berkurang,

(b) y berkurang apabila x bertambah.

(A) Menulis suatu ubahan songsang dalam bentuk persamaan

Suatu ubahan songsang dapat ditulis dalam bentuk persamaan,

y = \frac{k}{x}

di mana k ialah pemalar yang dapat ditentukan.

Contoh 1:

Diberi y berubah secara songsang dengan x dan y = 4 apabila x =10. Tulis satu persamaan yang mengaitkan x dan y.

Penyelesaian:

\begin{array}{l} y \propto \frac{1}{x} \to y = \frac{k}{x} \\ 4 = \frac{k}{10} \to k = 40 \\ ∴ y = \frac{40}{x} \end{array}

Contoh 2:

Diberi bahawa y = 3 apabila x = 6, cari persamaan yang mengaitkan x dan y jika:

(a) y \propto \frac{1}{x^{2}} (b) y \propto \frac{1}{x^{3}} (c) y \propto \frac{1}{\sqrt{x}}

Penyelesaian:

\begin{array}{l} (a) \\ y \propto \frac{1}{x^{2}} \to y = \frac{k}{x^{2}} \\ 3 = \frac{k}{6^{2}} \\ k = 3 \times 36 = 108 \\ ∴ y = \frac{108}{x^{2}} \end{array}

\begin{array}{l} (b) \\ y \propto \frac{1}{x^{3}} \to y = \frac{k}{x^{3}} \\ 3 = \frac{k}{6^{3}} \\ k = 3 \times 216 = 648 \\ ∴ y = \frac{648}{x^{3}} \end{array}

\begin{array}{l} (c) \\ y \propto \frac{1}{\sqrt{x}} \to y = \frac{k}{\sqrt{x}} \\ 3 = \frac{k}{\sqrt{6}} \\ k = 3 \times \sqrt{6} = 3 \sqrt{6} \\ ∴ y = \frac{3 \sqrt{6}}{\sqrt{x}} \end{array}

Bab 16 Ubahan

Posted on May 12, 2016 by user

5.1 Ubahan Langsung (Bahagian 2)

(D) Menyelesaikan masalah yang melibatkan ubahan langsung

1. Jika y α xⁿ, di mana n = ½ , 2, 3, maka persamaannya ialah y = kxⁿ di mana k ialah pemalar.

2. Graf y melawan xⁿ adalah satu garis lurus yang melalui asalan.

3. Jika y α xⁿ, dan diberi dengan maklumat yang mencukupi, maka nilai xatau niali y dapat ditentukan.

Contoh:

y berubah secara langsung dengan x³dan y = 54 apabila x = 3, cari

(a) nilai bagi x apabila y = 16

(b) nilai bagi y apabila x = 4

Penyelesaian:

Diberi y α x³, y = kx³

Apabila y = 54, x = 3,

54 = k (3)³

54 = 27k

k = 2

maka y = 2x³

(a) Apabila y = 16

16 = 2x³

x³= 8

x= 2

(b) Apabila x = 4

y = 2(4)³ = 128

Bab 16 Ubahan

Posted on May 12, 2016 by user

5.1 Ubahan Langsung (Contoh Soalan)

Contoh 1:

Diberi bahawa p berubah secara langsung dengan punca kuasa dua q dan p=12 apabila q=36,cari

(a) nilai bagi p apabila q=16

(b) nilai bagi q apabila p=18

Penyelesaian:

\begin{array}{l} p \propto \sqrt{q}, p = k \sqrt{q} \\ 12 = k \sqrt{36} \\ 12 = k (6) \\ k = 2 \\ p = 2 \sqrt{q} \end{array}

\begin{array}{l} (a) \\ p = 2 \sqrt{q} \\ p = 2 \sqrt{16} = 2 (4) \\ p = 8 \end{array}

\begin{array}{l} (b) \\ p = 2 \sqrt{q} \\ 18 = 2 \sqrt{q} \to 9 = \sqrt{q} \\ 9^{2} = q \\ q = 81 \end{array}

Bab 16 Ubahan

Posted on May 12, 2016 by user

5.3 Ubahan Tercantum

(A) Mewakili suatu ubahan tercantum dengan menggunakan simbol ‘α’

1. Jika satu pemboleh ubah berubah secara langsung dan/atau secara songsang dengan pemboleh ubah yang lain, hubungan ini dikenali sebagai ubahan tercantum.

2. ‘y berubah secara langsung dengan x dan z’ ditulis sebagai y α xz.

3. ‘y berubah secara langsung dengan x dan secara songsang dengan z’ ditulis sebagai

y α \frac{x}{z} .

4. ‘y berubah secara songsang dengan x dan z’ ditulis sebagai

y α \frac{1}{x z} .

Contoh 1:

Cari hubungan bagi setiap ubahan yang berikut dengan menggunakan simbol ‘α’.

(a) x berubah secara langsung dengan y dan z.

(b) x berubah secara songsang dengan y dan

\sqrt{z} .

Penyelesaian:

\begin{array}{l} (a) x α y z \\ (b) x α \frac{1}{y \sqrt{z}} \\ (c) x α \frac{r^{3}}{y} \end{array}

(B) Menyelesaikan masalah yang melibatkan ubahan songsang

1. Jika

y α x^{n} z^{n}, maka y = k x^{n} z^{n}

, di mana k ialah pemalar dan n = 2, 3 dan ½.

2. Jika

y α \frac{1}{x^{n} z^{n}}, maka y = \frac{1}{k x^{n} z^{n}}

, di mana k ialah pemalar dan n = 2, 3 dan ½.

3. Jika

y α \frac{x^{n}}{z^{n}}, maka y = \frac{k x^{n}}{z^{n}}

, di mana k ialah pemalar dan n = 2, 3 dan ½.

Contoh 2:

Diberi bahawa

p α \frac{1}{q^{2} \sqrt{r}}

apabila p = 4, q = 2 and r = 16, hitungkan nilai r apabila p = 9 dan q = 4.

Penyelesaian:

\begin{array}{l} Diberi bahawa, \\ p α \frac{1}{q^{2} \sqrt{r}}, p = \frac{k}{q^{2} \sqrt{r}} \\ Apabila p = 4, q = 2 dan r = 16, \\ 4 = \frac{k}{2^{2} \sqrt{16}} \\ 4 = \frac{k}{16} \\ k = 64 \\ ∴ p = \frac{64}{q^{2} \sqrt{r}} \end{array}

\begin{array}{l} Apabila p = 9 dan q = 4, \\ 9 = \frac{64}{4^{2} \sqrt{r}} \\ 9 = \frac{4}{\sqrt{r}} \\ \sqrt{r} = \frac{4}{9} \\ r = {(\frac{4}{9})}^{2} = \frac{16}{81} \end{array}

Bab 16 Ubahan

Posted on May 12, 2016 by user

Soalan 6:

Diberi bahawa R berubah secara langsung dengan punca kuasa dua S dan secara songsang dengan kuasa dua T. Cari hubungan antara R, S dan T.

Penyelesaian:

R α \frac{\sqrt{S}}{T^{2}}

Soalan 7:

Diberi bahawa P berubah secara langsung dengan kuasa dua Q dan secara songsang dengan punca kuasa dua R. Diberi k ialah pemalar, Cari hubungan antara P, Qdan R.

Penyelesaian:

\begin{array}{l} P α \frac{Q^{2}}{\sqrt{R}} \\ P = \frac{k Q^{2}}{\sqrt{R}} \end{array}

Soalan 8:

Diberi bahawa P berubah secara songsang dengan punca kuasa tiga Q. Hubungan antara P dan Q ialah

Penyelesaian:

\begin{array}{l} P α \frac{1}{\sqrt[3]{Q}} \\ P α \frac{1}{Q^{\frac{1}{3}}} \end{array}

Soalan 9:

Diberi bahawa y berubah secara songsang dengan kuasa tiga x dan y = 16 apabila x = ½ . Ungkapkan y dalam sebutan x.

Penyelesaian:

\begin{array}{l} y α \frac{1}{x^{3}} \\ y = \frac{k}{x^{3}} \\ Apabila y = 16, x = \frac{1}{2} \end{array}

\begin{array}{l} 16 = \frac{k}{{(\frac{1}{2})}^{3}} \\ 16 = \frac{k}{\frac{1}{8}} \\ k = 2 \\ y = \frac{2}{x^{3}} \end{array}

Soalan 10:

W berubah secara langsung dengan X dan secara songsang dengan punca kuasa dua Y. Diberi k ialah pemalar, Cari hubungan antara W, Xdan Y.

Penyelesaian:

\begin{array}{l} W α \frac{X}{\sqrt{Y}} \\ W = \frac{k X}{\sqrt{Y}} \\ W = \frac{k X}{Y^{^{\frac{1}{2}}}} \end{array}