Bab 16 Ubahan

Posted on May 12, 2016 by user

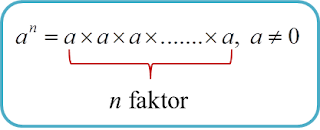
5.4 Ubahan, SPM Praktis (Soalan Pendek)

Soalan 1:

Diberi bahawa yberubah secara langsung dengan kuasa tiga xdan y = 192 apabila x = 4. Hitungkan nilai x apabila y = –24.

Penyelesaian:

y α x³

y = kx³

192 = k (4)³

k = 3

y = 3x³

Apabila y = – 24

–24 = 3x³

x = –2

Soalan 2:

Diberi bahawa yberubah secara langsung dengan kuasa dua xdan y = 9 apabila x = 2. Hitungkan nilai x apabila y = 16.

Penyelesaian:

y α x²

y = kx²

9 = k (2)

\begin{array}{l} k = \frac{9}{4} \\ y = \frac{9}{4} x^{2} \\ Apabila y = 16 \\ 16 = \frac{9}{4} x^{2} \\ x^{2} = \frac{64}{9} \\ x = \frac{8}{3} \end{array}

Soalan 3:

Diberi bahawa y berubah secara songsang w dan x dan y = 45 apabila w = 2 dan x = 1/6. Hitungkan nilai xapabila y = 15 dan w = ⅓

Penyelesaian:

\begin{array}{l} y α \frac{1}{w x} \\ y = \frac{k}{w x} \\ 45 = \frac{k}{(2) (\frac{1}{6})} \\ k = 45 \times \frac{1}{3} = 15 \\ y = \frac{15}{w x} \end{array}

\begin{array}{l} apabila y = 15, w = \frac{1}{3} \\ 15 = \frac{15}{(\frac{1}{3}) x} \\ \frac{x}{3} = 1 \\ x = 3 \end{array}

Soalan 4:

Diberi bahawa

p α \frac{1}{q \sqrt{r}}

dan p= 3 apabila q = 2 dan r = 16, cari nilai bagi p apabila q = 3 dan r = 4.

Penyelesaian:

\begin{array}{l} p α \frac{1}{q \sqrt{r}} \\ p = \frac{k}{q \sqrt{r}} \\ 3 = \frac{k}{(2) \sqrt{16}} \\ k = 24 \\ p = \frac{24}{q \sqrt{r}} \end{array}

\begin{array}{l} apabila q = 3, r = 4 \\ p = \frac{24}{3 \sqrt{4}} \\ p = \frac{24}{6} = 4 \end{array}

Soalan 5:

Diberi bahawa

P α \frac{1}{\sqrt{Q}} dan Q = 4 M + 1.

Jika P = 5 apabila M = 2, ungkapkan P dalam sebutan Q.

Penyelesaian:

\begin{array}{l} Diberi P α \frac{1}{\sqrt{Q}} \\ Maka, P = \frac{k}{\sqrt{Q}} \\ P = \frac{k}{\sqrt{4 M + 1}} \\ 5 = \frac{k}{\sqrt{4 (2) + 1}} \\ 5 = \frac{k}{\sqrt{9}} \\ k = 15 \\ P = \frac{15}{\sqrt{Q}} \end{array}

Bab 5 Indeks dan Logaritma

Posted on May 12, 2016 by user

5.2a Hukum-hukum Logaritma

\begin{array}{l} Hukum 1: \\ {log}_{a} x y = {log}_{a} x + {log}_{a} y \\ Contoh: \\ \log_{5} 25 x = {log}_{5} 25 + {log}_{5} x \\ Berhati-hati!! \\ {log}_{a} x + {log}_{a} y \neq {log}_{a} (x + y) \end{array}

\begin{array}{l} Hukum 2: \\ {log}_{a} (\frac{x}{y}) = {log}_{a} x - {log}_{a} y \\ Contoh: \\ \log_{5} \frac{x}{25} = {log}_{5} x - {log}_{5} 25 \\ Berhati-hati!! \\ {log}_{a} \frac{x}{y} \neq \frac{{log}_{a} x}{{log}_{a} y} \end{array}

\begin{array}{l} Hukum 3: \\ {log}_{a} x^{m} = m {log}_{a} x \\ Contoh: \\ \log_{5} y^{5} = 5 {log}_{5} y \\ Berhati-hati!! \\ {({log}_{a} x)}^{2} \neq 2 {log}_{a} x \end{array}

Contoh 1:

Ungkapkan setiap yang berikut dalam bentuk log_ax dan log_a y.

\begin{array}{l} (a) \log_{a} 3 x \\ (b) \log_{a} \frac{x}{5} \\ (c) \log_{a} y^{5} \\ (d) \log_{a} x y^{3} \\ (e) \log_{a} \frac{x^{2}}{\sqrt{5}} \\ (g) \log_{a} \sqrt{\frac{y}{a^{2} x^{3}}} \end{array}

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on May 11, 2016 by user

5.1 Indeks dan Hukum Indeks (Bahagian 2)

(C) Indeks Pecahan

\begin{array}{l} Secara amnya, bagi semua a . \\ a^{\frac{1}{n}} = \sqrt[n]{a} \\ a^{\frac{m}{n}} = \sqrt[n]{a^{m}} = {(\sqrt[n]{a})}^{m} \\ * \sqrt[n]{a} disebut punca kuasa n bagi a . \\ * {(\sqrt[n]{a})}^{m} disebut kuasa m bagi \\ punca kuasa n bagi a . \end{array}

Contoh 1:

Cari nilai-nilai yang berikut:

\begin{array}{l} {(a) 81}^{\frac{1}{2}} \\ {(b) 64}^{\frac{1}{3}} \\ {(c) 625}^{\frac{1}{4}} \end{array}

Penyelesaian:

\begin{array}{l} {(a) 81}^{\frac{1}{2}} = \sqrt{81} = 9 \\ {(b) 64}^{\frac{1}{3}} = \sqrt[3]{64} = 4 \\ {(c) 625}^{\frac{1}{4}} = \sqrt[4]{625} = 5 \end{array}

Contoh 2:

Cari nilai-nilai yang berikut:

\begin{array}{l} (a) 16^{\frac{3}{2}} \\ (b) {(\frac{27}{64})}^{\frac{2}{3}} \end{array}

Penyelesaian:

\begin{array}{l} (a) 16^{\frac{3}{2}} = {(16^{\frac{1}{2}})}^{3} = 4^{3} = 64 \\ (b) {(\frac{27}{64})}^{\frac{2}{3}} = {(\sqrt[3]{\frac{27}{64}})}^{2} = {(\frac{3}{4})}^{2} = \frac{9}{16} \end{array}

(D) Hukum-hukum Indeks

\begin{array}{l} a^{m} \times a^{n} = a^{m + n} \\ Contoh: \\ 3^{3} \times 3^{2} \\ = 3^{3 + 2} = 3^{5} = 243 \end{array}

\begin{array}{l} a^{m} \div a^{n} = a^{m - n} atau \frac{a^{m}}{a^{n}} = a^{m - n}, a \neq 0 \\ Contoh: \\ 3^{3} \div 3^{2} \\ = 3^{3 - 2} = 3^{1} = 3 \\ atau \\ \frac{3^{3}}{3^{2}} = 3^{3 - 2} = 3^{1} = 3 \end{array}

\begin{array}{l} {(a^{m})}^{n} = a^{m n} \\ Contoh: \\ {(7^{3})}^{4} = 7^{3 \times 4} = 7^{12} \end{array}

\begin{array}{l} {(a b)}^{n} = a^{n} b^{n} \\ Contoh: \\ {(15)}^{3} = {(5 \times 3)}^{3} = 2^{3} \times 3^{3} \end{array}

\begin{array}{l} {(\frac{a}{b})}^{n} = \frac{a^{n}}{b^{n}}, b \neq 0 \\ Contoh: \\ {(\frac{3}{5})}^{4} = \frac{3^{4}}{5^{4}} = \frac{81}{625} \end{array}

Bab 5 Indeks dan Logaritma

Posted on May 11, 2016 by user

Indeks Integer Positif

Jika a ialah suatu nombor dan n ialah suatu integer positif, maka aⁿbermakna pendaraban asas a sebanyak n kali dan disebut a kuasa n.

Integer n adalah indeks dan a ialah asasnya.

Contoh: 5×5×5×5 = 5⁴, 5 ialah asas dan 4 ialah indeks.

5.1 Indeks dan Hukum Indeks (Bahagian 1)

(A) Indeks Sifar

Indeks sifar bagi semua nombor adalah sama dengan satu.

a ^o = 1, di mana a ≠ 0

Contoh 1:

Cari nilai-nilai yang berikut:

(a) 250⁰

(b)0.513⁰

\begin{array}{l} (c) {(\frac{2}{7})}^{0} \\ (d) {(- 11 \frac{1}{25})}^{0} \end{array}

Penyelesaian:

(a) 250⁰ = 1

(b)0.513⁰ = 1

\begin{array}{l} (c) {(\frac{2}{7})}^{0} = 1 \\ (d) {(- 11 \frac{1}{25})}^{0} = 1 \end{array}

(B) Indeks Negatif

a^{- n} = \frac{1}{a^{n}}, n > 0

Contoh 2:

Cari nilai-nilai yang berikut:

(a) 102 ^-1

(b)–6 ^-3

\begin{array}{l} (c) {(\frac{1}{3})}^{- 4} \\ (d) {(\frac{2}{5})}^{- 2} \\ (e) - {(\frac{2}{5})}^{- 4} \end{array}

Penyelesaian:

\begin{array}{l} (a) 102^{- 1} = \frac{1}{102} \\ (b) - 6^{- 3} = \frac{1}{- 6^{3}} = - \frac{1}{216} \\ (c) {(\frac{1}{3})}^{- 4} = {(3)}^{4} = 81 \\ (d) {(\frac{2}{5})}^{- 2} = {(\frac{5}{2})}^{2} = \frac{25}{4} \\ (e) {(- \frac{2}{5})}^{- 4} = {(- \frac{5}{2})}^{4} = \frac{625}{16} \end{array}

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

Soalan 3:

Selesaikan persamaan serentak.

3y – 2x= – 4

y² + 4x² = 2

Penyelesaian:

3y – 2x= – 4 -----(1)

y² + 4x²= 2 -----(2)

\begin{array}{l} Dari (1), \\ y = \frac{2 x - 4}{3} ------- (3) \\ Gantikan (3) ke dalam (2), \\ {(\frac{2 x - 4}{3})}^{2} + 4 x^{2} = 2 \\ (\frac{4 x^{2} - 16 x + 16}{9}) + 4 x^{2} = 2 \\ 4 x^{2} - 16 x + 16 + 36 x^{2} = 18 (\times 9) \\ 40 x^{2} - 16 x - 2 = 0 \\ 20 x^{2} - 8 x - 1 = 0 \\ (10 x + 1) (2 x - 1) = 0 \\ x = - \frac{1}{10} atau x = \frac{1}{2} \\ Gantikan nilai-nilai x ke dalam (3), \\ Apabila x = - \frac{1}{10}, \\ y = \frac{2 (- \frac{1}{10}) - 4}{3} = - 1 \frac{2}{5} \\ Apabila x = \frac{1}{2}, \\ y = \frac{2 (\frac{1}{2}) - 4}{3} = - \frac{3}{3} = 1 \\ Penyelesaian ialah x = - \frac{1}{10}, y = - 1 \frac{2}{5} dan x = \frac{1}{2}, y = 1. \end{array}

Soalan 4:

Selesaikan persamaan serentak x – 3y = –1 dan y + yx– 2x = 0.

Beri jawapan anda betul kepada tiga tempat perpuluhan.

Penyelesaian:

x – 3y = –1 -----(1)

y + yx – 2x = 0 -----(2)

Dari (1),

x = 3y – 1 -----(3)

Gantikan (3) ke dalam (2),

y + y (3y – 1) – 2(3y – 1) = 0

y + 3y² – y – 6y+ 2 = 0

3y² – 6y + 2 = 0

\begin{array}{l} a = 3, b = - 6, c = 2 \\ y = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ y = \frac{- (- 6) \pm \sqrt{{(- 6)}^{2} - 4 (3) (2)}}{2 (3)} \\ y = \frac{6 \pm \sqrt{12}}{6} \\ y = 1.577 atau 0 .423 \end{array}

Gantikan nilai-nilai y ke dalam (3).

Apabila y = 1.577,

x = 3 (1.577) – 1 = 3.731 (tiga tempat perpuluhan)

Apabila y = 0.423,

x = 3 (0.423) – 1 = 0.269 (tiga tempat perpuluhan)

Penyelesaian ialah x = 3.731, y = 1.577 dan x = 0.269, y = 0.423.

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

4.2 SPM Praktis, Persamaan Serentak, (Soalan panjang)

Soalan 1:

Selesaikan persamaan serentak.

\begin{array}{l} y + 2 x = 2 \\ \frac{2}{x} + \frac{1}{y} = 5 \end{array}

Penyelesaian:

\begin{array}{l} y + 2 x = 2 - - - - (1) \\ \frac{2}{x} + \frac{1}{y} = 5 - - - - (2) \\ y = 2 - 2 x - - - - (3) \\ Gantikan (3) ke dalam (2), \\ \frac{2}{x} + \frac{1}{2 - 2 x} = 5 \\ \frac{2 (2 - 2 x) + x}{x (2 - 2 x)} = 5 \\ 4 - 4 x = 5 x (2 - 2 x) \\ 4 - 4 x = 10 x - 10 x^{2} \\ 10 x^{2} - 14 x + 4 = 0 \\ 5 x^{2} - 7 x + 2 = 0 \\ (5 x - 2) (x - 1) = 0 \\ 5 x - 2 = 0 or x - 1 = 0 \\ x = \frac{2}{5} or x = 1 \\ Gantikan nilai-nilai x ke dalam (3), \\ Apabila x = \frac{2}{5}, \\ y = 2 - 2 (\frac{2}{5}) = 1 \frac{1}{5} \\ Apabila x = 1 \\ y = 2 - 2 (1) = 0 \\ Penyelesaian ialah x = \frac{2}{5}, y = 1 \frac{1}{5} dan x = 1, y = 0 \end{array}

Soalan 2:

Selesaikan persamaan serentak.

x – 3y + 5 = 3y + 5y²– 6 – x = 0

Penyelesaian:

x – 3y + 5 = 0

x = 3y – 5 -----(1)

3y + 5y² – 6 – x = 0 -----(2)

Gantikan (1) ke dalam (2),

3y + 5y² – 6 – (3y – 5) = 0

3y + 5y² – 6 – 3y + 5 = 0

5y² – 1 = 0

5y² = 1

y = 0.447

Gantikan nilai-nilai yke dalam (1),

Apabila y = 0.447

x = 3 (0.447) – 5

x = –3.659

Apabila y = – 0.447

x = 3 (–0.447) – 5

x = –6.341

Penyelesaian ialah x = –3.659, y = 0.447 dan x = –6.341, y = – 0.447.

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

4.1 Persamaan Serentak (contoh 1 & 2)

Contoh 1:

Selesaikan persamaan serentak,

x + \frac{1}{4} y = 1 dan y^{2} - 8 = 4 x .

Penyelesaian:

\begin{array}{l} x + \frac{1}{4} y = 1 \to (1) \\ y^{2} - 8 = 4 x \to (2) \\ x = 1 - \frac{1}{4} y \to (3) \end{array}

\begin{array}{l} Gantikan (3) ke dalam (2), \\ y^{2} - 8 = 4 (1 - \frac{1}{4} y) \\ y^{2} - 8 = 4 - \frac{4}{4} y \\ y^{2} + y - 12 = 0 \\ (y + 4) (y - 3) = 0 \\ y = - 4 atau y = 3 \end{array}

\begin{array}{l} Gantikan nilai-nilai y ke dalam (3), \\ apabila y = - 4, \\ x = 1 - \frac{1}{4} (- 4) = 2 \\ apabila y = 3, \\ x = 1 - \frac{1}{4} (3) = \frac{1}{4} \end{array}

Penyelesaian ialah x = 2, y = –4 dan x = ¼, y = 3.

Contoh 2:

Selesaikan persamaan serentak 2x + y = 1 dan 2x² + y² + xy = 5.

Beri jawapan anda betul kepada tiga tempat perpuluhan.

Penyelesaian:

2x + y = 1-----(1)

2x²+ y² + xy = 5-----(2)

Dari (1),

y= 1 – 2x-----(3)

Gantikan (3) ke dalam (2).

2x²+ (1 – 2x)² + x(1 – 2x) = 5

2x²+ (1 – 2x)(1 – 2x) + x – 2x² = 5

1 – 2x – 2x + 4x²+ x – 5 = 0

4x²– 3 x – 4 = 0

\begin{array}{l} Dari x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ a = 4, b = - 3, c = - 4 \\ x = \frac{- (- 3) \pm \sqrt{{(- 3)}^{2} - 4 (4) (- 4)}}{2 (4)} \\ x = \frac{3 \pm \sqrt{73}}{8} \\ x = - 0.693 or 1.443 \end{array}

Gantikan nilai-nilai x ke dalam (3).

Apabila x= –0.693,

y = 1 – 2 (–0.693) = 2.386 (tiga tempat perpuluhan)

Apabila x= 1.443,

y = 1 – 2 (1.443) = –1.886 (tiga tempat perpuluhan)

Penyelesaian ialah x = –0.693, y = 2.386 dan x = 1.443, y = –1.886.

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

4.1 Persamaan Serentak

(A) Langkah-langkah penyelesaian persamaan serentak:

Susun persamaan linear supaya satu daripada anu-anu itu menjadi perkara rumus bagi persamaan itu.
Gantikan persamaan linear ke dalam persamaan tak linear.
Permudahkan dan ungkapkan persamaan yang diperoleh daripada langkah kedua dalam bentuk am persamaan kuadratik ax² + bx + c = 0

Selesaikan persamaan kuadratik.
Cari nilai anu yang kedua dengan menggantikan nilai anu pertama yang diperolehi ke dalam persamaan linear.

Contoh:

Selesaikan persamaan serentak.

y + x = 9

xy = 20

Penyelesaian:

Langkah1: Susun persamaan linear supaya satu daripada anu itu menjadi perkara rumus bagi persamaan itu

y + x = 9 ---- (1)

xy = 20 ---- (2)

y = 9 – x ----(3)

Langkah 2: Gantikan persamaan linear (persamaan (3) dari langkah (1) ke dalam persamaan tak linear.

xy = 20

x (9 – x) = 20

9x – x² = 20

Langkah 3: Permudahkan dan ungkapkan persamaan yang diperoleh daripada langkah 2 dalam bentuk am persamaan kuadratik ax² + bx + c = 0

9x – x² = 20

x² – 9x+ 20 = 0

Langkah 4:Selesaikan persamaan kuadratik.

x² – 9x+ 20 = 0

(x – 4) (x – 5) = 0

x = 4 or x = 5

Langkah 5:Cari nilai anu yang kedua dengan menggantikan nilai anu pertama yang diperolehi ke dalam persamaan linear.

Apabila x = 4,

y = 9 – x

y = 9 – 4 = 5

Apabila x = 5,

y = 9 – x

y = 9 – 5 = 4

Penyelesaian ialah x = 4, y = 5 dan x = 5, y = 4.

Bab 5 Garis Lurus

Posted on May 9, 2016 by user

5.5 Garis Selari (Bhg 1)

(A) Kecerunan Garis Selari

1. Dua garis adalah selari jika kecerunannya adalah sama.

Jika PQ // RS,

maka m_PQ= m_RS

2. Jika dua garis lurus mempunyai kecerunan yang sama, maka pasangan garis lurus tersebut adalah selari.

Jika m_AB= m_CD

maka AB // CD

Contoh 1:

Tentukan sama ada setiap pasangan garis lurus berikut adalah selari atau tidak.

(a) 2y – 4x = 6

y = 2x – 5

(b) 2y = 3x – 4

3y = 2x + 12

Penyelesaian:

(a)

2y – 4x = 6

2y = 6 + 4x

y = 2x + 3, m₁= 2

y = 2x – 5, m₂ = 2

m₁= m₂

Maka, dua garis lurus adalah selari.

(b)

\begin{array}{l} 2 y = 3 x - 4 \\ y = \frac{3}{2} x - 2, m_{1} = \frac{3}{2} \\ 3 y = 2 x + 12 \\ y = \frac{2}{3} x + 4, m_{2} = \frac{2}{3} \\ m_{1} \neq m_{2} \\ ∴ Maka, dua garis lurus adalah tidak selari . \end{array}

Bab 5 Garis Lurus

Posted on May 9, 2016 by user

5.3 Pintasan

1. Pintasan-x ialah koordinat-xbagi titik persilangan suatu garis lurus dengan paksi-x.

2. Pintasan-y ialah koordinat-ybagi titik persilangan suatu garis lurus dengan paksi-y.

3. Dalam rajah di atas, pintasan-x bagi garis lurus PQ ialah 6 dan pintasan-y bagi PQ ialah 5.

4. Jika pintasan-x dan pintasan-y diberikan,

Kecerunan, m = - \frac{Pintasan- y}{Pintasan- x}