2.1.1 The Human Skeleton

Posted on May 4, 2016 by user

The Human Skeleton

1. Human skeleton consists of two main parts: axial skeleton and appendicular skeleton.
2. The axial skeleton consists of the skull, vertebral column, ribs and sternum.

Skull

Ribs and the sternum

Vertebral column

Cervical vertebrae

Thoracic vertebrae

Lumbar vertebrae

Bab 1 Bentuk Piawai

Posted on May 4, 2016 by user

1.1 Angka Bererti

Angka Bererti (Bahagian 1)

1. Angka bererti merujuk kepada digit-digit yang relevan dalam sesuatu integer atau perpuluhan yang dihampirkan kepada sesuatu nilai mengikut tahap kejituan yang tertentu.

2. Semasa membundarkan suatu nombor positif kepada bilangan angka bererti, peranan sifar ditunjukkan seperti berikut.

(a) Semua digit bukan sifar dalam suatu nombor adalah angka bererti.

Contoh:

(i) 568 (3 angka bererti)

(ii) 36.97 (4 angka bererti)

(b) Sifar yang terletak di antara digit-digit bukan sifar adalah angka bererti.

Contoh:

(i) 7001 (4 angka bererti)

(ii) 3.04 (4 angka bererti)

(iii) 22.054 (4 angka bererti)

(c) Sifar yang terletak di sebelah kanan digit bukan sifar dalam suatu berpuluhan adalah angka bererti.

Contoh:

(i) 0.70 (2 angka bererti)

(ii) 4.500 (4 angka bererti)

(iii) 3.00 (3 angka bererti)

(d) Sifar yang terletak di sebelah kiri digit bukan sifar dalam suatu berpuluhan kurang daripada 1 adalah bukan angka bererti.

Contoh:

(i) 0.05 (1 angka bererti)

(ii) 0.0040 (2 angka bererti)

(iii) 0.07040 (4 angka bererti)

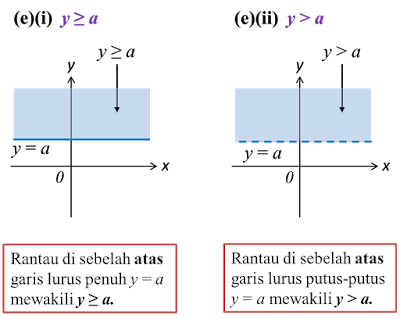
(e) Sifar di hujung suatu nombor bulatdianggap sebagai bukan angka berertikecuali dinyatakan.

Contoh:

(i) 40 (1 angka bererti)

(ii) 3670 (3 angka bererti)

(iii) 704200 (4 angka bererti)

Contoh 1:

Bundarkan setiap nombor yang berikut betul kepada tiga angka bererti.

(a) 246= 246 (3 angka bererti)

(b) 2463 = 2460 (3 angka bererti)

(d) 0.00745= 0.00745 (3 angka bererti)

(e) 0.007453 = 0.00745 (3 angka bererti)

(f) 0.007455 = 0.00746 (3 angka bererti)

(g) 0.007403 = 0.00740 (3 angka bererti)

Contoh 2:

Bundarkan setiap nombor yang berikut betul kepada bilangan angka bererti yang ditunjukkan dalam kurungan, [ ].

(a) 3548 (2 angka bererti)

(b) 0.5089 (3 angka bererti)

(d) 0.40055 (3 angka bererti)

(e) 0.681 (2 angka bererti)

(f) 38.97 (3 angka bererti)

Penyelesaian:

(a) 3500 (2 angka bererti)

(b) 0.509 (3 angka bererti)

(d) 0.401 (3 angka bererti)

(e) 0.68 (2 angka bererti)

(f) 39.0 (3 angka bererti)

Bab 8 Bulatan III

Posted on May 4, 2016 by user

8.3 Tangen Sepunya

Tangen sepunya kepada dua bulatan ialah suatu garis lurus yang menyentuh kedua-dua bulatan itu masing-masing pada satu titik sahaja.

1. Bersilang di dua titik
(a) Bulatan sama saiz

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Dua tangen sepunya: AB dan CD	AC = BD AB = CD AB selari dengan OR selari dengan CD

(b) Bulatan saiz berbeza

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Dua tangen sepunya: ABE dan CDE	AB = CD BE = DE OA // RB OC // RD

2. Bersilang di satu titik
(a) Bulatan sama saiz

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Tiga tangen sepunya: AB, CD dan PQ	AC = PQ = BD AB = OR = CD AB // OR // CD AC // PQ // BD PQ berserenjang dengan OR

(b) Bulatan saiz berbeza
(i) Bersentuh di luar bulatan

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Tiga tangen sepunya: ABE, CDE dan PQ	AB = CD BE = DE OA // RB OC // RD PQ berserenjang dengan ORE

(ii) Bersentuh di dalam bulatan

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Satu tangen sepunya: PQR	ONQ berserenjang dengan PR

3. Tidak bersilang

(a) Bulatan sama saiz

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Empat tangen sepunya: AB, CD, PS and RQ	AB = CD = OV PS = RQ AB // OV // CD

(b) Bulatan saiz berbeza

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Empat tangen sepunya: AB, CD, PS dan RQ	AB = CD BT = DT PS = RQ OA // VB OC // VD

Bab 8 Bulatan III

Posted on May 4, 2016 by user

8.2.1 Sudut di antara Tangen dengan Perentas (Contoh Soalan)

Contoh 2:

Dalam rajah, PQR ialah tangen kepada bulatan QSTU di titik Q.

Cari nilai bagi y.

Penyelesaian:

∠QUT = 180^o– 98^o ← (sudut bertentangan dalam sisi empat kitaran QSTU)

= 82^o

∠QTU = 75^o ← (sudut dalam tembereng selang-seli)

Oleh itu y = 180^o – (82^o + 75^o) ← (Jumlah sudut dalaman ∆ QTU)

= 23^o

Contoh 3:

Dalam rajah, PQR ialah tangen kepada bulatan QSTU di titik Q.

Cari nilai bagi
(a) x
(b) y

Penyelesaian:

(a)

∠UTS + ∠UQS = 180^o ← (sudut bertentangan dalam sisi empat kitaran QSTU)

105^o + ∠UQS = 180^o

∠UQS = 75^o

x + 75^o + 20^o = 180^o ← (Jumlah sudut garis lurus PQR = 180^o)

x + 95^o = 180^o

x = 85^o

(b)

∠PQU = ∠QSU ← (sudut dalam tembereng selang-seli)

85^o = 35^o + y

y = 50^o

Contoh 4:

Dalam rajah, ABC ialah tangen kepada bulatan BDE dengan pusat O, di titik B.

Cari nilai bagi x.

Penyelesaian:

\begin{array}{l} ∠ B E D = ∠ C B D = 54^{\circ} \\ ∠ B D E \\ = \frac{180^{\circ} - 54^{\circ}}{2} = 63^{\circ} \leftarrow \begin{array}{l} Segi tiga kaki sama \\ ∠ E B D = ∠ E D B \end{array} \end{array}

∠ABE = ∠BDE = 63^o

Dalam ∆ABE,

x^o+ 45^o+ 63^o= 180^o

x^o+ 108^o= 180^o

x = 72

Bab 8 Bulatan III

Posted on May 4, 2016 by user

8.2 Sudut di antara Tangen dengan Perentas

1. Dalam rajah, ABC ialah tangen kepada bulatan di titik B.

2. Perentas PB membahagikan bulatan kepada dua tembereng, iaitu tembereng minor PRB dan tembereng major PQB.

3. Sudut dalam tembereng selang-seli yang dicangkum oleh perentas PB yang melalui titik sentuhan tangen ialah ∠BQP.

4. Manakala, sudut dalam tembereng selang-seli yang dicangkum oleh perentas BQ yang melalui titik sentuhan tangen ialah ∠BPQ.

5. Sudut di antara tangen dengan perentas yang melalui titik sentuhan tangen adalah sama dengan sudut dalam tembereng selang-seli yang dicangkum oleh perentas itu.

6. Hubungan antara sudut-sudut adalah berikut:

∠ ABP = ∠ BQP

∠ CBQ = ∠ BPQ

Contoh 1:

Dalam rajah di atas, ABC ialah tangen kepada bulatan BDE di titik B.

Panjang lengkok BD adalah sama dengan panjang lengkok DE.

Cari nilai bagi p.

Penyelesaian:

∠BED = 82^o ← (sudut dalam tembereng selang-seli)

∠DBE = 82^o ← (Lengkok BD = Lengkok DE, BDE ialah segi tiga kaki sama)

Oleh itu p= 180^o – 82^o – 82^o

= 16^o

Bab 8 Bulatan III

Posted on May 3, 2016 by user

8.1 Tangen kepada Bulatan

1. Tangen kepada bulatan ialah garis lurus yang menyentuh bulatan itu pada satu titik sahaja. Titik tersebut dipanggil titik sentuhan.

2. Jejari yang melalui titik sentuhan tangen adalah berserenjang dengan tangen itu.

Jika ABC ialah tangen kepada bulatan di B, maka ∠ABO = ∠CBO = 90^o.

8.1.1 Sifat-sifat Berkaitan dengan Dua Tangen kepada Suatu Titik di Luar Bulatan

Dalam rajah di atas, BA dan BC ialah dua tangen dari satu titik luar B. Sifat-sifat bagi tangennya adalah berikut.

\begin{array}{l} (a) B A = B C \\ (b) ∠ A B O = ∠ C B O = x^{o} \\ (c) ∠ A O B = ∠ C O B = y^{o} \\ (d) ∠ O A B = ∠ O C B = 90^{o} \\ (e) ∠ A O C + ∠ A B C = 180^{o} \\ (f) Δ A O B dan Δ C O B adalah kongruen \end{array}

Contoh 1:

Rajah di atas menunjukkan sebuah bulatan dengan pusat O. ABC dan CDE ialah dua tangen kepada bulatan di titik B dan D masing-masing. Cari panjang OC

Penyelesaian:

OC²= OB² + BC² ← (Teori Pythagoras)

= 6²+ 8²

= 100

OC = √100 = 10 cm

Contoh 2:

Dalam rajah di atas, AB dan BC ialah dua tangen kepada bulatan dengan pusat O. Hitung nilai bagi
(a) x (b) y

Penyelesaian:

(a) AB = BC

7 + x = 12

x = 5

(b)

∠OBA = ∠OCB = 21^o

∠OCB = 90^o← (OC berserenjang dengan CB)

y^o= 180^o– 21^o– 90^o

y = 69

Contoh 3:

Dalam rajah di atas, ABC ialah tangen kepada bulatan dengan pusat O di titikt B. CDE ialah garis lurus. Cari nilai bagi x.

Penyelesaian:

∠CBO = 90^o← (OB berserenjang dengan BC)

Dalam ∆ BCE,

x^o= 180^o– 30^o– 50^o – 90^o

x = 10^o

Bab 13 Garf Fungsi II

Posted on May 3, 2016 by user

2.1 Graf Fungsi (Bahagian 1)

(A) Melukis graf fungsi

1. Langkah-langkah berikut diambil untuk melukis sebuah graf fungsi yang diberikan.

Langkah 1: Membina satu jadual nilai bagi fungsi yang diberikan.

Langkah 2: Memilih skala yang sesuai bagi paksi-x dan paksi-y, jika ia tidak diberikan.

Langkah 3: Plotkan titik-titik dan melengkapkan graf dengan menyertai titik-titik itu.

Langkah 4: Melabelkan graf.

Bab 13 Garf Fungsi II

Posted on May 3, 2016 by user

2.3 Rantau yang Mewakili Ketaksamaan dalam Dua Pemboleh Ubah

2.3.1 Menentukan kedudukan suatu titik relative kepada graf y= ax + b

1.Apabila y = ax + b, titik terletak pada garis.

2.Apabila y < ax + b, titik terletak di sebelah bawah garis.

3.Apabila y > ax + b, titik terletak di sebelah atas garis.

2.3.2 Mengenal pasti rantau yang memuaskan ketaksamaan linear serentak.

1. Garis putus-putus ‘----’ dilukis apabila semua titik pada garis adalah tidak termasuk dalam rantau yang mewakili ketaksamaan itu, contohnya y > ax + b atau y < a atau x > a.

2. Garis penuh ‘ ___’ dilukis apabila semua titik pada garis adalah termasukdalam rantau yang mewakili ketaksamaan itu, contohnya y ≥ ax + b atau y ≤ a atau x ≥ a.

3. Gambar rajah di bawah menunjukkan rantau-rantau yang mewakili ketaksamaan masing-masing.

Bab 13 Garf Fungsi II

Posted on May 2, 2016 by user

2.3.3 Rantau yang Mewakili Ketaksamaan dalam Dua Pemboleh Ubah (Contoh Soalan)

Soalan 1:

Pada graf di ruang jawapan, lorekkan rantau yang memuaskan ketiga-tiga ketaksamaan y ≥ –x + 10, y > x dan y < 9.

Jawapan:

Penyelesaian:

1. Rantau yang mewakili ketaksamaan y ≥ –x + 10 adalah rantau yang terletak pada serta di sebelahatas garis y = –x + 10.

2. Rantau yang mewakili ketaksamaan y > x adalah rantau yang terletak di sebelah atas garis y = x. Oleh kerana symbol ketaksamaan “>” digunakan, maka semua titik pada garis y = x adalah dikecualikan dalam rantau. Akibatnya, y = x dilukis dengan satu garis putus-putus.

3. Rantau yang mewakili ketaksamaan y < 9 adalah rantau yang terletak di sebelah bawahgaris y = 9 yang dilukis dengan garis putus-putus.

Soalan 2:

Pada graf di ruang jawapan, lorekkan rantau yang memuaskan ketiga-tiga ketaksamaan y ≥ –2x + 10, y ≤ 10 dan x < 5.

Jawapan:

Penyelesaian:

1. Rantau yang mewakili ketaksamaan y ≥ ax + cadalah rantau yang terletak pada serta di sebelah atas garis y = ax + c.

2. Dalam soalan ini, pintasan-y, c = 10, pintasan-x ialah 5.

3. Rantau yang mewakili ketaksamaan y ≥ –2x + 10 adalah rantau yang terletak pada serta di sebelah atasgaris y = –2x + 10.

4. Rantau yang mewakili ketaksamaan y ≤ 10 adalah rantau yang terletak pada serta di sebelah bawah garis y = 10.

5. Rantau yang mewakili ketaksamaan x < 5 terletak pada sebelah kiri garis x = 5 yang dilukis dengan garis putus-putus.

Bab 13 Garf Fungsi II

Posted on May 2, 2016 by user

Soalan 3:

(a) Jadual di bawah menunjukkan nilai-nilai x dan y bagi persamaan y = –x³+ 3x + 1.

Hitung nilai r dan nilai s.

(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.

Dengan menggunakan skala 2cm kepada 1 unit pada paksi-x dan 2 cm kepada 5 unit pada paksi-y, lukis graf y = –x³ + 3x + 1 for –3 ≤ x ≤ 4 dan –51 ≤ y ≤ 19.

(c) Daripada graf anda, cari
(i) nilai y apabila x = –2.8,
(ii) nilai x apabila y = –30.

(d) Lukis satu garis lurus yang sesuai pada graf anda untuk mencari nilai-nilai x yang memuaskan persamaan –x³ + 13x – 9 = 0 bagi –3 ≤ x ≤ 4 dan –51 ≤ y ≤ 19.

Penyelesaian:

(a)

y = –x³ + 3x + 1

apabila x = –1,

r = – (–1)³ + 3(–1) + 1

= 1 – 3 + 1 = –1

apabila x = 3,

s = – (3)³ + 3(3) + 1 = –17

(b)

(c)

(i) Dari graf, apabila x = –2.8, y = 15

(ii) Dari graf, apabila y = –30, x = 3.5

(d)

y = –x³ + 3x + 1 ----- (1)

–x³+ 13x – 9 = 0 ----- (2)

y = –x³ + 3x + 1 ----- (1)

0 = –x³+ 13x – 9 ------ (2) ← (Menyusun semula (2))

(1) – (2) : y = –10x + 10

Garis lurus yang sesuai ialah y = –10x + 10.

Menentukan koordinat-x bagi titik-titik persilangan antara lengkungan y = –x³+ 3x + 1 dan garis lurus y = –10x + 10.

x	0	4
y = –10x + 10	10	–30

Dari graf, x = 0.7, 3.25.

Soalan 4:
(a) Lengkapkan jadual di ruang jawapan bagi persamaan y = x³ – 4x – 10 dengan menulis nilai-nilai y apabila x = –1 dan x = 3.

(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Dengan menggunakan skala 2cm kepada 1 unit pada paksi-x dan 2 cm kepada 10 unit pada paksi-y, lukis graf y = x³ – 4x – 10 untuk –3 ≤ x ≤ 4 dan –25 ≤ y ≤ 38.

(c) Dari graf, cari,
(i) nilai y apabila x = 2.2,
(ii) nilai x apabila y = 15.

(d) Lukis satu garis lurus yang sesuai pada graf anda untuk mencari nilai-nilai x yang memuaskan persamaan x³ – 12x – 5 = 0 untuk –3 ≤ x ≤ 4 dan –25 ≤ y ≤ 38.

Jawapan:

Penyelesaian:
(a)
y = x³ – 4x – 10
Apabila x = –1,
y = (–1)³ – 4(–1) – 10
= –7

Apabila x = 3,
y = (3)³ – 4(3) – 10
= 5

(b)

(c)
(i) Dari graf, apabila x = 2.2, y = –8
(ii) Dari graf, apabila y = 15, x = 3.4

(d)
y = x³ – 4x – 10 ----- (1)
0 = x³ – 12x – 5 ----- (2)
(1) – (2) : y = 8x – 5
Garis lurus yang sesuai ialah y = 8x–5.

Menentukan koordinat-x bagi titik-titik persilangan antara lengkungan y = x³ – 4x – 10 dan garis lurus y = 8x –5.

x	0	2
y = 8x – 5	–5	–11

Dari graf, x = –0.45, 3.7.