Bab 14 Pengamiran

Posted on May 16, 2016 by user

3.7 Pengamiran, SPM Praktis (Kertas 1)

Soalan 2:

Diberi bahawa

\int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c,

Cari nilai-nilai mdan n.

Penyelesaian:

\begin{array}{l} \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c \\ \int 4 {(1 + x)}^{- 4} d x = m {(1 + x)}^{n} + c \\ \frac{4 {(1 + x)}^{- 3}}{- 3 (1)} + c = m {(1 + x)}^{n} + c \\ - \frac{4}{3} {(1 + x)}^{- 3} + c = m {(1 + x)}^{n} + c \\ m = - \frac{4}{3}, n = - 3 \end{array}

Soalan 3:

Diberi

\int_{- 1}^{2} 2 g (x) d x = 4, dan \int_{- 1}^{2} [m x + 3 g (x)] d x = 15.

Cari nilai pemalar m.

Penyelesaian:

\begin{array}{l} \int_{- 1}^{2} [m x + 3 g (x)] d x = 15 \\ \int_{- 1}^{2} m x d x + \int_{- 1}^{2} 3 g (x) d x = 15 \\ {[\frac{m x^{2}}{2}]}_{- 1}^{2} + 3 \int_{- 1}^{2} g (x) d x = 15 \\ [\frac{m {(2)}^{2}}{2} - \frac{m {(- 1)}^{2}}{2}] + \frac{3}{2} \int_{- 1}^{2} 2 g (x) d x = 15 \\ 2 m - \frac{1}{2} m + \frac{3}{2} (4) = 15 \leftarrow diberi \int_{- 1}^{2} 2 g (x) d x = 4 \\ \frac{3}{2} m + 6 = 15 \\ \frac{3}{2} m = 9 \\ m = 9 \times \frac{2}{3} \\ m = 6 \end{array}

Soalan 4:

Diberi

\frac{d}{d x} (\frac{2 x}{3 - x}) = g (x), cari \int_{1}^{2} g (x) d x .

Penyelesaian:

\begin{array}{l} Diberi \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x) \\ \int g (x) d x = \frac{2 x}{3 - x} \\ dengan itu, \\ \int_{1}^{2} g (x) d x = {[\frac{2 x}{3 - x}]}_{1}^{2} \\ = \frac{2 (2)}{3 - 2} - \frac{2 (1)}{3 - 1} \\ = 4 - 1 \\ = 3 \end{array}

Bab 14 Pengamiran

Posted on May 16, 2016 by user

3.7 Pengamiran, SPM Praktis (Kertas 1)

Soalan 1:

Kamirkan setiap yang berikut terhadap x.

\begin{array}{l} (a) \int (\frac{3}{x^{2}} - \frac{5}{2 x^{3}} + 2) d x \\ (b) \int x^{2} (x^{5} + 2 x) d x \\ (c) \int \frac{3 x^{4} + 2 x}{x^{3}} d x \\ (d) \int \frac{(7 + x) (7 - x)}{x^{4}} d x \\ (e) \int {(5 x - 1)}^{3} d x \\ (f) \int \frac{3}{{(4 x + 7)}^{8}} d x \end{array}

Penyelesaian:

\begin{array}{l} (a) \\ \int (\frac{3}{x^{2}} - \frac{5}{2 x^{3}} + 2) d x \\ = \int (3 x^{- 2} - \frac{5 x^{- 3}}{2} + 2) d x \\ = - 3 x^{- 1} + \frac{5 x^{- 2}}{4} + 2 x + c \\ = - \frac{3}{x} + \frac{5}{4 x^{2}} + 2 x + c \end{array}

\begin{array}{l} (b) \\ \int x^{2} (x^{5} + 2 x) d x \\ = \int (x^{7} + 2 x^{3}) d x \\ = \frac{x^{8}}{8} + \frac{2 x^{4}}{4} + c \\ = \frac{x^{8}}{8} + \frac{x^{4}}{2} + c \end{array}

\begin{array}{l} (c) \\ \int \frac{3 x^{4} + 2 x}{x^{3}} d x \\ = \int (\frac{3 x^{4}}{x^{3}} + \frac{2 x}{x^{3}}) d x = \int (3 x + 2 x^{- 2}) d x \\ = \frac{3 x^{2}}{2} - \frac{2}{x} + c \end{array}

\begin{array}{l} (d) \\ \int \frac{(7 + x) (7 - x)}{x^{4}} d x = \int (\frac{49 - x^{2}}{x^{4}}) d x \\ = \int (\frac{49}{x^{4}} - \frac{1}{x^{2}}) d x = \int (49 x^{- 4} - x^{- 2}) d x \\ = \frac{49 x^{- 3}}{- 3} + \frac{1}{x} + c \\ = - \frac{49}{3 x^{3}} + \frac{1}{x} + c \end{array}

\begin{array}{l} (e) \\ \int {(5 x - 1)}^{3} d x \\ = \frac{{(5 x - 1)}^{4}}{(4) (5)} + c \\ = \frac{1}{20} {(5 x - 1)}^{4} + c \end{array}

\begin{array}{l} (f) \\ \int \frac{3}{{(4 x + 7)}^{8}} d x = \int 3 {(4 x + 7)}^{- 8} d x \\ = \frac{3 {(4 x + 7)}^{- 7}}{(- 7) (4)} + c \\ = - \frac{3}{28 {(4 x + 7)}^{7}} + c \end{array}

Bab 12 Janjang

Posted on May 16, 2016 by user

1.3 Janjang, SPM Praktis (Soalan Pendek)

Soalan 1:

Tiga sebutan pertama bagi suatu janjang aritmetik ialah 2k, 3k + 3, 5k + 1. Cari

(a) nilai k.

(b) hasil tambah 15 sebutan pertama janjang aritmetik itu.

Penyelesaian:

(a)

2k, 3k + 3, 5k + 1 ← (Jika a, b, cialah 3 sebutan berturutan dalam suatu janjang aritmetik, c – b = b – a)

(5k + 1) – (3k + 3) = (3k + 3) – 2k

2k – 2 = k + 3

k= 5

(b)

2(5), 3(5) + 3, 5(5) + 1

10, 18, 26

a = 10, d = 18 – 10 = 8

\begin{array}{l} S_{15} = \frac{15}{2} [2 (10) + 14 (8)] \\ = \frac{15}{2} (132) = 990 \end{array}

Soalan 2:

Diberi suatu janjang aritmetik ialah p + 9, 2p + 10, 7p – 1,…., dengan keadaan p ialah satu pemalar. Cari

(a) nilai p.

(b) hasil tambah 5 sebutan seterusnya.

Penyelesaian:

(a)

p+ 9, 2p + 10, 7p – 1

(7p – 1) – (2p + 10) = (2p + 10) – (p + 9)

5p – 11 = p + 1

4p = 12

p = 3

(b)

3 + 9, 2(3) + 10, 7(3) – 1

12, 16, 20, (5 sebutan seterusnya), …

a= 12, d = 16 – 12 = 4

Hasil tambah 5 sebutan seterus

= S₈– S₃

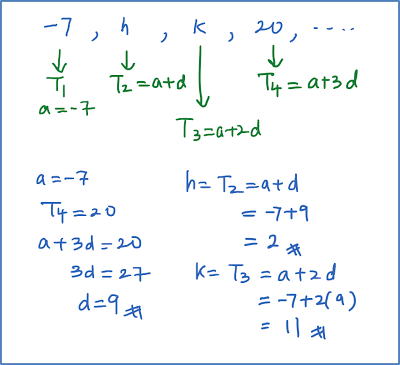
\begin{array}{l} = \frac{8}{2} [2 (12) + 7 (4)] - (12 + 16 + 20) \\ = 208 - 48 \\ = 160 \end{array}

Soalan 3:

Diberi bahawa –7, h, k, 20, …, adalah empat sebutan pertama bagi suatu janjang aritmetik. Cari nilai h dan k.

Penyelesaian:

Bab 12 Janjang

Posted on May 16, 2016 by user

1.3 Janjang, SPM Praktis (Soalan Pendek)

Soalan 4:

Sebutan keempat suatu janjang geometri ialah –20. Hasil tambah sebutan keempat dan kelima ialah –16.

Cari sebutan pertama dan nisbah sepunya janjang itu.

Penyelesaian:

T₄ = –20

ar³ = –20 ---- (1) ← (T_n= ar^n–1)

T₄ + T₅ = –16

–20 + T₅= –16

T₅ = 4

ar⁴ = 4 ---- (2)

\begin{array}{l} \frac{(2)}{(1)} \frac{a r^{4}}{a r^{3}} = \frac{4}{- 20} \\ r = - \frac{1}{5} \\ Gantikan r = - \frac{1}{5} ke dalam (1) \\ a {(- \frac{1}{5})}^{3} = - 20 \\ a = 2500 \end{array}

Soalan 5:

Bagi suatu janjang geometri, hasil tambah dua sebutan pertama ialah 30 dan sebutan ketiga melebehi sebutan pertama sebanyak 15 .

Cari sebutan pertama dan nisbah sepunya janjang itu.

Penyelesaian:

T₁ + T₂ = 30

a + ar= 30

a (1 +r) = 30 ---- (1)

T₃ – T₁ = 15

ar² – a = 15

a (r² – 1) = 15 ---- (2)

\begin{array}{l} \frac{(2)}{(1)} \frac{a (r^{2} - 1)}{a (1 + r)} = \frac{15}{30} \\ \frac{(r - 1) (r + 1)}{1 + r} = \frac{1}{2} \to \begin{array}{l} (r^{2} - 1) = \\ (r - 1) (r + 1) \end{array} \\ r - 1 = \frac{1}{2} \\ r = \frac{1}{2} + 1 = \frac{3}{2} \\ Dari (1), a (1 + r) = 30 \\ a (1 + \frac{3}{2}) = 30 \\ \frac{5 a}{2} = 30 \\ a = 12 \end{array}

Soalan 6:

Hasil tambah nsebutan pertama bagi suatu janjang geometri 5, 15, 75, …., ialah 5465.

Cari nilai n.

Penyelesaian:

\begin{array}{l} a = 5, r = \frac{15}{5} = 3 \\ S_{n} = 5465 \to S_{n} = \frac{a (r^{n} - 1)}{r - 1}, r > 1 \\ \frac{5 (3^{n} - 1)}{3 - 1} = 5465 \\ 3^{n} - 1 = \frac{10930}{5} \\ 3^{n} - 1 = 2186 \\ 3^{n} = 2187 \\ 3^{n} = 3^{7} \\ n = 7 \end{array}

Bab 3 Fungsi Kuadratik

Posted on May 16, 2016 by user

3.6 Fungsi Kuadratik, SPM Praktis (Soalan Pendek)

Soalan 1:

Cari nilai minimum bagi fungsi f (x) = 2x²+ 6x + 5. Nyatakan nilai xyang menjadikan f (x) satu nilai minimum.

Penyelesaian:

Menyempurnakan kuasa dua bagi f (x) dalam bentuk f (x) = a(x + p)² + q untuk mencari nilai minimum bagi fungsi f (x).

\begin{array}{l} f (x) = 2 x^{2} + 6 x + 5 \\ = 2 [x^{2} + 3 x + \frac{5}{2}] \\ = 2 [x^{2} + 3 x + {(3 \times \frac{1}{2})}^{2} - {(3 \times \frac{1}{2})}^{2} + \frac{5}{2}] \end{array}

\begin{array}{l} = 2 [{(x + \frac{3}{2})}^{2} - \frac{9}{4} + \frac{5}{2}] \\ = 2 [{(x + \frac{3}{2})}^{2} + \frac{1}{4}] \\ = 2 {(x + \frac{3}{2})}^{2} + \frac{1}{2} \end{array}

Didapati a = 2 > 0,

maka f (x) mempunyai nilai minimum apabila

x = - \frac{3}{2} .

Nilai minimum bagi f (x) = ½.

Soalan 2:

Fungsi kuadratik f (x) = –x²+ 4x + k², dengan keadaan k ialah pemalar, mempunyai nilai maksimum 8.

Cari nilai-nilai yang mungkin bagi k.

Penyelesaian:

f (x) = –x²+ 4x + k²

f (x) = –(x²– 4x) + k² ← [cara menyempurnakan kuasa dua bagi f (x)

dalam bentuk f (x) = a(x+ p)² + q]

f (x) = –[x²– 4x + (–2)² – (–2)²] + k²

f (x) = –[(x– 2)² – 4] + k²

f (x) = –(x– 2)² + 4 + k²

Diberi nilai maksimum ialah 8.

Maka, 4 + k²= 8

k² = 4

k = ±2

Bab 2 Persamaan Kuadratik

Posted on May 15, 2016 by user

2.5 Persamaan Kuadratik, SPM Praktis (Soalan Pendek)

Soalan 3:

Diberi bahawa 3 dan s + 4 ialah punca-punca bagi persamaan kuadratik

x ² + (t – 1)x + 6 = 0, dengan keadaan sdan t ialah pemalar.

Cari nilai s dan nilai t.

Penyelesaian:

x ² + (t – 1)x + 6 = 0

x ² – (1 – t)x+ 6 = 0

a = 1, b = (1 – t), dan c = 6

3 dan s + 4 ialah punca-punca bagi persamaan.

Guna Hasil darab punca untuk mencari nilai s.

3 \times (s + 4) = \frac{c}{a}

3 (s + 4) = 6

s + 4 = 2

s = –2

Guna Hasil tambah punca untuk mencari nilai t.

3 + (s + 4) = - \frac{b}{a}

3 + s + 4 = 1 – t

3 + (–2) + 4 – 1= – t

4 = – t

t = –4

Soalan 4:

Diberi satu daripada punca persamaan kuadratik x²– 9x + m = 0 ialah setengah kali punca yang satu lagi. Cari nilai bagi m.

Penyelesaian:

Katakan α dan β ialah dua punca bagi x² – 9x + m = 0.

Bandingkan x² – 9x + m = 0 dengan persamaan kuadratik ax² + bx + c = 0.

a = 1, b = –9, dan c = m.

Hasil tambah dua punca,

α + β = - \frac{b}{a} = - (\frac{- 9}{1}) = 9

\begin{array}{l} Katakan, \\ β = \frac{α}{2} \to \begin{array}{l} punca kedua ialah setengah \\ daripada punca pertama \end{array} \\ Dari α + β = 9 \\ α + \frac{α}{2} = 9 \\ \frac{3 α}{2} = 9 \\ α = 6 \end{array}

Hasil darab dua punca,

\begin{array}{l} α β = \frac{c}{a} \\ α (\frac{α}{2}) = m \\ m = \frac{α^{2}}{2} = \frac{6^{2}}{2} = 18 \end{array}

Bab 2 Persamaan Kuadratik

Posted on May 15, 2016 by user

2.5 Persamaan Kuadratik, SPM Praktis (Soalan Pendek)

Soalan 1:

Diberi persamaan kuadratik

mx ² + (3 – 2m)x+ m – 5 = 0.

Cari nilai m atau julat nilai m bagi setiap kes yang berikut.

(i) Jika persamaan kuadratik mempunyai dua punca yang nyata dan sama.

(ii) Jika persamaan kuadratik tidak mempunyai punca yang nyata.

Penyelesaian:

(i)

mx ² + (3 – 2m)x+ m – 5 = 0

a = m, b = 3 – 2m, dan c = m – 5

Bagi dua punca yang nyata dan sama,

b²– 4ac = 0

(3 – 2m)² – 4m (m – 5) = 0

9 – 12m + 4m²– 4m² + 20m = 0

8m= –9

m = - \frac{9}{8}

(ii)

Bagi dua punca nyata yang tidak wujud

b²– 4ac < 0

(3 – 2m)² – 4m (m – 5) < 0

9 – 12m + 4m²– 4m² + 20m < 0

8m + 9 < 0

m < - \frac{9}{8}

Soalan 2:

Cari nilai m jika garis lurus y = 5x – m ialah satu tangen kepada lengkung y = x²+ 2x + 1.

Penyelesaian:

Diberi

y = 5x – m -------- (1)

y = x² + 2x + 1 --- (2)

Gantikan (1) ke dalam (2)

5x – m = x² + 2x + 1

x ² – 3x + 1 + m = 0 ----- (3)

a = 1, b = –3, dan c = 1 + m

Tangen kepada lengkung mempunyai satu punca, iaitu

b²– 4ac = 0

(–3)²– 4(1) (1 + m) = 0

9 – 4 – 4m = 0

5 – 4m = 0

4m = 5

m = \frac{5}{4}

Bab 1 Fungsi

Posted on May 15, 2016 by user

1.5 Fungsi, SPM Praktis (Soalan Pendek)

Soalan 10:

Jika

g : x \to \frac{m - x}{x - 3}, x \neq 3

dan g ⁻ ¹ (5) = 14. Cari nilai m.

Penyelesaian:

Soalan 11 (Kaedah Bandingan):

Jika f : x \to \frac{m x - n}{x - 2}, x \neq 2 dan f^{- 1} : x \to \frac{5 - 2 x}{2 - x}, x \neq 2.

Cari nilai m dan n.

Penyelesaian:

\begin{array}{l} f (x) = \frac{m x - n}{x - 2} \\ Katakan y = \frac{m x - n}{x - 2} \to cari f^{- 1} (x) \\ y (x - 2) = m x - n \\ x y - 2 y = m x - n \\ x y - m x = 2 y - n \to \begin{array}{l} pindah x ke \\ sebelah kiri \end{array} \end{array}

\begin{array}{l} x (y - m) = 2 y - n \\ x = \frac{2 y - n}{y - m} \\ f^{- 1} (x) = \frac{2 x - n}{x - m} \\ \frac{2 x - n}{x - m} = \frac{5 - 2 x}{2 - x} \to \begin{array}{l} bandingkan dengan \\ f^{- 1} (x) yang diberi \end{array} \\ \times \frac{- 1}{- 1} \frac{n - 2 x}{m - x} = \frac{5 - 2 x}{2 - x} \\ maka, n = 5, m = 2 \end{array}

Soalan 12 (Kaedah Bandingan):

Diberi bahawa

f : x \to \frac{2 h}{x - 3 k}, x \neq 3 k,

dengan keadaan h dan k ialah pemalar dan

f^{- 1} : x \to \frac{14 + 24 x}{x}, x \neq 0.

Cari nilai h dan k .

Penyelesaian:

\begin{array}{l} f (x) = \frac{2 h}{x - 3 k} \\ Katakan y = \frac{2 h}{x - 3 k} \to cari f^{- 1} (x) \\ y (x - 3 k) = 2 h \\ x y - 3 k y = 2 h \\ x y = 2 h + 3 k y \\ x = \frac{2 h + 3 k y}{y} \end{array}

\begin{array}{l} f^{- 1} (x) = \frac{2 h + 3 k x}{x} \\ \frac{2 h + 3 k x}{x} = \frac{14 + 24 x}{x} \to \begin{array}{l} bandingkan dengan \\ f^{- 1} (x) yang diberi \end{array} \\ 2 h = 14 3 k = 24 \\ h = 7 k = 8 \end{array}

Bab 1 Fungsi

Posted on May 14, 2016 by user

1.5 Fungsi, SPM Praktis (Soalan Pendek)

Soalan 8:

Cari fungsi songsangan

f (x) = \frac{3 x + 2}{5 x + 3}

Penyelesaian:

\begin{array}{l} f (x) = \frac{3 x + 2}{5 x + 3} \\ katakan y = \frac{3 x + 2}{5 x + 3} \\ y (5 x + 3) = 3 x + 2 \\ 5 x y + 3 y = 3 x + 2 \\ 5 x y - 3 x = 2 - 3 y \\ x (5 y - 3) = 2 - 3 y \\ x = \frac{2 - 3 y}{5 y - 3} \\ f^{- 1} (x) = \frac{2 - 3 x}{5 x - 3} \to \begin{array}{l} tukar y kepada x \\ untuk cari f^{- 1} (x) \end{array} \end{array}

Soalan 9:

(a) Jika f : x → x – 2, cari f ^-1 (5),

(b) Jika f : x \to \frac{x + 9}{x - 5}, x \neq 5, cari f^{- 1} (3) .

Penyelesaian:

(a)

f (x) = x– 2

Katakan y = f ^-1(5)

f (y) = 5

y – 2 = 5

y = 7

oleh itu, f ^-1(5) = 7

(b)

\begin{array}{l} f (x) = \frac{x + 9}{x - 5} \\ katakan y = f^{- 1} (3) \\ f (y) = 3 \\ \frac{y + 9}{y - 5} = 3 \\ y + 9 = 3 y - 15 \\ 2 y = 24 \\ y = 12 \\ ∴ f^{- 1} (3) = 7 \end{array}

Bab 1 Fungsi

Posted on May 14, 2016 by user

1.5 Fungsi, SPM Praktis (Soalan Pendek)

Soalan 5:

Jika f : x → 2x + 1 dan

g : x \to \frac{5}{x}, x \neq 0

. Cari fungsi gubahan gf, fg dan nilai gf (4).

Penyelesaian:

Soalan 6:

Suatu fungsi f ditakrifkan oleh f : x → 2x + 1.
Cari fungsi gjika

f g : x \to \frac{5 x - 2}{x + 5}, x \neq - 5.

Penyelesaian:

[ Perhatian: Fungsi pertama diberi]

Soalan 7:

Suatu fungsi f ditakrifkan oleh

f : x \to \frac{7}{x} .

Cari fungsi g jika

g f : x \to \frac{10}{2 x + 3}, x \neq - \frac{3}{2} .

Penyelesaian:

[Perhatian: Fungsi kedua diberi, guna kaedah penggantian]