Bab 9 Pembezaan – user's Blog!

9.3 Kecerunan Tangen, Persamaan Tangen dan Persamaan Normal

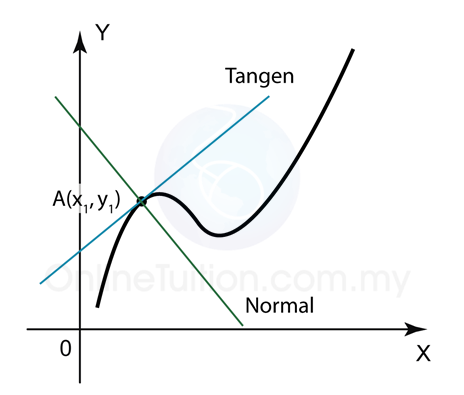
Jika A (x₁, y₁) adalah titik pada garis y = f (x), kecerunan garis (untuk garis lurus) atau kecerunan tangen garis (untuk suatu lengkung) adalah nilai

\frac{d y}{d x}

apabila x = x₁.

(A) Kecerunan tangent di A (x₁, y₁):

\frac{d y}{d x} = kecerunan tangen

(B) Persamaan tangen:

y – y₁ = m_tangen (x– x₁)

(C) Kecerunan normal di A (x₁, y₁):

\begin{array}{l} m_{normal} = - \frac{1}{m_{tangen}} \\ maka, \\ \frac{1}{- \frac{d y}{d x}} = kecerunan normal \end{array}

(D) Persamaan normal:

y – y₁ = m_normal (x– x₁)

Contoh 1 (Cari persamaan tangen)

Diberi bahawa

y = \frac{4}{{(3 x - 1)}^{2}}

. Cari persamaan tangen pada titik (1, 1).

Penyelesaian:

\begin{array}{l} y = \frac{4}{{(3 x - 1)}^{2}} = 4 {(3 x - 1)}^{- 2} \\ \frac{d y}{d x} = - 2.4 {(3 x - 1)}^{- 3} .3 \\ \frac{d y}{d x} = \frac{- 24}{{(3 x - 1)}^{3}} \\ Di titik (1, 1), \\ \frac{d y}{d x} = \frac{- 24}{{[3 (1) - 1]}^{3}} = \frac{- 24}{8} = - 3 \end{array}

Persamaan tangen di titik (1, 1) ialah,

y – 1 = – 3 (x – 1)

y – 1 = –3x + 3

y = –3x + 4

Contoh 2 (Cari persamaan normal)

Cari kecerunan lengkung

y = \frac{7}{3 x + 4}

di titik (–1, 7). Seterusnya, cari persamaan normal lengkung di titik itu.

Penyelesaian:

\begin{array}{l} y = \frac{7}{3 x + 4} = 7 {(3 x + 4)}^{- 1} \\ \frac{d y}{d x} = - 7 {(3 x + 4)}^{- 2} .3 \\ \frac{d y}{d x} = \frac{- 21}{{(3 x + 4)}^{2}} \\ Di titik (- 1, 7), \\ \frac{d y}{d x} = \frac{- 21}{{[3 (- 1) + 4]}^{2}} = - 21 \\ Persamaan normal = \frac{1}{21} \end{array}

Persamaan normal ialah,

y – y₁ = m (x – x₁)

y - 7 = \frac{1}{21} (x - (- 1))

21y – 147 = x + 1

21y – x – 148 = 0