Home › SPM Matematik Tambahan › Fungsi Trigonometri › Bab 16 Fungsi Trigonometri

Bab 16 Fungsi Trigonometri

Posted on by

5.5.1 Rumus bagi sin (A ± B), kos (A ± B), tan (A ± B), sin 2A, kos 2A, tan 2A
(Contoh Soalan)

Contoh 2:
Buktikan setiap identity trigonometri yang berikut.
(a) 1 + k o s 2 x sin 2 x = k o t x (b) k o t A sek 2 A = k o t A + tan 2 A (c) s i n x 1 − k o s x = k o t x 2

Penyelesaian:
(a)
Sebelah kiri = 1+kos2x sin2x = 1+( 2ko s 2 x−1 ) 2sinxkosx = 2 ko s 2 x 2 sinx kosx = kosx sinx =kotx=Sebelah kanan
 

(b)
Sebelah kanan =kotA+tan2A = kosA sinA + sin2A kos2A = kosAkos2A+sinAsin2A sinAkos2A = kosA( ko s 2 A− sin 2 A )+sinA( 2sinAkosA ) sinAkos2A
= ko s 3 A−kosA sin 2 A+2 sin 2 AkosA sinAkos2A = ko s 3 A+kosA sin 2 A sinAkos2A = kosA( ko s 2 A+ sin 2 A ) sinAkos2A = kosA sinAkos2A ← sin 2 A+ko s 2 A=1 =( kosA sinA )( 1 kos2A ) =kotAsek2A =Sebelah kiri


(c)
Sebelah kiri = sinx 1−kosx = 2sin x 2 kos x 2 1−( 1−2si n 2 x 2 ) ← sinx=2sin x 2 kos x 2 , kosx=1−2 sin 2 x 2 = 2 sin x 2 kos x 2 2 si n 2 x 2 = kos x 2 sin x 2 =kot x 2 =Sebelah kanan


Contoh 3:
(a) Diberi bahawa sinP= 3 5  dan sinQ= 5 13 ,  dengan keadaan P ialah satu sudut tirus dan Q ialah satu sudut cakah, tanpa menggunakan sifir atau kalkulator, cari nilai kos (P + Q).

(b) Diberi bahawa sinA=− 3 5  dan sinB= 12 13 ,  dengan keadaan A dan B adalah sudut-sudut dalam sukuan III dan sukuan IV masing-masing, tanpa menggunakan sifir atau kalkulator, cari nilai sin (A – B).

Penyelesaian:
(a)


 
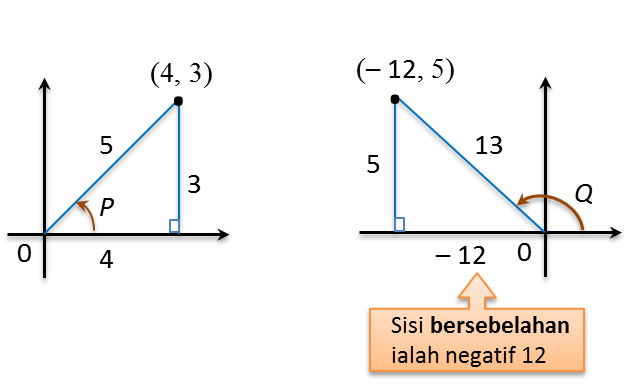
 sin P = 3 5 , k o s P = 4 5 sin Q = 5 13 , k o s Q = − 12 13 k o s ( P + Q ) = k o s A k o s B − sin A sin B = ( 4 5 ) ( − 12 13 ) − ( 3 5 ) ( 5 13 ) = − 48 65 − 15 65 = − 63 65
 

(b)



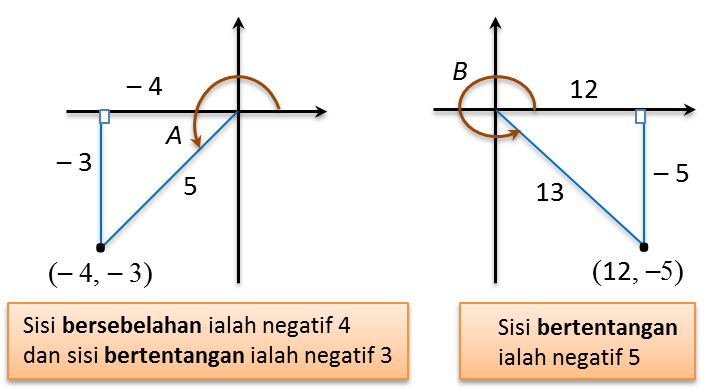
sin A = − 3 5 , k o s A = − 4 5 sin B = − 5 13 , k o s B = 12 13 s i n ( A − B ) = s i n A k o s B − k o s A sin B = ( − 3 5 ) ( 12 13 ) − ( − 4 5 ) ( − 5 13 ) = − 36 65 − 20 65 = − 56 65