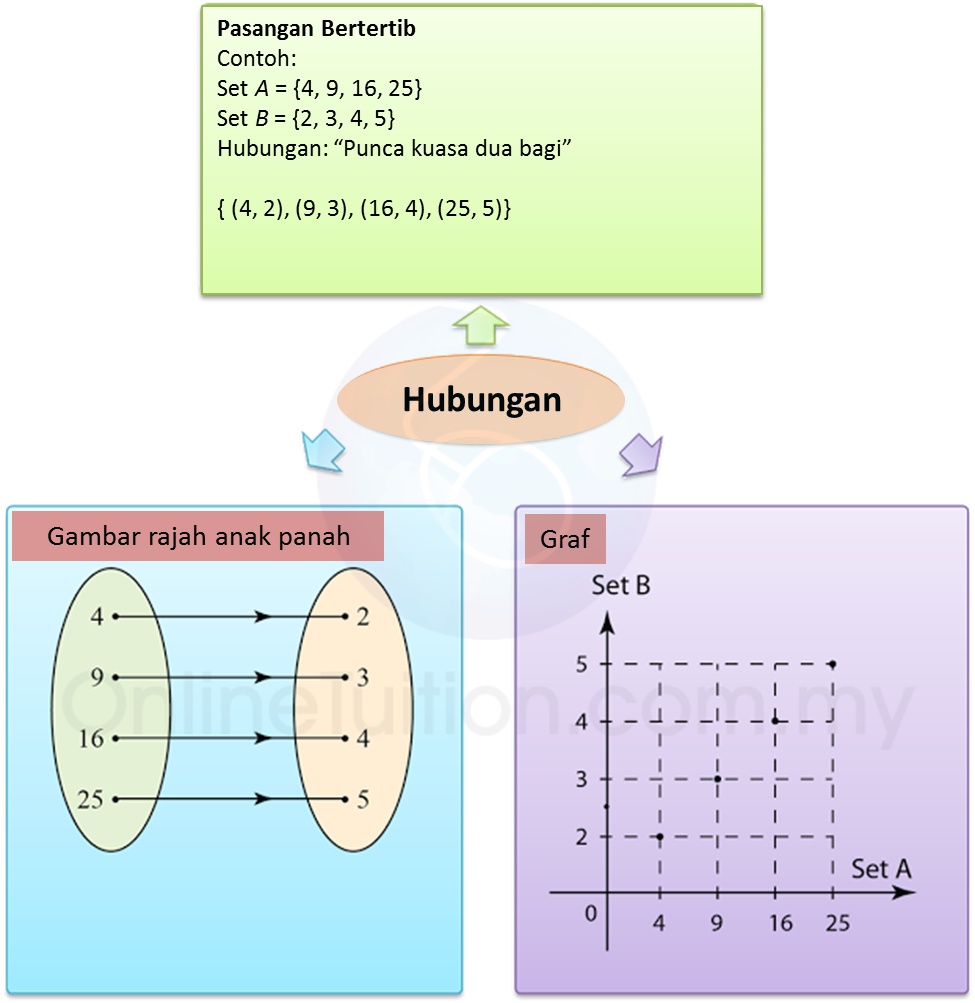
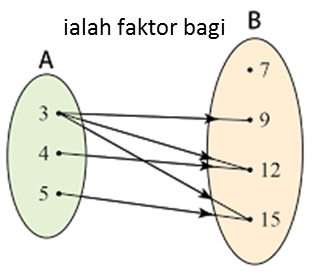
7.4 Statistik, SPM Praktis (Kertas 2)
Soalan 3:
Min bagi data 1, a, 2
a, 8, 9 dan 15 setelah disusun mengikut tertib menaik ialah b. Jika setiap nombor dalam data ditolak dengan 3, median baru ialah 47b.
Cari
(a) nilai a dan b,
(b) varians bagi data baru.
Penyelesaian:
(a)
Min ˉx=b1+a+2a+8+9+156=b
33 + 3a = 6b
3a = 6b – 33
a = 2b – 11 ---- (1)
Median baru =4b7(2a−3)+(8−3)2=4b72a+22=4b7
14a + 14 = 8b
7a = 4b – 7 ---- (2)
Gantikan (1) ke dalam (2),
7(2b – 11) = 4b – 7
14b – 77 = 4b – 7
10b = 70
b = 7
Dari (1),
a = 2(7) – 11 = 3
(b)
Data baru ialah (1 – 3), (3 – 3), (6 – 3), (8 – 3), (9 – 3), (15 – 3)
Maka data baru ialah – 2, 0, 3, 5, 6, 12
Varians, σ2=∑x2N−ˉx2σ2=(−2)2+(0)2+(3)2+(5)2+(6)2+(12)26 −(−2+0+3+5+6+126)2σ2=2186−16=20.333
Soalan 4:
Satu set data mengandungi 20 nombor. Min bagi nombor itu ialah 8 dan sisihan piawai ialah 3.
(a) Hitungkan ∑x dan ∑x2.
(b) Hasil tambah nombor tertentu ialah 72 dengan min ialah 9 dan hasil tambah kuasa dua nombor-nombor itu ialah 800, dikeluarkan dari set 20 nombor itu. Hitung min dan sisihan piawai baki nombor.
Penyelesaian:
(a)
Min ˉx=∑xN8=∑x20∑x=160
Sisihan piawai, σ=√∑x2N−ˉx23=√∑x2N−ˉx29=∑x220−82∑x220=73∑x2=1460
(b)
Hasil tambah nombor tertentu, M ialah 72 dengan min 9,
72M=9M=8
Min baki nombor
=160−7220−8=713
Varians baki nombor
=1460−80012−(713)2=55−5379=129