4.7 Vektor, SPM Praktis (Kertas 2)
Soalan 1:
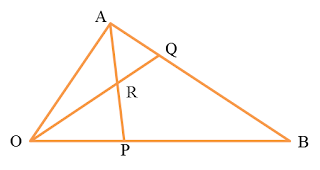
Rajah di atas menunjukkan segi tiga OAB. Garis lurus AP bersilang dengan garis lurus OQpada titik R.
Diberi bahawa OP=14OB, AQ=14AB, →OP=4b˜ dan →OA=8a˜.
(a)
Ungkapakan dalam sebutan a˜ dan b˜:
(i) →AP
(ii) →OQ
(b)
(i) Diberi bahawa →AR=h→AP, nyatakan →AR dalam sebutan h, a˜ dan b˜.
(ii) Diberi bahawa →RQ=k→OQ, nyatakan →AR dalam sebutan k, a˜ dan b˜.
(c)
Dengan menggunakan →AQ=→AR+→RQ ,
cari nilai bagi h dan k.
Penyelesaian:
(a)(i)
→AP=→AO+→OP→AP=−→OA+→OP→AP=−8a˜+4b˜
(a)(ii)
→OQ=→OA+→AQ→OQ=8a˜+14→AB→OQ=8a˜+14(→AO+→OB)→OQ=8a˜+14(−8a˜+4→OP)→OQ=8a˜+14(−8a˜+4(4b˜))→OQ=8a˜−2a˜+4b˜→OQ=6a˜+4b˜
(b)(i)
→AR=h→AP→AR=h(−8a˜+4b˜)→AR=−8ha˜+4hb˜
(b)(ii)
→RQ=k→OQ→RQ=k(6a˜+4b˜)→RQ=6ka˜+4kb˜
(c)
→AQ=→AR+→RQ→AQ=−8ha˜+4hb˜+(6ka˜+4kb˜)→AO+→OQ=−8ha˜+4hb˜+6ka˜+4kb˜−8a˜+6a˜+4b˜=−8ha˜+4hb˜+6ka˜+4kb˜−2a˜+4b˜=−8ha˜+4hb˜+6ka˜+4kb˜
–2 = –8h + 6k
–1 = –4h + 3k → (1)
4 = 4h + 4k
1 = h + k
k= 1 – h → (2)
Gantikan (2) ke dalam (1),
–1 = –4h + 3 (1 – h)
–1 = –4h + 3 – 3h
–4 = –7h
h=47Daripada (2),k=1−47=37