Home › 2016 › July › Page 4

Monthly Archives: July 2016

Bab 3 Fungsi Kuadratik

Posted on by
3.5a Jenis Punca Persamaan Kuadratik (Contoh Soalan)

Contoh 1 (Garis Lurus adalah Tangen kepada Lengkung)
Cari nilai p jika 8y= x + 2p adalah tangen kepada lengkung 2y2 = x+ p.


Penyelesaian:




Bab 3 Fungsi Kuadratik

Posted on by
3.5 Jenis Punca Persamaan Kuadratik
1.      Jenis punca persamaan kuadratik ax2  + bx + c= 0 ditentukan oleh nilai b2 − 4ac. Nilai b2 − 4ac memberi maklumat terhadap bilangan titik persilangan.

(a)  Apabila graf menyentuh garis lurus pada satu titik, iaitu terdapat hanya satu punca nyata bagi persamaan ax2  + bx + c = 0, maka b2  − 4ac = 0.




(b)  Apabila graf bersilang dengan garis lurus pada dua titik, iaitu terdapat dua punca nyata dan berbeza bagi persamaan ax2  + bx + c = 0, maka b2  − 4ac > 0.





(c)  Apabila graf tidak bersilang dengan garis lurus (tiada titik persilangan), iaitu tidak terdapat punca nyata bagi persamaan ax2  + bx + c = 0, maka b2  − 4ac < 0.



Bab 3 Fungsi Kuadratik

Posted on by
3.4 Ketaksamaan Kuadratik (Bahagian 2)

(C) Ketaksamaan Linear
Contoh 1:
(a) Diberi x= 6−y 3 , cari julat nilai x untuk y > 9.
(b) Diberi 2x + 3y – 6 = 0, cari julat nilai x untuk y < 4.

Penyelesaian:






(D) Ketaksamaan Kuadratik
Contoh 2:
Cari julat nilai x yang memuaskan setiap ketaksamaan kuadratik yang berikut:
(a) (2x+ 1) (3x – 1) < 14
(b) (x – 2) (5x – 4) + 1 > 0

Penyelesaian:





Bab 2 Persamaan Kuadratik

Posted on by
2.2b Penyempurnaan Kuasa Dua (Contoh Soalan)

(A) Langkah-langkah untuk menyelesaikan persamaan kuadratik dengan menggunakan cara penyempurnaan kuasa dua.

• pastikan pekali bagi x ialah 1.
• Tulis semula persamaan ax 2 + bx + c = 0 dalam bentuk ax 2 + bx = –c  
• Tambah  ( pekali bagi x 2 ) 2  pada kedua-dua belah persamaan.


Contoh:
Selesaikan setiap persamaan kuadratik berikut dengan cara penyempurnaan kuasa dua.
(a) 2x 2 – 5x – 7 = 0
(b) x 2 +1= 10 3 x

Penyelesaian:






Bab 2 Persamaan Kuadratik

Posted on by
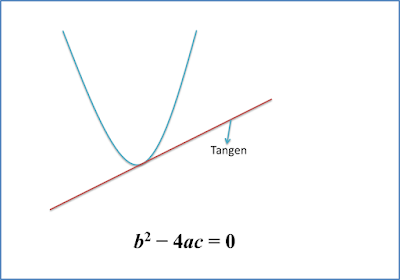
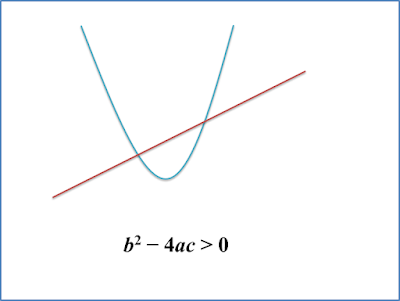
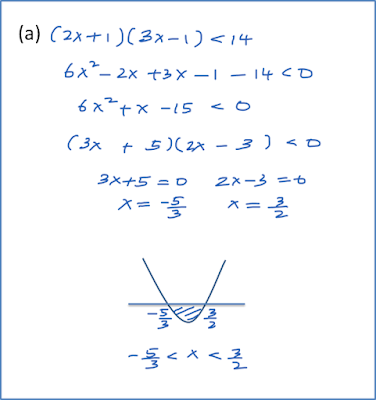2.2b Penyempurnaan Kuasa Dua

(A) Penyempurnaan Kuasa Dua
1.      Ungkapan x 2 + 2x + 1 boleh ditulis dalam bentuk (x + 1)2 yang dikenali sebagai ‘kuasa dua sempurna’. Sebagai contoh x 2 + 2x + 1 = (x + 1)2 .

Contoh:
Selesaikan setiap persamaan kuadratik yang berikut
(a) (x + 1)2 = 25
(b) x2 − 8x + 16 = 49

Penyelesaian:
(a)
(x + 1)2 = 25
(x + 1)2 = ±√25
x = −1 ± 5
x = 5  atau  x = −6

(b)
x 2 − 8x + 16 = 49
(x − 4)2 = 49
(x − 4) = ±√49
x = 4 ± 7
x = 11  atau  x = −3


(B) Selesaikan Persamaan Kuadratik dengan Cara Penyempurnaan Kuasa Dua

1. Untuk menyelesaikan persamaan kuadratik, kita membuat persamaan di sebelah kiri sebagai suatu kuasa dua sempurna.
2. Untuk membentuk sebarang ungkapan kuadratik x2 + px kepada suatu kuasa dua sempurna, kita menambahkan ( p 2 ) 2   ke dalam ungkapan itu untuk menjadikan x 2 +px= x 2 +px+ ( p 2 ) 2 = ( x+ p 2 ) 2
3. Langkah-langkah berikut diambil untuk menyelesaikan persamaan kuadratik ax2 + bx = – c dengan menggunakan cara penyempurnaan kuasa dua.
 (a) Tulis semula persamaan ax 2 + bx + c = 0 dalam bentuk ax2 + bx = – c.
 (b) Jika pekali a ≠ 1, tukarkannya kepada 1 (dengan pembahagian).
 (c) Tambah ( p 2 ) 2   iaitu ( pekali bagi x 2 ) 2   pada kedua-dua belah persamaan.
 (d) Tulis ungkapan pada sebelah kiri sebagai kuasa dua sempurna.
 (e) Selesaikan persamaan itu .


Contoh:
Selesaikan persamaan kuadratik x 2 – 6x – 3 = 0 dengan cara penyempurnaan kuasa dua.

Penyelesaian:
x 2 – 6x – 3 = 0 ← (pekali bagi x 2 = 1)
x 2 – 6x = 3 ← (pekali bagi x = b = –6)
x 2 – 6x + [½ × (–6)]2 = 3 + [½ × (–6)]2 ← [tambah ( pekali bagi x 2 ) 2   iaitu (½ × (–6)2, pada kedua-dua belah persamaan]
x 2 – 6x + (–3)2 = 3 + (–3)2
(x – 3)2 = 12
x – 3 = ±√12
x = 3 ± √12
x = 3 + √12   atau   3 – √12 
x = 6.464      atau   –0.464