Soalan 3:
Rajah di bawah menunjukkan sebuah segi tiga ABC.
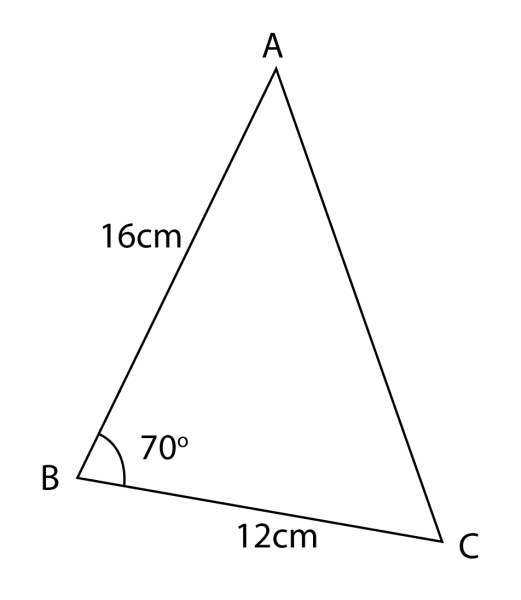

(a) Hitungkan panjang, dalam cm, bagi AC.
(b) Suatu sisi empat ABCD dibentuk dengan keadaan AC ialah pepenjuru, ∠ACD = 45° dan AD = 14 cm.
Hitung dua nilai yang mungkin bagi ∠ADC.
(c) Dengan menggunakan ∠ADC yang tirus dari (b), hitungkan
i. panjang, dalam cm, bagi CD,
ii. luas, dalam cm2, sisi empat ABCD itu
i. panjang, dalam cm, bagi CD,
ii. luas, dalam cm2, sisi empat ABCD itu
Penyelesaian:
(a)
Guna petua kosinus,
AC2 = AB2 + BC2 – 2 (AB)(BC) kos ∠ABC
AC2 = 162 + 122 – 2 (16)(12) kos 70o
AC2 = 400 – 131.33
AC2 = 268.67
AC = 16.39 cm
(b)
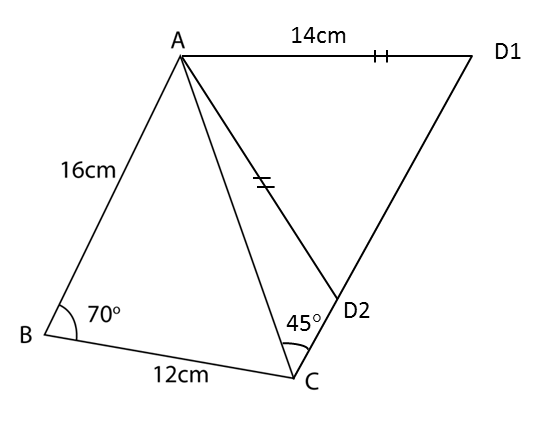
Guna petua sinus,sin∠ADC16.39=sin45∘14sin∠ADC=16.39×sin45∘14
sin ∠ ADC = 0.8278
∠ ADC = 55.87o atau (180o – 55.87o)
∠ ADC = 55.87o atau 124.13o
(c)(i)
sudut tirus ADC = 55.87o
∠ CAD = 180o – 45o – 55.87o = 79.13o
CDsin79.13∘=14sin45∘CD=14×sin79.13∘sin45∘=19.44cm
(c)(ii)
Luas sisi empat ABCD
= Luas ∆ ABC + Luas ∆ ACD
= ½ (16)(12) sin 70o+ ½ (16.39)(14) sin79.13o
= 90.21 + 112.67
= 202.88 cm2