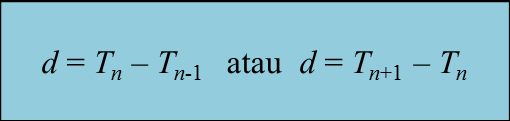Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 3:

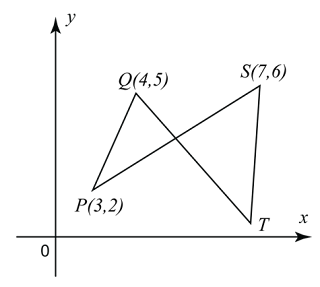
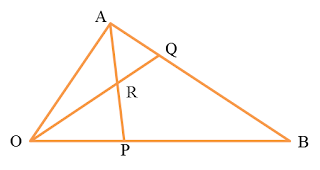
Dalam rajah di atas, PRS dan QRT ialah garis lurus. Diberi Radalah titik tengah bagi PS dan QR : RT = 1 : 3, Cari

(a) koordinat titik R,

(b) koordinat titik T,

(c) koordinat bagi titik persilangan antara garis PQ dan garis ST.

Penyelesaian:

(a)

Diberi R ialah titik tengah bagi PS.

\begin{array}{l} R = (\frac{3 + 7}{2}, \frac{2 + 6}{2}) \\ R = (5, 4) \end{array}

(b)

QR : RT = 1 : 3

Katakan koordinat titik T = (x, y)

\begin{array}{l} (\frac{(1) (x) + (3) (4)}{1 + 3}, \frac{(1) (y) + (3) (5)}{1 + 3}) = (5, 4) \\ \frac{x + 12}{4} = 5 \\ x + 12 = 20 \\ x = 8 \\ \frac{y + 15}{4} = 4 \end{array}

y + 15 = 16

y = 1

T = (8, 1)

(c)

Kecerunan P Q = \frac{5 - 2}{4 - 3} = 3

Persamaan PQ,

y – 2 = 3 (x – 3)

y – 2 = 3x – 9

y = 3x – 7 ---- (1)

Kecerunan S T = \frac{6 - 1}{7 - 8} = - 5

Persamaan ST,

y – 1 = –5 (x – 8)

y – 1 = –5x + 40

y = –5x + 41 ---- (2)

Gantikan (1) ke dalam (2),

3x – 7 = –5x + 41

8x = 48

x = 6

Dari (1),

y = 3(6) – 7 = 11

Koordinat bagi titik persilangan antara garis PQ dan garis ST = (6, 11).

Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.7 Geometri Koordinat, SPM Praktis (Kertas 1)

Soalan 6:

Titik M ialah (-3, 5) dan titik N ialah (4, 7). Titik P bergerak dengan keadaan PM: PN= 2: 3. Cari persamaan lokus bagi P.

Penyelesaian:

Katakan P = (x, y)

PM : PN = 2 : 3

\begin{array}{l} \frac{P M}{P N} = \frac{2}{3} \\ 3 P M = 2 P N \\ 3 \sqrt{{(x - (- 3))}^{2} + {(y - 5)}^{2}} = 2 \sqrt{{(x - 4)}^{2} + {(y - 7)}^{2}} \end{array}

Menguasa dua kedua-dua belah untuk menghapuskan punca kuasa dua.

9[x²+ 6x + 9 + y² – 10y + 25] = 4 [x² – 8x + 16 + y² – 14y + 49]

9x²+ 54x + 9y² – 90y + 306 = 4x² – 32x + 4y²– 56y + 260

5x²+ 5y² + 86x – 34y + 46 = 0

Oleh itu, persamaan lokus bagi titik P ialah

5x² + 5y² + 86x – 34y + 46 = 0

Soalan 7:

Diberi titik A (0,2) dan titik B (6,5). Cari persamaan lokus bagi suatu titik bergerak P dengan keadaan APB sentiasa bersudut tegak di P.

Penyelesaian:

Katakan P = (x, y)

Diberi segi tiga APB = 90^o, maka AP adalah berserenjang dengan PB.

Oleh itu, (m_AP)(m_PB) = –1.

(m_AP)(m_PB) = –1

(\frac{y - 2}{x - 0}) (\frac{y - 5}{x - 6}) = - 1

(y – 2)(y – 5) = – x(x – 6)

y² – 7y + 10 = –x² + 6x

y² + x² – 6x – 7y + 10 = 0

Persamaan lokus bagi titik P ialah,

y² + x² – 6x – 7y + 10 = 0

Soalan 8:

Cari persamaan pembahagi dua sama serenjang bagi garis lurus yang menyambungkan titik (–4, 3) dengan titik (2, 4).

Penyelesaian:

Kecerunan garis, m₁=

\frac{4 - 3}{2 - (- 4)} = \frac{1}{6}

Kecerunan garis serenjang, m₂ =

- \frac{1}{m_{1}} = - 6

\begin{array}{l} Titik tengah = (\frac{- 4 + 2}{2}, \frac{3 + 4}{2}) \\ = (- 1, \frac{7}{2}) \end{array}

Jadi, persamaan pembahagi dua sama serenjang ialah

\begin{array}{l} y - \frac{7}{2} = - 6 (x - (- 1)) \\ y - \frac{7}{2} = - 6 x - 6 \end{array}

2y – 7 = –12x – 12

12x + 2y + 5 = 0

Bab 15 Vektor

Posted on July 7, 2016 by user

4.7 Vektor, SPM Praktis (Kertas 2)

Soalan 3:

Dalam rajah di bawah, PQRS ialah satu segi empat. PTSdan TUR ialah garis lurus.

Diberi bahawa

\vec{P Q} = 20 \underset{˜}{x}, \vec{P T} = 8 \underset{˜}{y}, \vec{S R} = 25 \underset{˜}{x} - 24 \underset{˜}{y}, \vec{P T} = \frac{1}{4} \vec{P S} dan \vec{T U} = \frac{3}{5} \vec{T R}

(a) Ungkapakan dalam sebutan

\underset{˜}{x} dan/ atau \underset{˜}{y} :

(i)

\vec{Q S}

(ii)

\vec{T R}

(b) Tunjukkan titik Q, Udan S adalah segaris.

| \underset{˜}{x} | = 2 dan | \underset{˜}{y} | = 3, cari | \vec{Q S} |

Penyelesaian:

(a)

\begin{array}{l} \vec{Q S} = \vec{Q P} + \vec{P S} \\ \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \leftarrow \begin{array}{l} Diberi \vec{P T} = \frac{1}{4} \vec{P S} \\ \vec{P S} = 4 \vec{P T} = 4 (8 \underset{˜}{y}) = 32 \underset{˜}{y} \end{array} \end{array}

(b)

\begin{array}{l} \vec{T R} = \vec{T S} + \vec{S R} \\ \vec{T R} = \frac{3}{4} \vec{P S} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = \frac{3}{4} (32 \underset{˜}{y}) + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 24 \underset{˜}{y} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 25 \underset{˜}{x} \end{array}

(c)

\begin{array}{l} \vec{Q U} = \vec{Q P} + \vec{P T} + \vec{T U} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + \frac{3}{5} (25 \underset{˜}{x}) \leftarrow \begin{array}{l} Diberi \\ \vec{T U} = \frac{3}{5} \vec{T R} \end{array} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + 15 \underset{˜}{x} \\ \vec{Q U} = - 5 \underset{˜}{x} + 8 \underset{˜}{y} \end{array}

\begin{array}{l} Dari (a)(i) \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{- 20 \underset{˜}{x} + 32 \underset{˜}{y}}{- 5 \underset{˜}{x} + 8 \underset{˜}{y}} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{4 (- 5 \underset{˜}{x} + 8 \underset{˜}{y})}{(- 5 \underset{˜}{x} + 8 \underset{˜}{y})} \\ \frac{\vec{Q S}}{\vec{Q U}} = 4 \\ \vec{Q S} = 4 \vec{Q U} \end{array}

Oleh itu, Q, U dan S adalah segaris.

(d)

\begin{array}{l} \vec{P S} = 32 \underset{˜}{y} \\ | \vec{P S} | = 32 | \underset{˜}{y} | \\ | \vec{P S} | = 32 \times 3 = 96 \\ \vec{P Q} = 20 \underset{˜}{x} \\ | \vec{P Q} | = 20 | \underset{˜}{x} | \\ | \vec{P Q} | = 20 \times 2 = 40 \\ Oleh itu | \vec{Q S} | = \sqrt{96^{2} + 40^{2}} \\ | \vec{Q S} | = 104 \end{array}

Bab 15 Vektor

Posted on July 6, 2016 by user

4.7 Vektor, SPM Praktis (Kertas 2)

Soalan 1:

Rajah di atas menunjukkan segi tiga OAB. Garis lurus AP bersilang dengan garis lurus OQpada titik R.

Diberi bahawa

O P = \frac{1}{4} O B, A Q = \frac{1}{4} A B, \vec{O P} = 4 \underset{˜}{b} dan \vec{O A} = 8 \underset{˜}{a} .

(a) Ungkapakan dalam sebutan

\underset{˜}{a} dan \underset{˜}{b} :

(i)

\vec{A P}

(ii)

\vec{O Q}

(b) (i) Diberi bahawa

\vec{A R} = h \vec{A P}, nyatakan \vec{A R} dalam sebutan h, \underset{˜}{a} dan \underset{˜}{b} .

(ii) Diberi bahawa

\vec{R Q} = k \vec{O Q}, nyatakan \vec{A R} dalam sebutan k, \underset{˜}{a} dan \underset{˜}{b} .

\vec{A Q} = \vec{A R} + \vec{R Q},

cari nilai bagi h dan k.

Penyelesaian:

(a)(i)

\begin{array}{l} \vec{A P} = \vec{A O} + \vec{O P} \\ \vec{A P} = - \vec{O A} + \vec{O P} \\ \vec{A P} = - 8 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}

(a)(ii)

\begin{array}{l} \vec{O Q} = \vec{O A} + \vec{A Q} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} \vec{A B} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (\vec{A O} + \vec{O B}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 \vec{O P}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 (4 \underset{˜}{b})) \\ \vec{O Q} = 8 \underset{˜}{a} - 2 \underset{˜}{a} + 4 \underset{˜}{b} \\ \vec{O Q} = 6 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}

(b)(i)

\begin{array}{l} \vec{A R} = h \vec{A P} \\ \vec{A R} = h (- 8 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{A R} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} \end{array}

(b)(ii)

\begin{array}{l} \vec{R Q} = k \vec{O Q} \\ \vec{R Q} = k (6 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{R Q} = 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}

(c)

\begin{array}{l} \vec{A Q} = \vec{A R} + \vec{R Q} \\ \vec{A Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + (6 k \underset{˜}{a} + 4 k \underset{˜}{b}) \\ \vec{A O} + \vec{O Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 8 \underset{˜}{a} + 6 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 2 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}

–2 = –8h + 6k

–1 = –4h + 3k → (1)

4 = 4h + 4k

1 = h + k

k= 1 – h → (2)

Gantikan (2) ke dalam (1),

–1 = –4h + 3 (1 – h)

–1 = –4h + 3 – 3h

–4 = –7h

\begin{array}{l} h = \frac{4}{7} \\ Daripada (2), \\ k = 1 - \frac{4}{7} = \frac{3}{7} \end{array}

Bab 5 Indeks dan Logaritma

Posted on July 6, 2016 by user

5.3 Persamaan yang Melibatkan Indeks (Contoh Soalan)

Contoh 5 [Asas tidak sama – tukar kepada bentuk lagaritma biasa (log₁₀) bagi kedua-dua belah]:

Selesaikan setiap persamaan yang berikut.

(a) 3^x ⁺ ¹ = 7
(b) 2 (3^x ) = 5
(c) 2^x .3^x = 9^x ⁻ ⁴
(d) 5^x ⁻ ¹.3^x ⁺ ² = 10

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on July 6, 2016 by user

5.2 Logaritma

N = a^x ↔ log_aN = x

log_a N = x ialah bentuk logaritma manakala N = a^x ialah bentuk index.

Takrif Logaritma:

1. Jika aialah nombor positif, maka a^xjuga nombor positif. Logaritma bagi nombor negatif adalah tidak tertakrif.

2. Logaritma yang asasnya 10 dikenali sebagai logaritma biasa. Simbolnya ialah log₁₀, singkatannya lg.

3. Nilai logaritma biasa dapat dicari dengan menggunakan kalkulator saintifik.

4. Bagi asas logaritma bukan 10, asanya perlu dinyatakan, misalnya log₃81.

5. Logaritma boleh berasas sebarang nombor positif, kecuali 1,

(a) log_a1 = 0

(b) log_aa= 1

Contoh 1:

Cari persamaan-persamaan berikut:

(a) log₂ 64

(b) log₃ 1

(d) log_½ 4

(e) log₈ 0.25

Penyelesaian:

Contoh 2:

Cari persamaan-persamaan berikut:

(a) log₃ 5x = 2

(b) log_x_{+ 1} 81 = 2

Penyelesaian:

Bab 15 Vektor

Posted on July 5, 2016 by user

4.5 Vektor dalam Satah Cartes

1. Vektor unit mempunyai magnitud satu unit.

2. Vektor

\underset{˜}{i}

ialah vektor unit ke arah positif paksi-x.

Vektor

\underset{˜}{j}

ialah vektor unit ke arah positif paksi-y.

3. Suatu vektor dalam satah Cartes boleh ditulis dalam bentuk

x \underset{˜}{i} + y \underset{˜}{j} atau vektor lajur (\begin{array}{l} x \\ y \end{array}) .

4. Magnitud bagi vektor unit ialah

| \underset{˜}{i} | = | \underset{˜}{j} | = 1.

5. Magnitud bagi vektor

\vec{O A} = x \underset{˜}{i} + y \underset{˜}{j} diberi oleh | \vec{O A} | = \sqrt{x^{2} + y^{2}} .

Contoh 1:

Jika

\underset{˜}{r} = k \underset{˜}{i} - 8 \underset{˜}{j} dan | \underset{˜}{r} | = 10,

cari nilai k. Tentukan vektor unit dalam arah

\underset{˜}{r}

bagi setiap nilai k.

Penyelesaian:

\begin{array}{l} Diberi | \underset{˜}{r} | = 10 \\ \sqrt{x^{2} + y^{2}} = 10 \\ \sqrt{k^{2} + {(- 8)}^{2}} = 10 \\ k^{2} + 64 = 100 \\ k = \pm 6 \end{array}

\begin{array}{l} Vektor unit, \hat{\underset{˜}{r}} = \frac{x \underset{˜}{i} + y \underset{˜}{j}}{\sqrt{x^{2} + y^{2}}} \\ Apabila k = 6, Apabila k = - 6 \\ \hat{\underset{˜}{r}} = \frac{6 \underset{˜}{i} - 8 \underset{˜}{j}}{10} = \frac{3 \underset{˜}{i} - 4 \underset{˜}{j}}{5} \hat{\underset{˜}{r}} = \frac{- 6 \underset{˜}{i} - 8 \underset{˜}{j}}{10} = \frac{- 3 \underset{˜}{i} - 4 \underset{˜}{j}}{5} \\ \hat{\underset{˜}{r}} = \frac{1}{5} (3 \underset{˜}{i} - 4 \underset{˜}{j}) \hat{\underset{˜}{r}} = \frac{1}{5} (- 3 \underset{˜}{i} - 4 \underset{˜}{j}) \end{array}

Contoh 2:

Diberi bahawa

\underset{˜}{a} = (\begin{array}{l} 6 \\ 3 \end{array}) dan \underset{˜}{b} = (\begin{array}{l} 3 \\ 7 \end{array}) .

(a) Cari

\underset{˜}{b} - \underset{˜}{a} dan | \underset{˜}{b} - \underset{˜}{a} | .

(b) Seterusnya, cari vektor unit dalam arah

\underset{˜}{b} - \underset{˜}{a} .

Penyelesaian:

(a)

\begin{array}{l} \underset{˜}{b} - \underset{˜}{a} = (\begin{array}{l} 3 \\ 7 \end{array}) - (\begin{array}{l} 6 \\ 3 \end{array}) \\ = (\begin{array}{l} 3 - 6 \\ 7 - 3 \end{array}) \\ = (\begin{array}{l} - 3 \\ 4 \end{array}) \\ | \underset{˜}{b} - \underset{˜}{a} | = \sqrt{{(- 3)}^{2} + 4^{2}} \\ = \sqrt{9 + 16} \\ = \sqrt{25} = 5 \end{array}

(b)

\begin{array}{l} Vektor unit dalam arah \underset{˜}{b} - \underset{˜}{a} \\ = \frac{1}{5} (\begin{array}{l} - 3 \\ 4 \end{array}) \\ = (\begin{array}{l} - \frac{3}{5} \\ \frac{4}{5} \end{array}) \end{array}

Bab 15 Vektor

Posted on July 5, 2016 by user

4.1 Pengenalan Vektor

(A) Kuantiti Vektor dan Kuantiti Skalar

1. Vektor ialah kuantiti yang mempunyai maginitud dan arah.

2. Skalar ialah kuantiti yang mempunyai magnitud sahaja.

3. Misalnya, magnitud vektor

\vec{O A}

ialah panjang OA dan arahnya adalah dari O ke A.

\vec{O A}

boleh ditandakan sebagai

\underset{˜}{a}

dan magnitudnya pula ditandakan sebagai

| \vec{O A} | atau | \underset{˜}{a} | .

(B) Vektor sebagai Garis Terarah

1. Vektor

\vec{A B}

mewakili satu vektor yang mempunyai magnitud

\vec{A B}

dan menghala dari A ke B. Magnitud

\vec{A B}

ditulis sebagai

| \vec{A B} |

(C) Kesamaan Dua Vektor

1. Dua vektor adalah sama jika kedua-duanya mempunyai magnitud dan arah yang sama.
Misalnya,

\begin{array}{l} \underset{˜}{a} = \underset{˜}{b} \\ Jika (a) | \underset{˜}{a} | = | \underset{˜}{b} |, \\ (b) arah \underset{˜}{a} dan \underset{˜}{b} sama . \end{array}

2. Vektor negatif bagi

\vec{A B}

ialah vektor yang mempunyai magnitud yang sama dengan

\vec{A B}

tetapi dalam arah yang bertentangan dengan arah

\vec{A B}

. Vektor negatif bagi

\vec{A B}

boleh
ditulis sebagai

- \vec{A B} atau \vec{B A}

. Vektor negatif bagi

\underset{˜}{a} ditulis sebagai - \underset{˜}{a} .

3. Vektor sifar,

\underset{˜}{0}

, ialah vektor yang mempunyai magnitud sifar dan arahnya tidak tertakrif.

Bab 12 Janjang

Posted on July 5, 2016 by user

1.2.1 Janjang Geometri

(A) Ciri-ciri Janjang Geometri

Janjang Geometri (J.G.) ialah satu jujukan nombor yang setiap sebutan (kecuali sebutan pertama) diperoleh dengan mendarabkan satu pemalar kepada sebutan sebelumnya. Pemalar ini dikenal sebagai nisbah sepunya, r.

Contoh:

Tentukan sama ada jujukan nombor yang berikut ialah janjang geometri (J.G.) atau bukan janjang geometri.

(a) 1, 4, 16, 64, …..

(b) 10, –5, 2.5, –1.25, …..

(c) 2, 4, 12, 48, …..

[Tip pintar: Bagi suatu janjang geometri, sentiasa darab satu nombor tetap untuk mendapat nombor seterusnya]

Penyelesaian:

(a)

\begin{array}{l}  \end{array}

\begin{array}{l} Nisbah sepunya, r = \frac{T_{n}}{T_{n - 1}} \\ \frac{T_{3}}{T_{2}} = \frac{16}{4} = 4, \frac{T_{2}}{T_{1}} = \frac{4}{1} = 4 \\ \frac{T_{3}}{T_{2}} = \frac{T_{2}}{T_{1}} \end{array}

1, 4, 16, 64, …. ialah JG, a = 1, r = 4.

(b)

\begin{array}{l} Nisbah sepunya, \\ r = \frac{T_{2}}{T_{1}} = - \frac{5}{10} = - \frac{1}{2} \end{array}

10, –5, 2.5, –1.25, ….., ialah JG, a = 1, r = – ½.

(c)

\begin{array}{l} Nisbah sepunya, \\ r = \frac{T_{2}}{T_{1}} = \frac{4}{2} = 2 \\ r = \frac{T_{3}}{T_{2}} = \frac{12}{4} = 3 \\ \frac{T_{2}}{T_{1}} \neq \frac{T_{3}}{T_{2}} \end{array}

2, 4, 12, 48, …..Bukan JG.

kerana nisbah antara nombor-nombor yang berturutan tidak sama.

(B) Langkah-langkah untuk membuktikan sama ada jujukan nombor yang diberi ialah satu janjang geometri.

Langkah 1: Senaraikan tiga sebutan yang berturutan. [Contoh: T₁, T₂, T₃.]

Langkah 2: Hitung nilai bagi

\frac{T_{3}}{T_{2}} dan \frac{T_{2}}{T_{1}} .

Langkah 3: Jika

\frac{T_{3}}{T_{2}} = \frac{T_{2}}{T_{1}} = r

, maka jujukan nombor itu ialah satu janjang geometri.

Langkah 4: Jika

\frac{T_{3}}{T_{2}} \neq \frac{T_{2}}{T_{1}}

, maka jujukan nombor itu bukan satu janjang geometri.

Bab 12 Janjang

Posted on July 5, 2016 by user

1.1 Janjang Aritmetik

(A) Ciri-ciri Janjang Aritmetik

1. Jujukan ialah suatu set nombor yang mengikut suatu pola tertentu.Misalnya: 4, 7, 10, 13, … ialah satu jujukan.

2. Setiap nombor dalam suatu jujukan dikenali sebagai sebutan.

3. Janjang aritmetik (J.A.) ialah satu jujukan nombor yang setiap sebutan (kecuali sebutan pertama) diperoleh dengan menambahkan satu pemalar kepada sebutan sebelumnya. Pemalar ini dikenal sebagai beza sepunya, d.

Contoh:

Tentukan sama ada jujukan nombor yang berikut ialan janjang aritmetik (J.A.) atau bukan janjang aritmetik.

(a) –5, –3, –1, 1, …

(b) 10, 7, 4, 1, -2, …

(c) 2, 8, 15, 23, …

(d) 3, 6, 12, 24, …

Tip pintar: Bagi suatu janjang aritmetik, anda sentiasa tambah atau tolak satu nombor tetap.

Penyelesaian:

(B) Langkah-langkah untuk membuktikan sama ada jujukan nombor yang diberi ialah satu janjang aritmetik

Langkah 1: Senaraikan tiga sebutan yang berturutan. [Contoh: T₁ , T₂ , T₃.]

Langkah 2: Hitung nilai bagi T₃ − T₂ dan T₂ − T₁ .

Langkah 3: Jika T₃ − T₂ = T₂ − T₁ = d, maka jujukan nombor itu ialah satu janjang aritmetik.

Contoh:

Buktikan sama ada jujukan nombor yang berikut ialah satu janjang aritmetik (J.A.).

(a) 7, 10, 13, …

(b) –20, –15, –9, …

Penyelesaian:

(a)

7, 10, 13 ← (Langkah 1: Senaraikan T₁ , T₂ , T₃)

T₃– T₂ = 13 – 10 = 3 ← (Langkah 2: Cari T₃– T₂ dan T₂ – T₁)

T₂ – T₁ = 10 – 7 = 3 ← (Langkah 2: Cari T₃– T₂ dan T₂ – T₁)

T₃– T₂ = T₂ – T₁

Maka, 7, 10, 13, … ialah J.A.

(b)

–20, –15, –9

T₃– T₂ = –9 – (–15) = 6

T₂ – T₁ = –15 – (–20) = 5

T₃– T₂ ≠ T₂ – T₁

Maka. –20, –15, –9, … bukan satu J.A.