6.2.1 Pythagoras’ Theorem, PT3 Focus Practice
Question 1:
In the diagram, ABC is a right-angled triangle and BCD is a straight line. Calculate the length of AD, correct to two decimal places.
Solution:
In ∆ ABC,
BC2 = 52 – 42
= 25 – 16
= 9
BC = √9
= 3 cm
In ∆ ABD,
BD = BC + CD
= 3 + 6
= 9
AD2 = 42 + 92
= 16 + 81
= 97
AD = √97
= 9.849
= 9.85 cm
Question 2:
In the diagram shows two right-angled triangles. Calculate the perimeter of the whole diagram.
Solution:
In ∆ ABC,
AC2 = 62 + 82
= 36 + 64
= 100
AC = √100
= 10 cm
AD = 5 cm
In ∆ EDC,
EC2 = 122 + 52
= 144 + 25
= 169
EC = √169
= 13 cm
Perimeter of the whole diagram
= AB + BC + CE + DE + AD
= 6 + 8 + 13 + 12 + 5
= 44 cm
Question 3:
Diagram below shows a triangle ACD and ABC is a straight line.
Calculate the length, in cm, of AD.
Solution:
In ∆ DBC,
BC2 = 252 – 242
= 625 – 576
= 49
BC = √49
= 7 cm
AB = 17 – 7 = 10 cm
In ∆ DAB,
AD2 = 102 + 242
= 100 + 576
= 676
AD = √676
= 26 cm
Question 4:
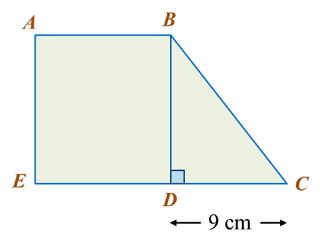
In diagram below ABDE is a square and EDC is a straight line.
The area of the square ABDE is 144 cm2.
Calculate the length, in cm, of BC.
Solution:
BD = √144
= 12 cm
BC2 = 122 + 92
= 144 + 81
= 225
BC = √225
= 15 cm
Question 5:
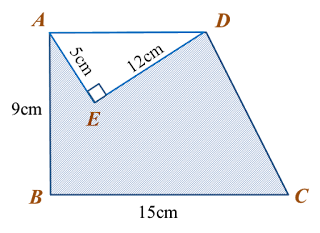
In the diagram, ABCD is a trapezium and AED is a right-angled triangle.
Calculate the area, in cm2, of the shaded region.
Solution:
AD2 = 52 + 122
= 25 + 144
= 169
AD = √169
= 13 cm
Area of trapezium ABDC
= ½ (13 + 15) × 9
= 126 cm2
Area of triangle AED
= ½ × 5 × 12
= 30 cm2
Area of the shaded region
= 126 – 30
= 96 cm2