10.2.1 Circles I, PT3 Focus Practice

10.2.1 Circles I, PT3 Focus Practice

Question 1:

Diagram below shows a circle with centre O.

The radius of the circle is 35 cm.

Calculate the length, in cm, of the major arc AB.

(Use π = \frac{22}{7})

Solution:

Angle of the major arc AB = 360^o – 144^o= 216^o

\begin{array}{l} Length of major arc A B \\ = \frac{216^{o}}{360^{o}} \times 2 π r \\ = \frac{216^{o}}{360^{o}} \times 2 \times \frac{22}{7} \times 35 \\ = 132 cm \end{array}

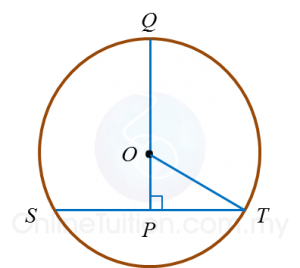
Question 2:

In diagram below, O is the centre of the circle. SPQ and POQ are straight lines.

The length of PO is 8 cm and the length of POQ is 18 cm.

Calculate the length, in cm, of SPT.

Solution:

Radius = 18 – 8 = 10 cm

PT²= 10² – 8²

= 100 – 64

= 36

PT = 6 cm

Length of SPT = 6 + 6

= 12 cm

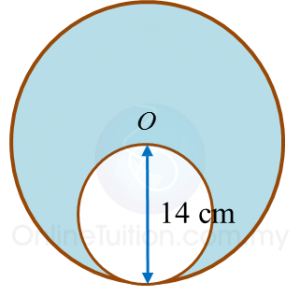
Question 3:

Diagram below shows two circles. The bigger circle has a radius of 14 cm with its centre at O.

The smaller circle passes through O and touches the bigger circle.

Calculate the area of the shaded region.

(Use π = \frac{22}{7})

Solution:

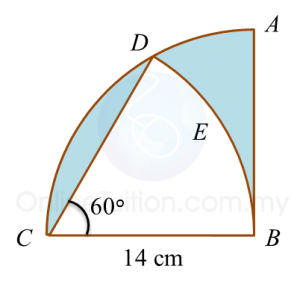
\begin{array}{l} Area of bigger circle = π R^{2} = \frac{22}{7} \times 14^{2} \\ Radius, r of smaller circle = \frac{1}{2} \times 14 = 7 cm \\ Area of smaller circle = π r^{2} = \frac{22}{7} \times 7^{2} \\ ∴ Area of shaded region \\ = (\frac{22}{7} \times 14^{2}) - (\frac{22}{7} \times 7^{2}) \\ = 616 - 154 \\ = 462 {cm}^{2} \end{array}

Question 4:

Diagram below shows two sectors. ABCD is a quadrant and BED is an arc of a circle with centre C.

Calculate the area of the shaded region, in cm².

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} The area of sector C B E D \\ = \frac{60^{o}}{360^{o}} \times π r^{2} \\ = \frac{60^{o}}{360^{o}} \times \frac{22}{7} \times 14^{2} \\ = 102 \frac{2}{3} {cm}^{2} \end{array}

\begin{array}{l} The area of quadrant A B C D \\ = \frac{1}{4} \times π r^{2} \\ = \frac{1}{4} \times \frac{22}{7} \times 14^{2} \\ = 154 {cm}^{2} \end{array}

\begin{array}{l} Area of the shaded region \\ = 154 - 102 \frac{2}{3} \\ = 51 \frac{1}{3} {cm}^{2} \end{array}

Question 5:

Diagram below shows a square KLMN. KPN is a semicircle with centre O.

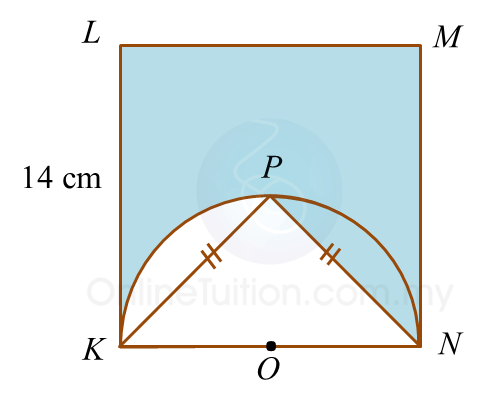
Calculate the perimeter, in cm, of the shaded region.

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} K O = O N = O P = 7 cm \\ P N = \sqrt{7^{2} + 7^{2}} \\ = \sqrt{98} \\ = 9.90 cm \\ Arc length K P \\ = \frac{1}{4} \times 2 \times \frac{22}{7} \times 7 \\ = 11 cm \end{array}

Perimeter of the shaded region

= KL + LM + MN + NP + Arc length PK

= 14 + 14 +14 + 9.90 + 11

= 62.90 cm