Home › PT3 Maths › 11.1 Transformations (I)

11.1 Transformations (I)

Posted on by

11.1 Transformations (I)

11.1.1 Transformation
A transformation is a one-to-one correspondence or mapping between points of an object and its image on a plane. 


11.1.2 Translation
1. A translation is a transformation which moves all the points on a plane through the same distance in the same direction.
 
2. Under a translation, the shape, size and orientation of object and its image are the same.
 
3. A translation in a Cartesian plane can be represented in the form ( a b ) ,  whereby, a represents the movement to the right or left which is parallel to the x-axis and b represents the movement upwards or downwards which is parallel to the y-axis.

Example 1:
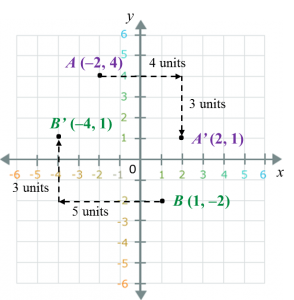
Write the coordinates of the image of A (–2, 4) under a translation ( 4 − 3 )  and B (1, –2) under a translation ( − 5 3 ) .

Solution:
 
A’ = [–2 + 4, 4 + (–3)] = (2, 1)
B’ = [1 + (–5), –2 + 3] = (–4, 1)

Example 2:
Point K moved to point K’ (3, 8) under a translation ( − 4 3 ) .  
What are the coordinates of point K?

Solution:
K ( x , y ) → ( − 4 3 ) → K ' ( 3 , 8 )
The coordinates of K = [3 – (– 4), 8 – 3]
= (7, 5)

Therefore the coordinates of K are (7, 5).



11.1.3 Reflection
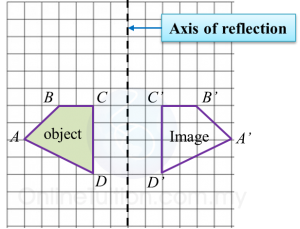
1. A reflection is a transformation which reflects all points of a plane in a line called the axis of reflection.
2. In a reflection, there is no change in shape and size but the orientation is changed. Any points on the axis of reflection do not change their positions.

Example 3:

11.1.4 Rotation
1. A rotation is a transformation which rotates all points on a plane about a fixed point known as the centre of rotation through a given angle in a clockwise or anticlockwise direction.
2. In a rotation, the shape, size and orientation remain unchanged.
3. The centre of rotation is the only point that does not change its position.

Example 4:
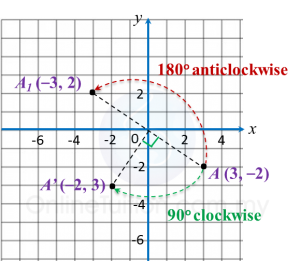
Point A (3, –2) is rotated through 90o clockwise to A’ and 180o anticlockwise to A1 respectively about origin.
State the coordinates of the image of point A.

Solution:
Image A’ = (–2, 3)
Image A1 = (–3, 2) 


11.1.5 Isometry
1. An isometry is a transformation that preserves the shape and size of an object.
2.Translation, reflection and rotation and a combination of it are isometries.


11.1.6 Congruence
1. Congruent figures have the same size and shape regardless of their orientation.
2. The object and the image obtained under an isometry are congruent.