Question 1:
Diagram 1.1 shows the process of latex coagulation.

(a)(i) State one example of chemical P? [1 mark]
(ii) State one characteristic of coagulated latex in Diagram 1.1. [1 mark]
(b) Chemical P in diagram 1.1 is replaced with chemical Q to prevent latex from coagulating.
State one example of chemical Q. [1 mark]
(c) Diagram 1.2 shows the process when natural rubber is heated with Sulphur to form rubber R.

(i) Name process X. [1 mark]
(ii) Name rubber R. [1 mark]
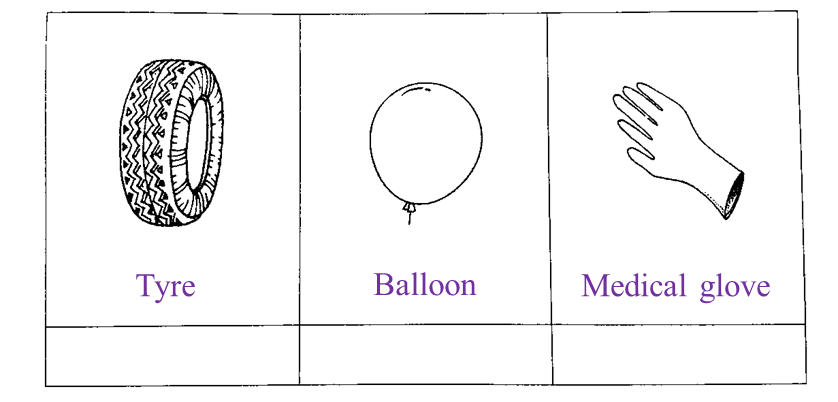
(d) Mark (\/) the object which is made of rubber R. [1 mark]
Answer:
(a)(i) Methanoic acid
(a)(ii) Elastic
(b) Ammonia solution
(c)(i) Vulcanization of rubber
(c)(ii) Vulcanized rubber
(d)
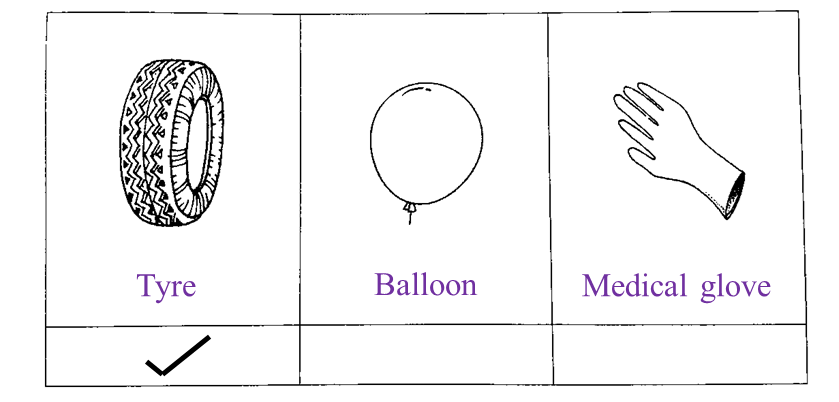
Diagram 1.1 shows the process of latex coagulation.

(a)(i) State one example of chemical P? [1 mark]
(ii) State one characteristic of coagulated latex in Diagram 1.1. [1 mark]
(b) Chemical P in diagram 1.1 is replaced with chemical Q to prevent latex from coagulating.
State one example of chemical Q. [1 mark]
(c) Diagram 1.2 shows the process when natural rubber is heated with Sulphur to form rubber R.

(i) Name process X. [1 mark]
(ii) Name rubber R. [1 mark]
(d) Mark (\/) the object which is made of rubber R. [1 mark]

Answer:
(a)(i) Methanoic acid
(a)(ii) Elastic
(b) Ammonia solution
(c)(i) Vulcanization of rubber
(c)(ii) Vulcanized rubber
(d)

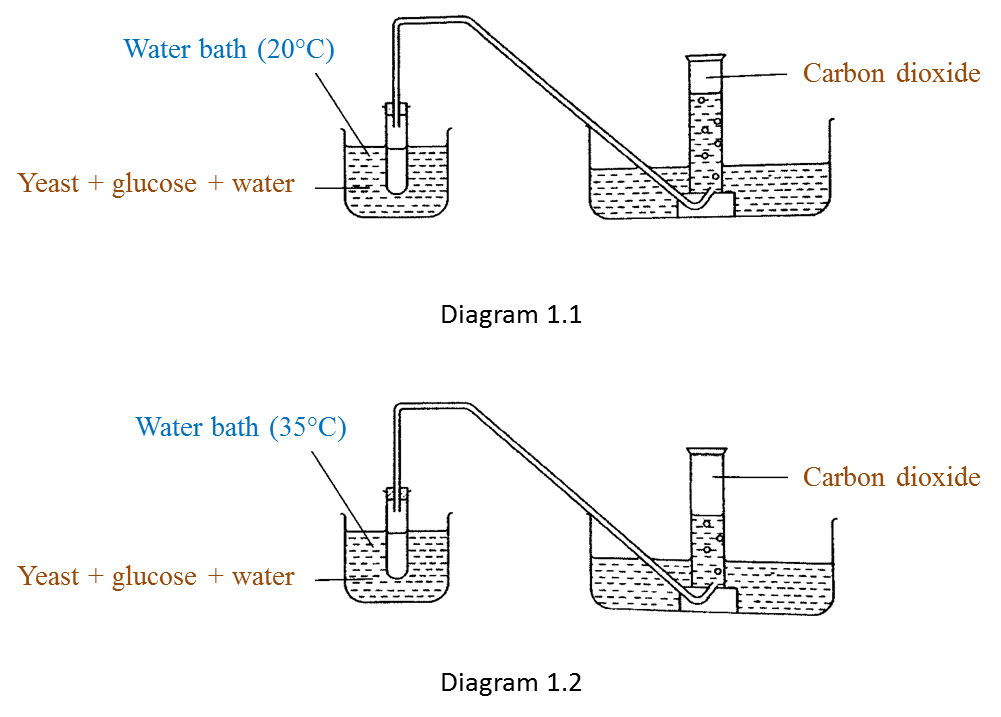
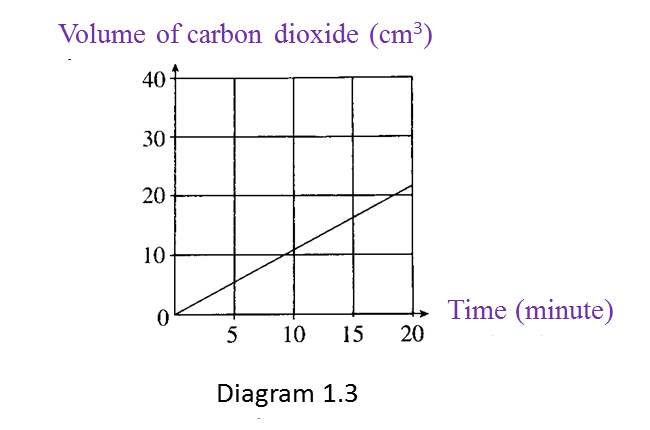 What is the relationship between the volume of carbon dioxide produced and time? [1 mark]
What is the relationship between the volume of carbon dioxide produced and time? [1 mark]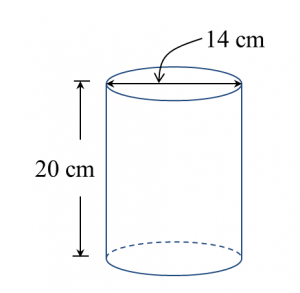
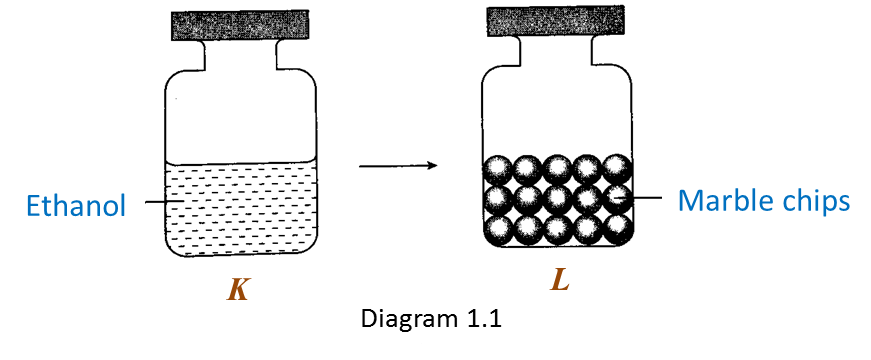
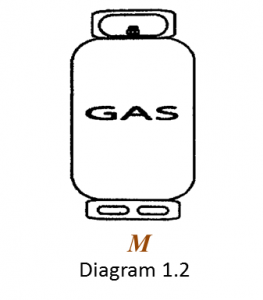 (i) State two elements present in gas M. [1 mark]
(i) State two elements present in gas M. [1 mark]
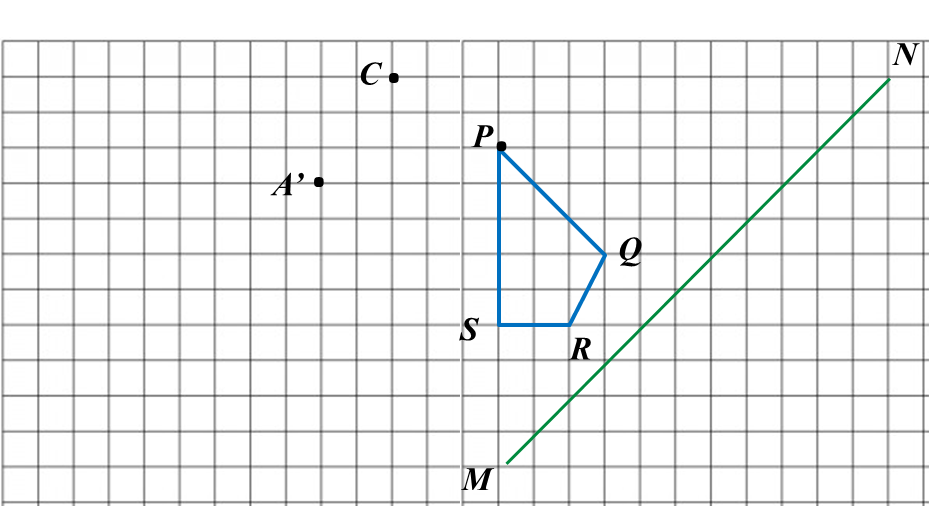
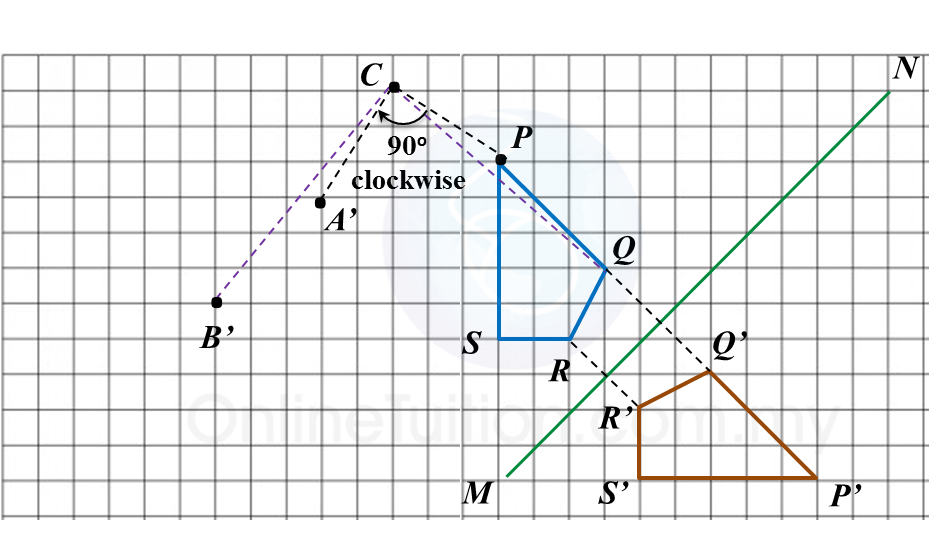
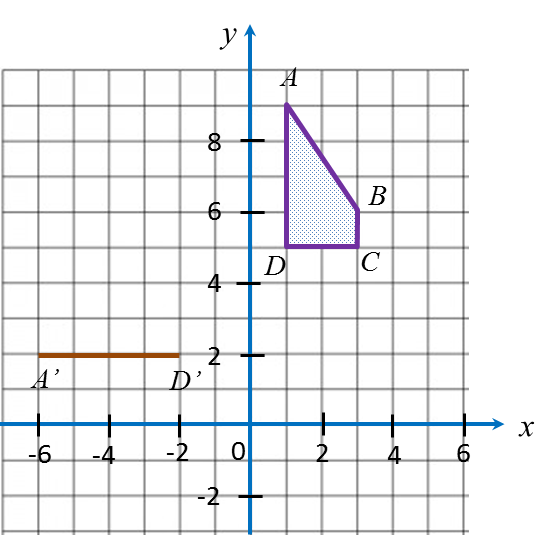
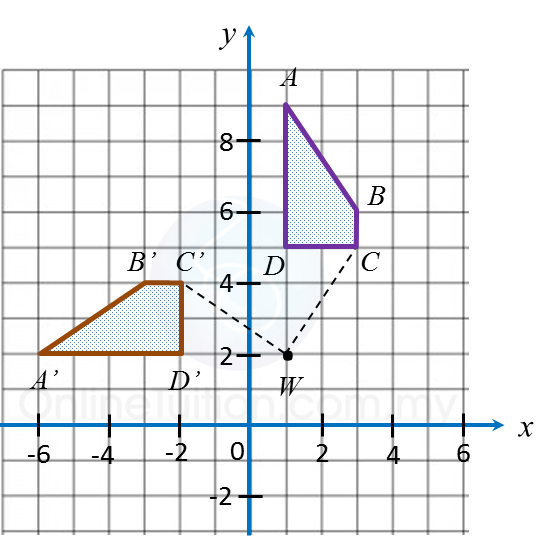
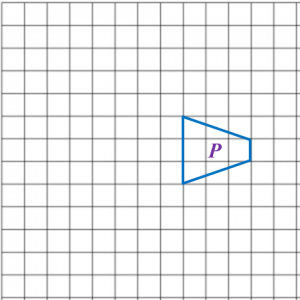
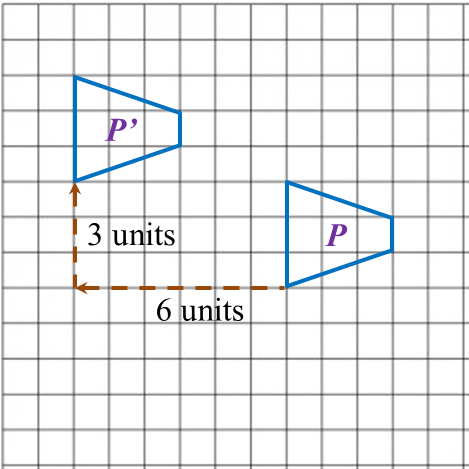
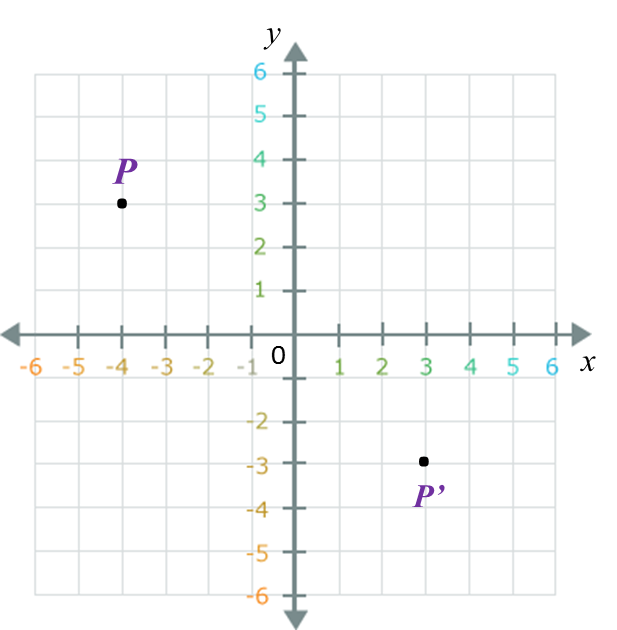

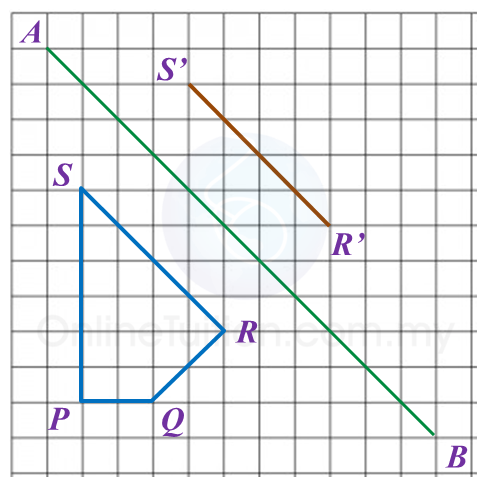

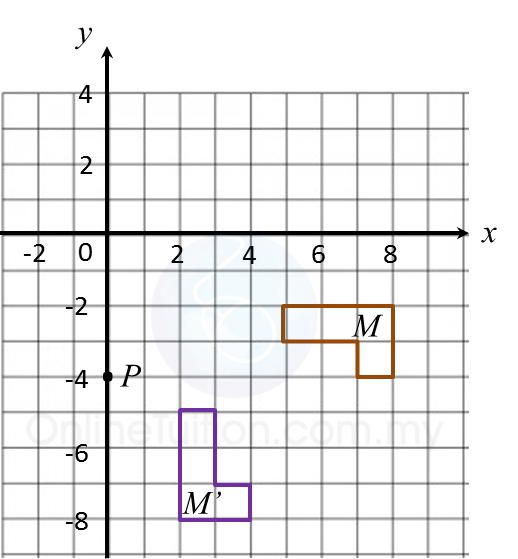
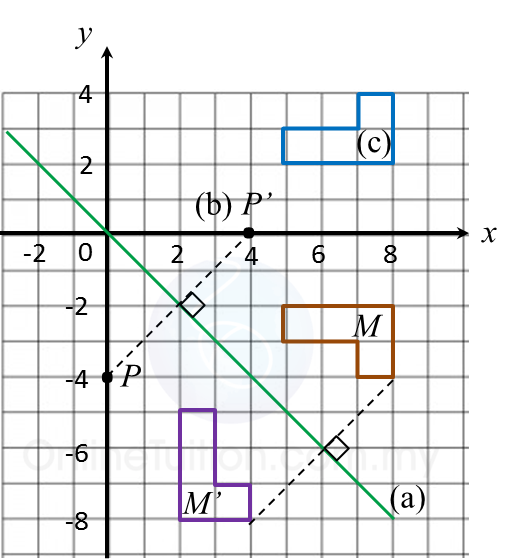
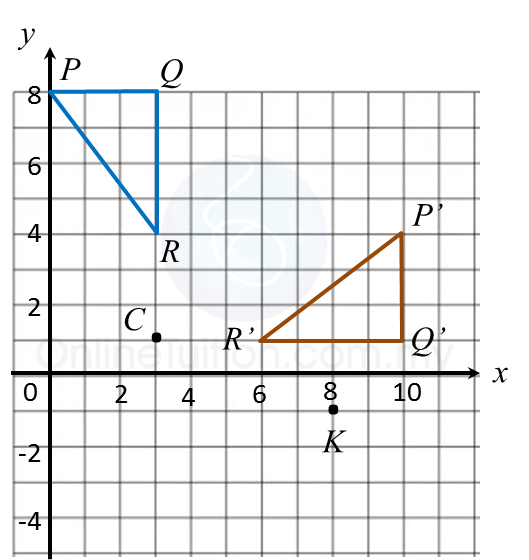
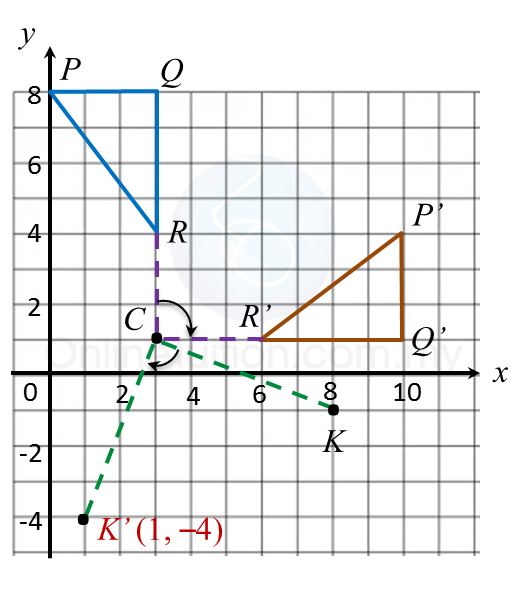
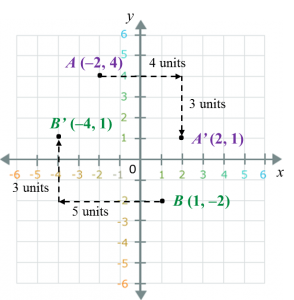
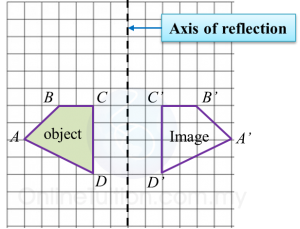
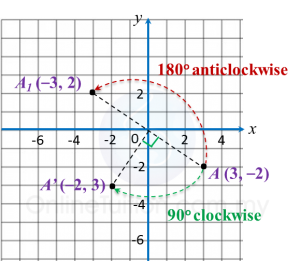
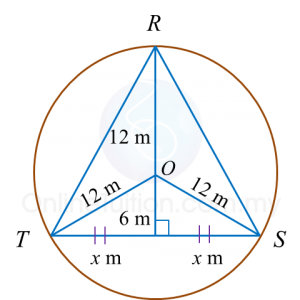
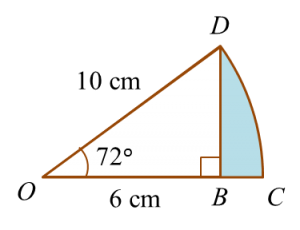
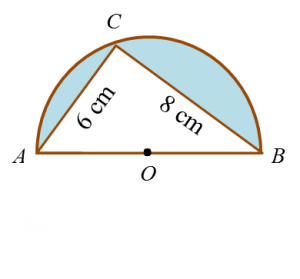
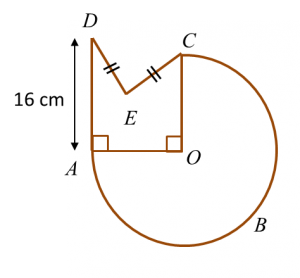
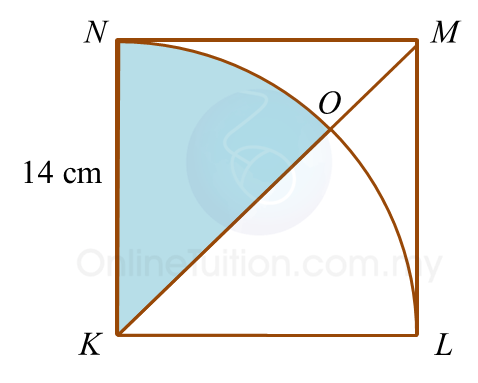
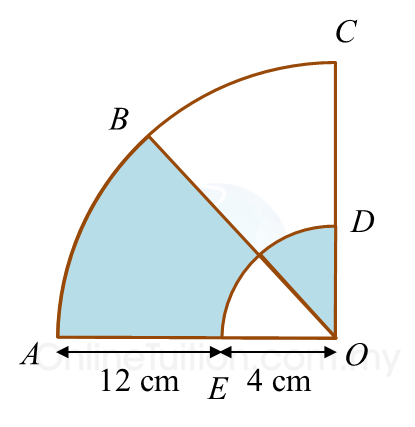
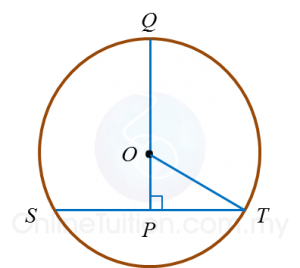
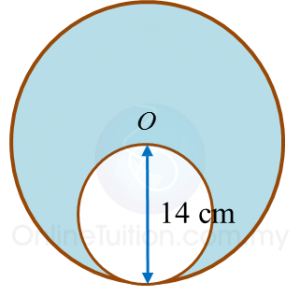
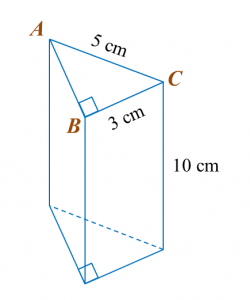
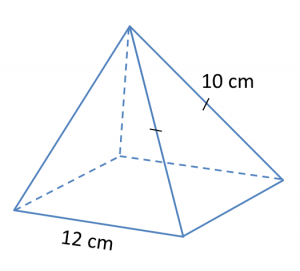
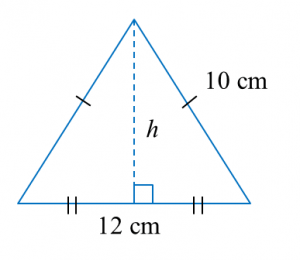
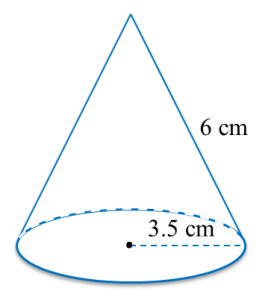
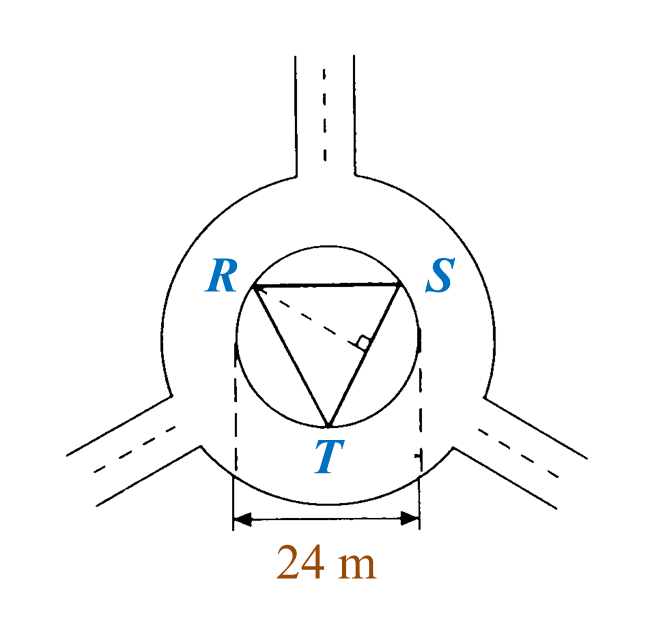 Find the perimeter of the platform.
Find the perimeter of the platform.