Question 11:
Diagram below shows two baskets of eggs.

(a) State the ratio of the number of chicken eggs to the number of duck eggs.
(b) A number of eggs need to be added into each basket so that the ratio in (a) remain unchanged. Find the minimum number of eggs to be added in each basket.
Solution:
(a)
Ratio of the number of chicken eggs to the number of duck eggs
= 12 : 16
= 3 : 4
(b)
Let the number of eggs need to be added into each basket =
n
Total number of eggs need to be added into each basket
= 3
n + 4
n
Minimum value of
n = 1
Hence, the minimum number of eggs to be added into each basket
= 3(1) + 4(1)
= 3 + 4
= 7 (3 chicken eggs and 4 duck eggs need to be added to each basket)
Question 12:
Diagram below shows two baskets,
A and
B, filled with candies.
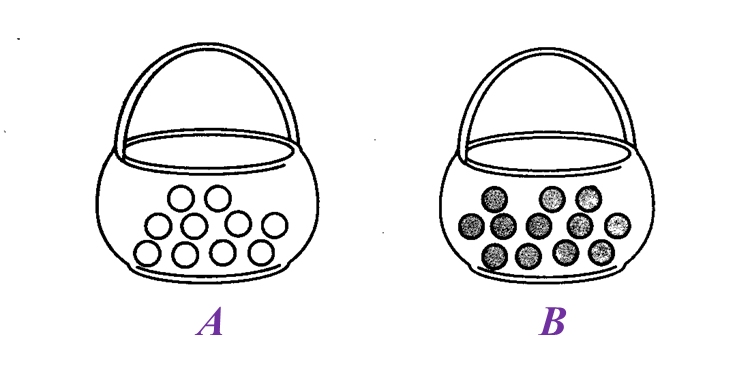
(a) State the ratio of the number of candies in basket
A to the number of candies in basket
B.
(b) If 20 candies are added into basket
A, calculate the number of candies which need to be added into basket
B so that the ratio in (a) remain unchanged.
Solution:
(a)
Ratio of the number of candies in basket
A to the number of candies in basket
B
= 10 : 12
= 5 : 6
(b)
If 20 candies are added into basket
A, the number of candies which need to be added into basket
B so that the ratio 5 : 6 remain unchanged
= 20 ÷ 5 × 6
= 4 × 6
= 24
Question 13:
Karim built two towers using toy bricks of the same size as shown in Diagram below.
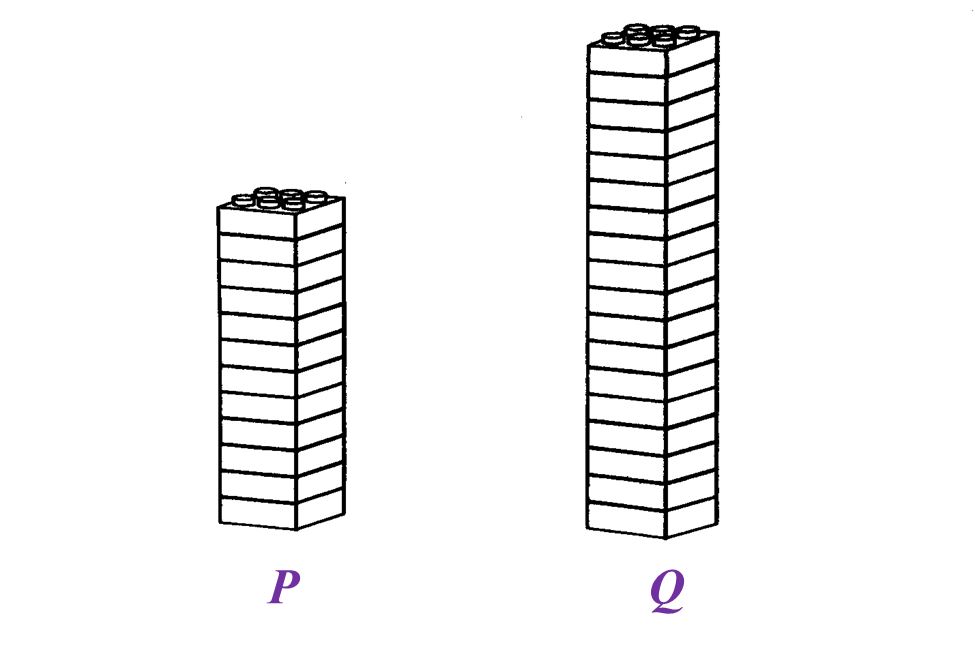
(a) State the ratio of the number of toy bricks in Tower
P to the number of toy bricks in Tower
Q.
(b) A number of toy bricks need to be removed from each tower so that the ratio in (a) remains unchanged.
Find the total number of toy bricks to be removed from each tower.
Solution:
(a)
Tower
P : Tower
Q
= 12 : 18
= 2 : 3
(b)
Let number of toy bricks to be removed from each tower =
n
Total number of bricks to be removed
= 2
n + 3
n
2(1) + 3(1) = 2 + 3 =
5 → (2 bricks from tower
P, 3 bricks from tower
Q)
2(2) + 3(2) = 4 + 6 =
10 → (4 bricks from tower
P, 6 bricks from tower
Q)
2(3) + 3(3) = 6 + 9 =
15 → (6 bricks from tower
P, 9 bricks from tower
Q)
2(4) + 3(4) = 8 + 12 =
20 → (8 bricks from tower
P, 12 bricks from tower
Q)
2(5) + 3(5) = 10 + 15 =
25 → (10 bricks from tower
P, 15 bricks from tower
Q)

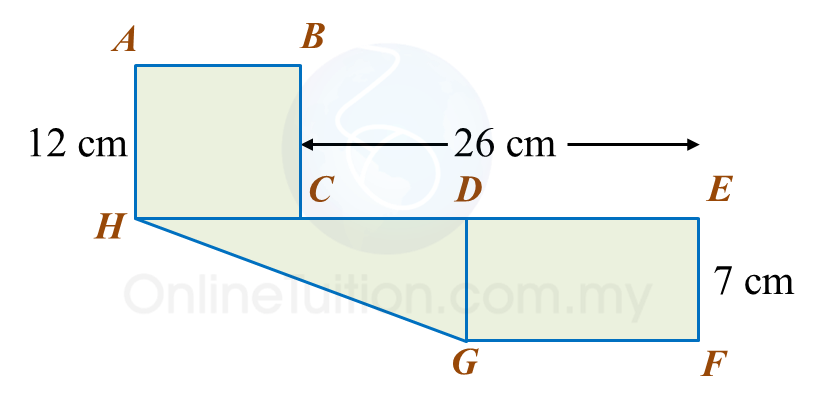

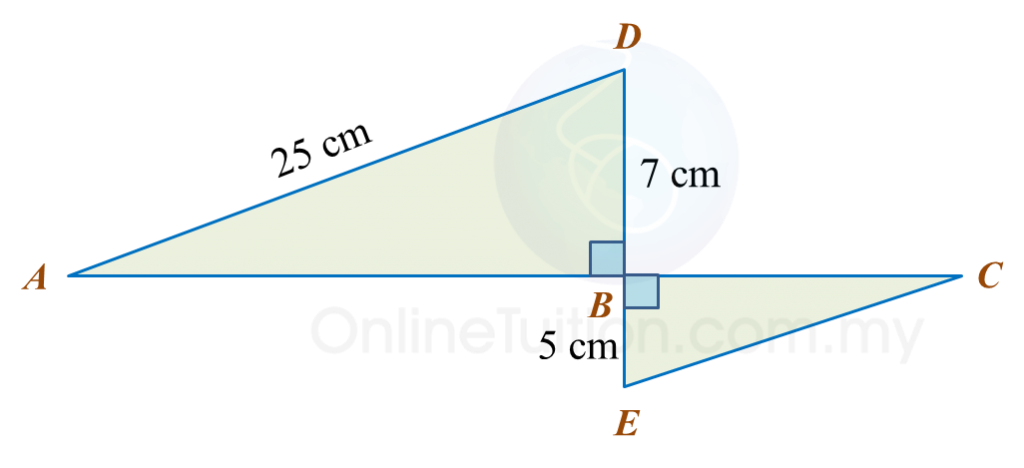
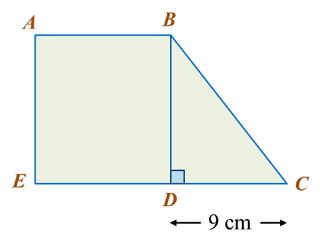
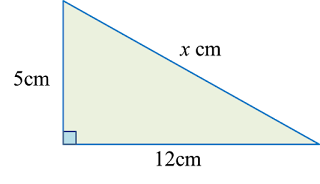
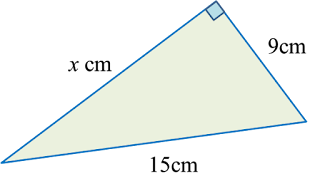
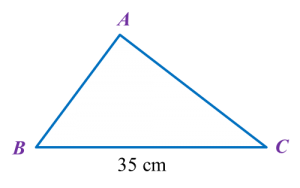
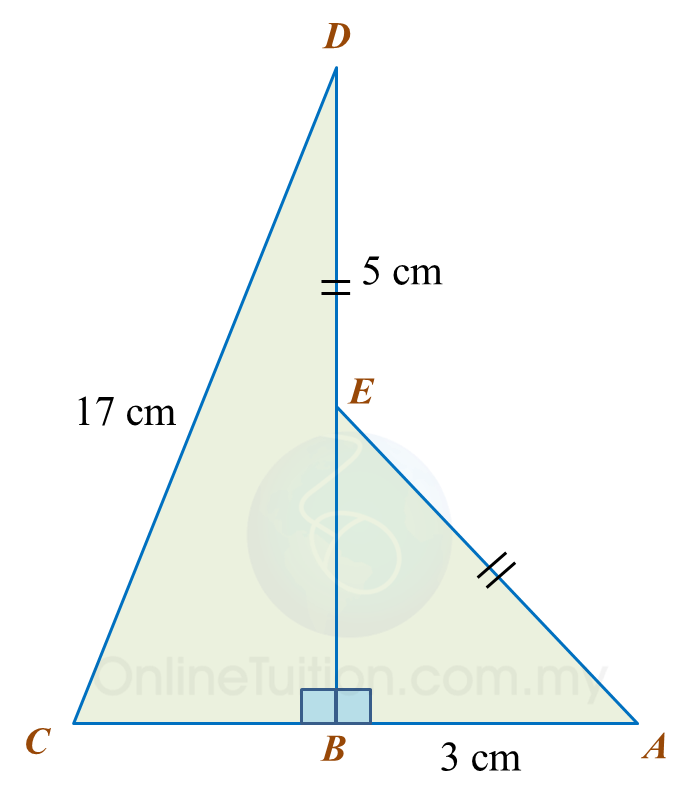 Find the length, in cm, of BC. Round off the answer to two decimal places.
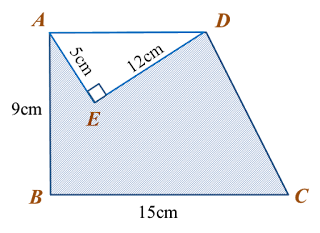
Find the length, in cm, of BC. Round off the answer to two decimal places.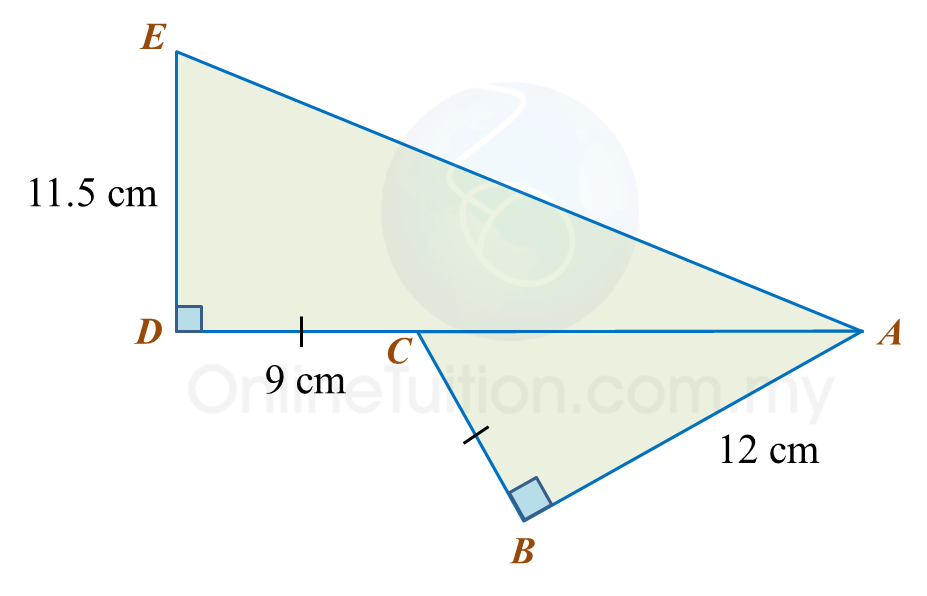 Find the length, in cm, of AE. Round off the answer to one decimal places.
Find the length, in cm, of AE. Round off the answer to one decimal places.



 (a) State the ratio of the number of chicken eggs to the number of duck eggs.
(a) State the ratio of the number of chicken eggs to the number of duck eggs. (a) State the ratio of the number of candies in basket A to the number of candies in basket B.
(a) State the ratio of the number of candies in basket A to the number of candies in basket B. (a) State the ratio of the number of toy bricks in Tower P to the number of toy bricks in Tower Q.
(a) State the ratio of the number of toy bricks in Tower P to the number of toy bricks in Tower Q.
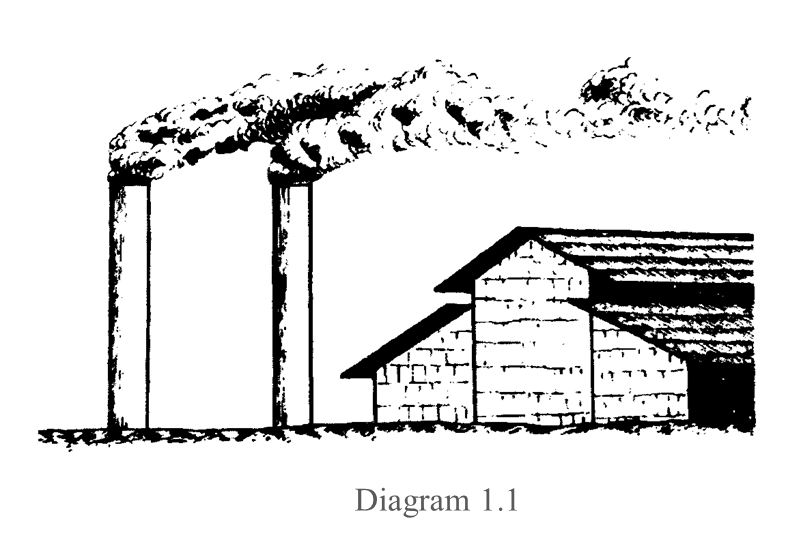
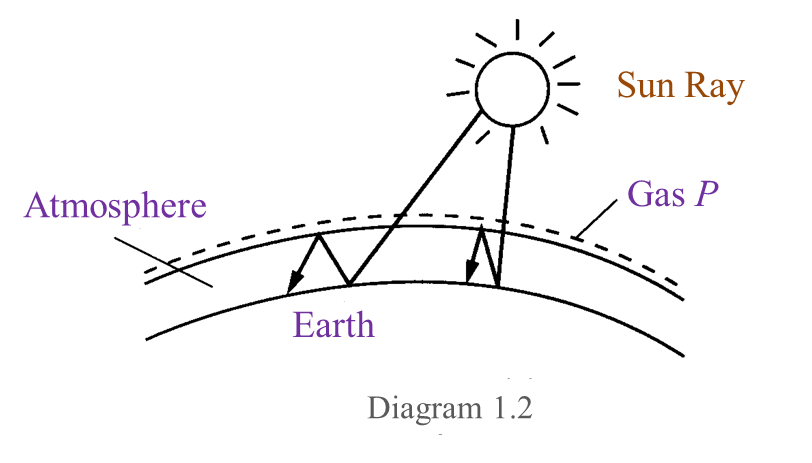 (i) Name gas P. [1 mark]
(i) Name gas P. [1 mark]