1.1 Directed Numbers
1.1.1 Multiplication and Division of Integers
1. Multiplication and division of like signs gives (+)
2. Multiplication and division of unlike signs gives (–)
Example:
(a) –25 ÷ 5 = –5
(b) 8 × (–5) = –40
3. Multiplication of 3 integers.
4. Division of 3 integers.
5. The product of an integer and zero is always zero.
Example:
–5 × 0 = 0
6. When zero is divided by any integer except zero, the quotient is zero. Any integer divided by zero is undefined.
Example:
(a) 0 ÷ 9 = 0
(b) –6 ÷ 0 is undefined
1.1.2 Combined Operations of Integers
1. BODMAS → (Brackets of Division, Multiplication, Addition and Subtraction)
|
1. Operations in the brackets should be carried out first.
2. Followed by × or ÷ from left to right.
3. Followed by + or – from left to right.
|
Example 1:
(a) –52 ÷ 13 – 15 × 4
(b) 63 ÷ (16 – 7) × (–2)
(c) –30 + 9 × 7 – 16
Solution:
(a)
–52 ÷ 13 – 15 × 4
= (–52 ÷ 13) – (15 × 4) ← (calculate from left to right; ÷ and × are done first)
= –4 – 60
= –64
(b)
63 ÷ (16 – 7) × (–2)
= 63 ÷ 9 × (–2) ← (bracket is done first, then work from left to right)
= 7 × (–2)
= –14
(c)
–30 + 9 × 7 – 16
= –30 + (9 × 7) – 16 ← ( multiply first)
= –30 + 63 – 16
= 17
1.1.3 Fractions
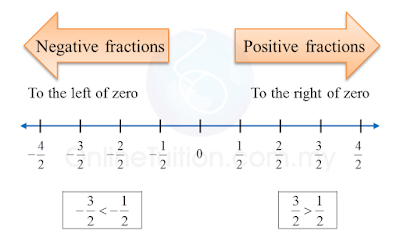
1. Positive fractions are fractions with the positive sign (+), and their values are greater than 0.
2. Negative fractions are fractions with the negative sign (–), and their values are less than 0.1.1.4 Decimals
1. There are positive decimals and negative decimals.
2. Positive decimals are greater than zero and negative decimals are less than zero.1.1.5 Directed Numbers
1. Integers, fractions and decimals are directed numbers.
2.The computations of directed numbers is the same as that for whole numbers.
Example 2:
(a)
(b) [(–28) – (–4)] ÷ (–5.147 – 0.853)
Solution:
(a)
(b)
[(–28) – (–4)] ÷ (–5.147 – 0.853)
= [–28 + 4] ÷ (–6)
= (–24) ÷ (–6)
= 4

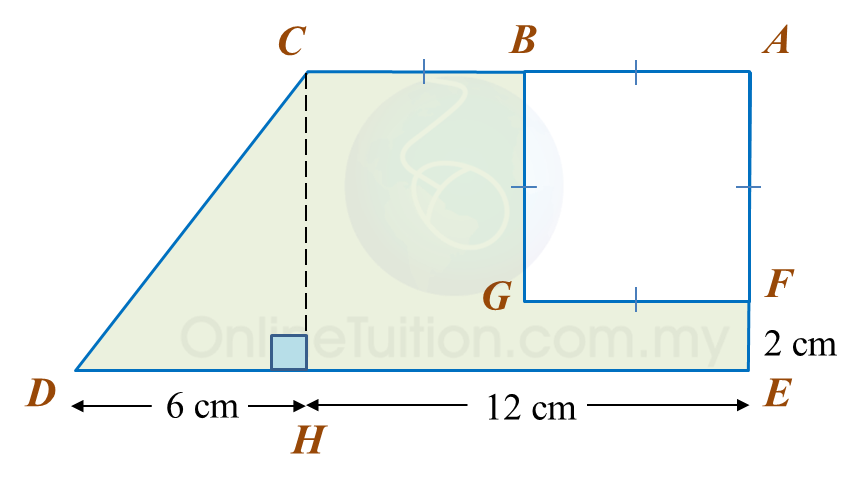
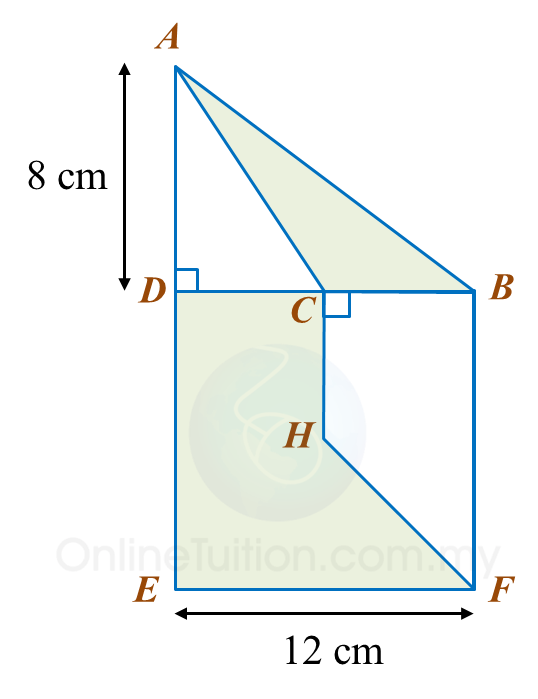 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.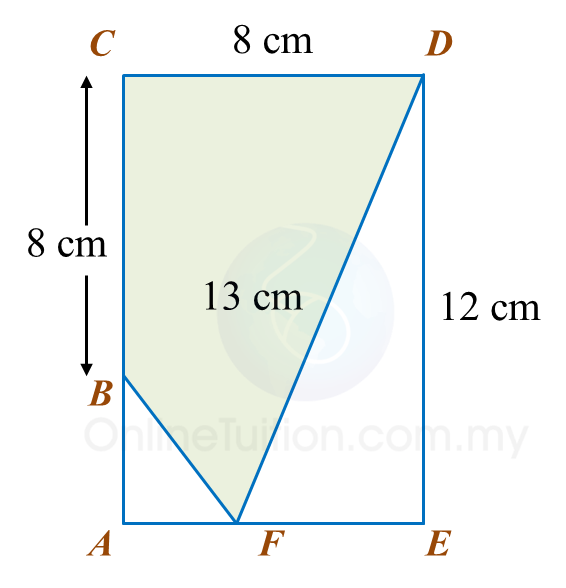
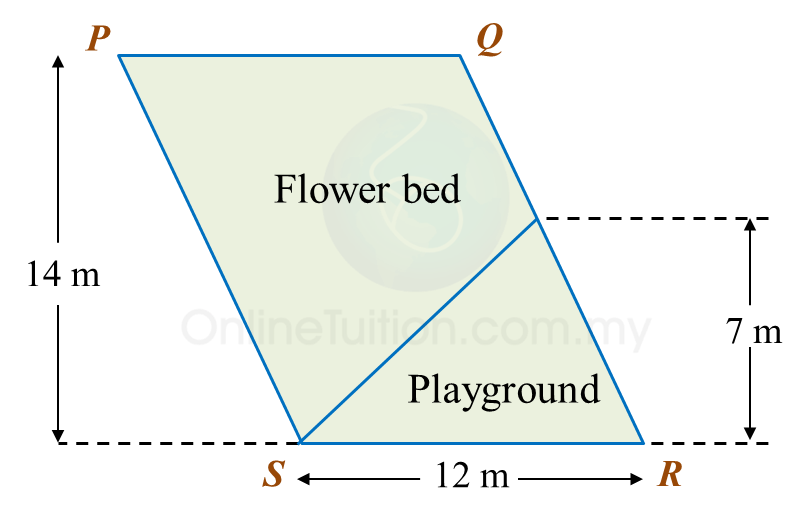 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.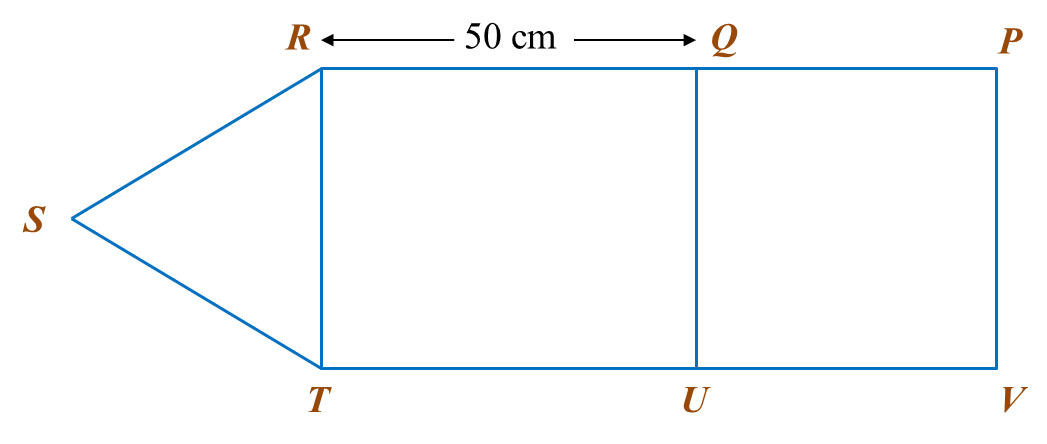
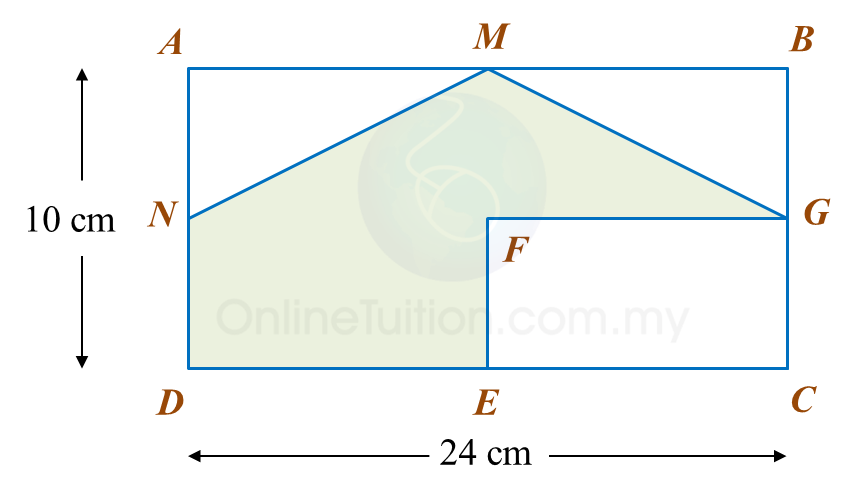
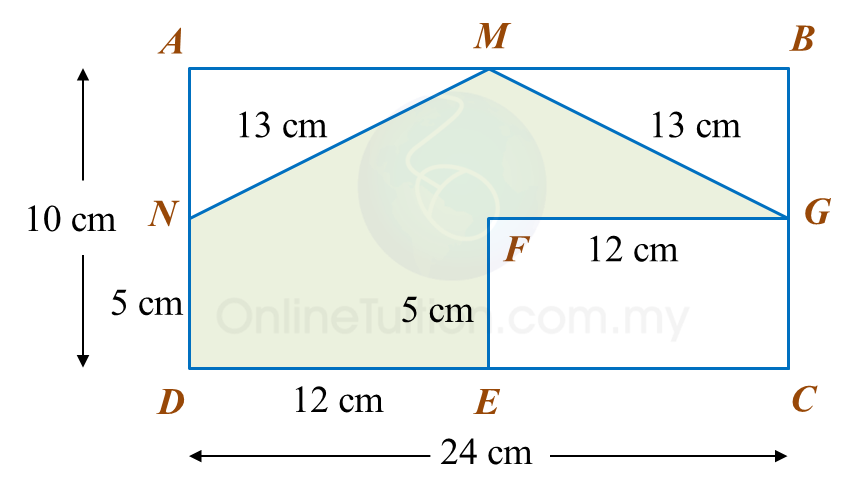
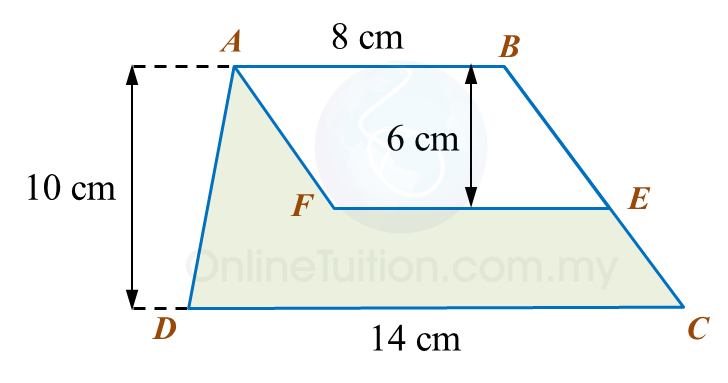
 The area of ABEF is 72 cm2.
The area of ABEF is 72 cm2.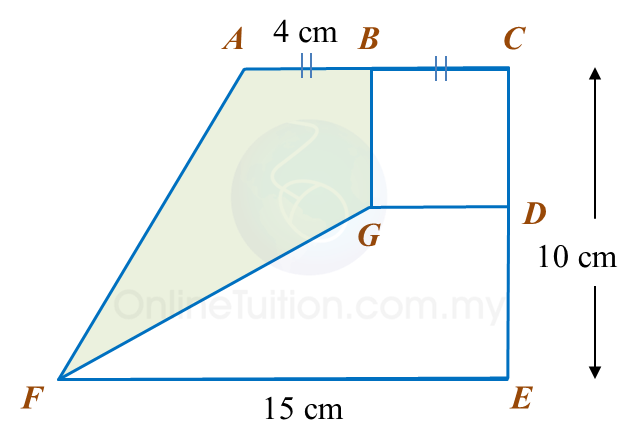
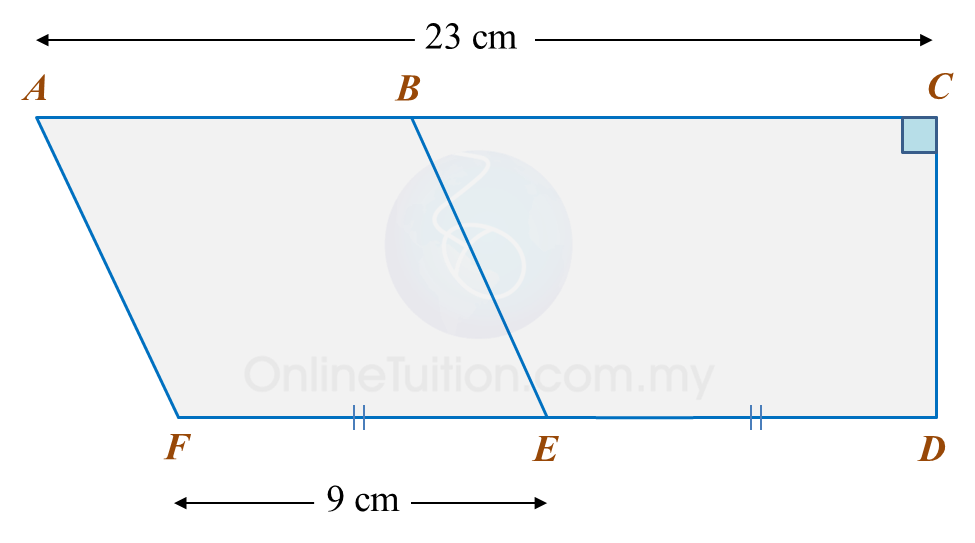
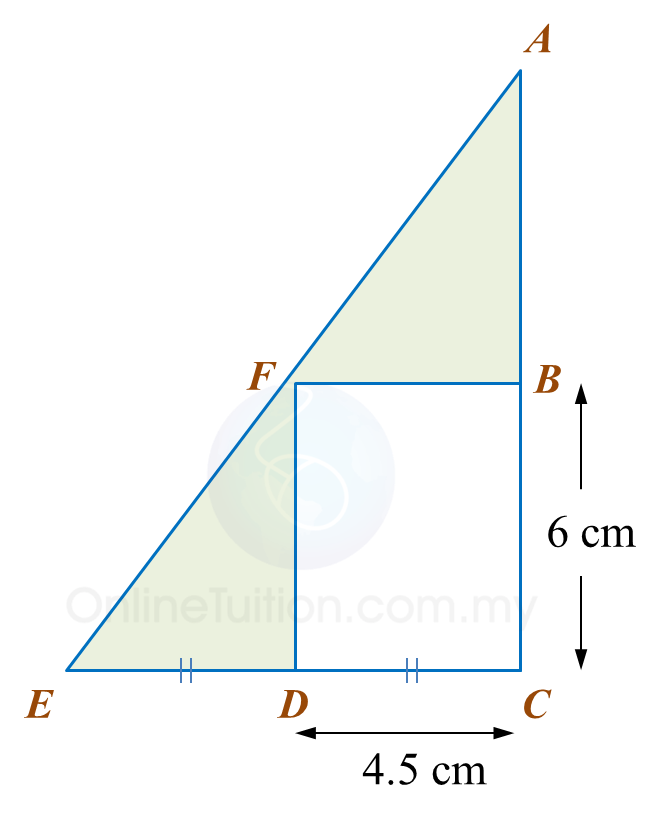
 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
 Calculate
Calculate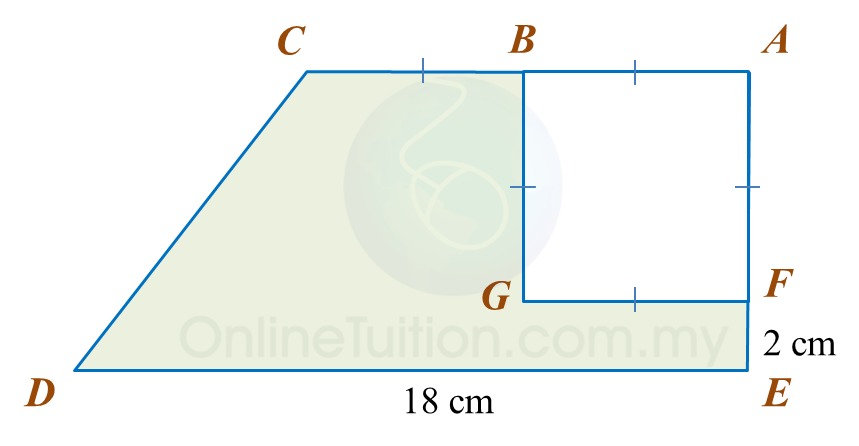




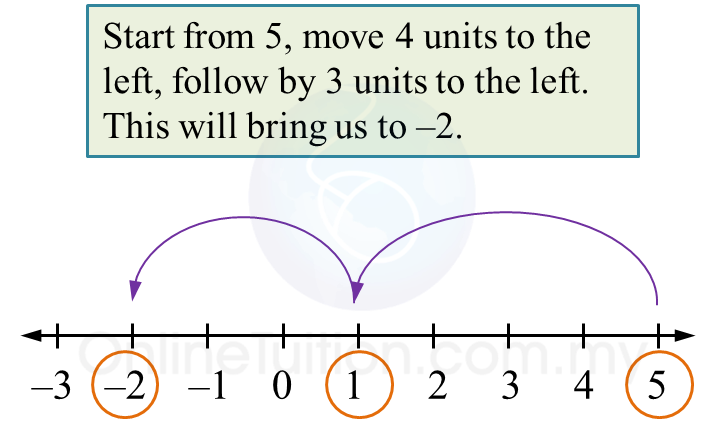

 Therefore,
Therefore, Therefore,
Therefore,