5.2.2 Percentages, PT3 Practice

Posted on March 7, 2017 by user

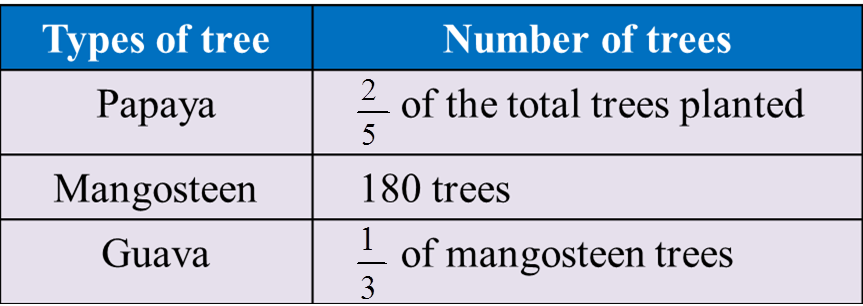
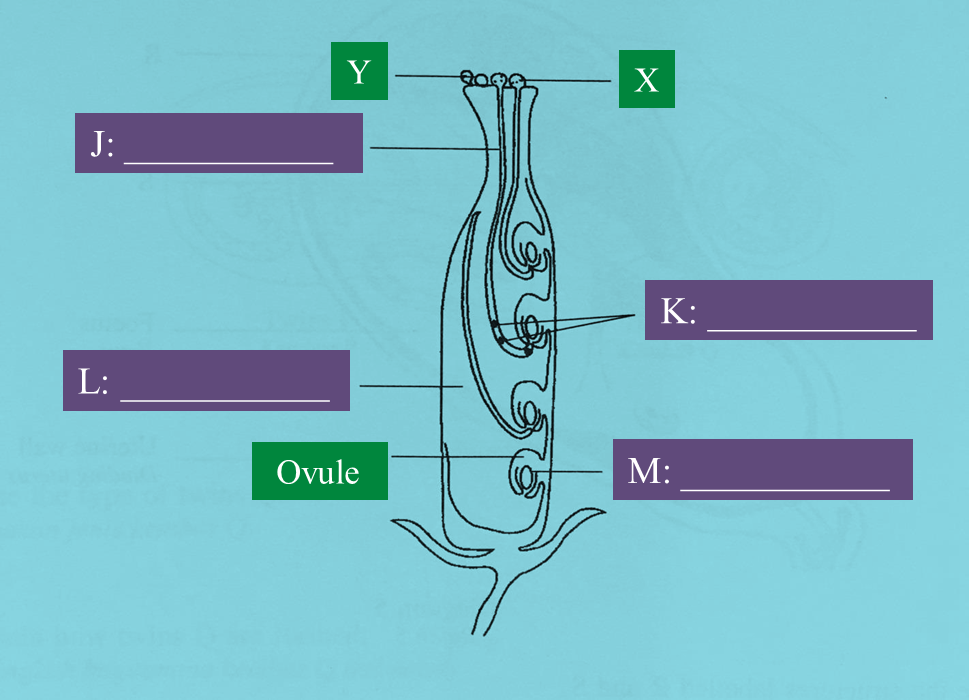
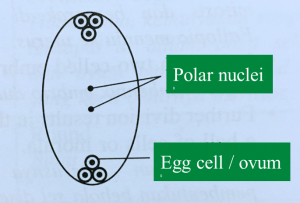
Question 6:
Liza had 360 apples. She sold ⅝ of the apples. Then she gave 27 of the remaining apples to her neighbour.
Calculate the percentage of apples that Liza has left.

Solution:

\begin{array}{l} Number of apples sold \\ = \frac{5}{8} \times 360 \\ = 225 \\ Number of apples left \\ = 360 - 225 - 27 \\ = 108 \\ Percentage of apples left \\ = \frac{108}{360} \times 100 % \\ = 30 % \end{array}

Question 7:
Mei Ling took part in a science quiz competition. She answered 12 questions correctly. She answered 25% of the questions incorrectly.
Find the total number of questions in the quiz.

Solution:

\begin{array}{l} 75 % \to 12 correct answers \\ 25 % \to ? incorrect answers \\ Number of incorrect answers \\ = \frac{25}{75^{3}} \times 12 \\ = 4 \\ Total number of questions \\ = 12 + 4 \\ = 16 \end{array}

Question 8:
Diagram below shows the prices of two items.

Kenny buys a pair of track pants and 2 pieces of sweaters.
Calculate the total amount Kenny has to pay.

Solution:

\begin{array}{l} Price of a pair of track pants after 25% discount \\ = RM 150.00 - (\frac{25}{100} \times RM 150.00) \\ = RM 150.00 - RM37 .50 \\ = RM 112.50 \\ Total amount Kenny has to pay \\ = (RM 100.00 \times 2) + RM 112.50 \\ = RM3 12.50 \end{array}

Question 9:
Table below shows the prices and the discounts for the same brand of school bag sold at four shops, P, Q, R and S.

Which shop offers the cheapest price?

Solution:

\begin{array}{l} Shop P, \\ Price per item after discount \\ = RM 100 - (\frac{20}{100} \times RM 100) \\ = RM 80 \\ Shop Q, \\ Price per item after discount \\ = RM 110 - (\frac{30}{100} \times RM 110) \\ = RM77 \\ Shop R, \\ Price per item with no discount \\ = RM 170 \div 2 \\ = RM85 \\ Shop S, \\ Price per item with no discount = RM90 \\ Shop Q offers the cheapest price . \end{array}

Question 10:
Table below shows dividend received by Janice from her investment.

Janice reinvests RM204 from the total dividends she received into ASB investment.
What is the remaining percentage that she did not use in her reinvestment?

Solution:

\begin{array}{l} Dividends from ASB \\ = 3 % \times RM 2 000 \\ = \frac{3}{100} \times RM 2 000 \\ = RM 60 \\ Dividends from ASN \\ = 4 % \times RM 7 000 \\ = \frac{4}{100} \times RM 7 000 \\ = RM 280 \\ Total dividends \\ = RM 60 + RM 280 \\ = RM 340 \\ Percentage of dividends not reinvested \\ = \frac{340 - 204}{340} \times 100 \\ = \frac{136}{340} \times 100 \\ = 40 % \end{array}

5.2.1 Percentages, PT3 Practice

Posted on March 5, 2017 by user

Question 1:
Rahman bought a house at RM180 000. The market price of the house increases by 15 % per year. After a year, Rahman sold his house at the price of RM 205 000.
Is the selling price higher compared to the market price? Show your working.

Solution:

\begin{array}{l} Market price \\ = 115 % \times RM180 000 \\ = \frac{115}{100} \times RM180 000 \\ = RM 207 000 \\ RM 207 000 > RM 205 000 \\ The market price of the house is higher than the selling price of the house . \end{array}

Question 2:
A company makes a profit of RM 50 000 in year 2016. The projection of profit increase is fixed at 20 % from the previous year.
Predict the company profit in year 2018.

Solution:

\begin{array}{l} Profit in year 2017 \\ = RM 50 000 \times \frac{120}{100} \\ = RM6 0 000 \\ Profit in year 2018 \\ = RM6 0 000 \times \frac{120}{100} \\ = RM72 000 \end{array}

Question 3:
Sharon wants to buy a new car with the price of RM 78 500. Her father gives her some money, which is 30 % of the car price. The deposit for the car is

\frac{1}{5}

of the price.
Would her father’s contribution be enough for her deposit? Give your reason with calculation.

Solution:

\begin{array}{l} 30 % of the car price given by Sharon's father \\ = \frac{30}{100} \times RM 78500 \\ = RM 235 50 \\ Deposit of the car price needed \\ = \frac{1}{5} \times RM 78500 \\ = RM 15700 \\ RM 235 50 > RM 15700, therefore her father 's contribution is \\ enough for the deposit . \end{array}

Question 4:
The profit of Company P and Company Q in March are RM38 000 and RM48 000 respectively. In April, the profit of Company P has increased by 20%.
Given the profit for both companies are equal in April, find the percentages decrease in profit of Company Q.

Solution:

\begin{array}{l} Profit of Company P in April \\ = \frac{120}{100} \times 38000 \\ = RM45600 \\ Drop in profit of Company Q \\ = RM48000 - RM45600 \\ = RM24 00 \\ Percentage decrease in profit \\ = \frac{2400}{48000} \times 100 % \\ = 5 % \end{array}

Question 5:
A biscuit making company needs 200 tonnes of flour every month. Factory K supplies 80 tonnes, while the rest is supplied by Factory M. In a particular month, Factory K faces a problem which forces it to reduce its output by 15%.
Find the total percentage of the flour output of Factory M in order to accommodate the requirement of the biscuit making company.

Solution:

\begin{array}{l} New flour supply from Factory K \\ = \frac{85}{100} \times 80 \\ = 68 tonnes \\ New flour supply from Factory M \\ = 200 - 68 \\ = 132 tonnes \\ Total percentage of flour output of Factory M \\ = \frac{132}{120} \times 100 % \\ = 110 % \end{array}

4.2.2 Decimals, PT3 Practice

Posted on February 22, 2017 by user

Question 5:
Calculate the value of

\frac{4}{5} + 15.4 \div 4

and express the answer correct to one decimal place.

Solution:

\begin{array}{l} \frac{4}{5} + 15.4 \div 4 \\ = \frac{4}{5} + 3.85 \\ = 0.8 + 3.85 \\ = 4.65 \\ = 4.7 (one decimal place) \end{array}

Question 6:
Calculate the value of 84 – 3(14 + 48 ÷ 6) =

Solution:

\begin{array}{l} 84 - 3 (14 + 48 \div 6) \\ = 84 - 3 [14 + (48 \div 6)] \\ = 84 - 3 (14 + 8) \\ = 84 - 3 (22) \\ = 84 - 66 \\ = 18 \end{array}

Question 7:

Calculate the value of \frac{4 \times 0.18}{0.9} .

Solution:

\begin{array}{l} \frac{4 \times 0.18}{0.9} = \frac{0.72}{0.9} \\ = \frac{0.72 \times 10}{0.9 \times 10} \\ = \frac{7.2}{9} \\ = 0.8 \end{array}

Question 8:

\begin{array}{l} Calculate the value of (8.4 - 2.64) \div \frac{4}{3} and express the answer correct \\ to two decimal places . \end{array}

Solution:

\begin{array}{l} (8.4 - 2.64) \div \frac{4}{3} \\ = {5.76}^{1.44} \times \frac{3}{4} \\ = 4.32 \end{array}

4.2.1 Decimals, PT3 Practice

Posted on February 20, 2017 by user

Question 1:
62.4 – 36.02 + 12.6 =

Solution:

Question 2:
4.76 × 7.2 ÷ 0.3 =

Solution:

\begin{array}{l} 4.76 \times 7.2 \div 0.3 \\ = 34.272 \div 0.3 \\ = \frac{34.272}{0.3} \\ = \frac{34.272 \times 10}{0.3 \times 10} \\ = \frac{342.72}{3} \\ = 114.24 \end{array}

Question 3:
0.12 × (5.9 – 1.33) ÷ 0.8 =

Solution:

\begin{array}{l} 0.12 \times (5.9 - 1.33) \div 0.8 \\ = 0.12 \times 4.57 \div 0.8 \\ = 0.5484 \div 0.8 \\ = \frac{0.5484}{0.8} \\ = \frac{0.5484 \times 10}{0.8 \times 10} \\ = \frac{5.484}{8} \\ = 0.6855 \end{array}

Question 4:
14.83 + (20.04 – 10.68) ÷ 1.8 =

Solution:

\begin{array}{l} 14.83 + (20.04 - 10.68) \div 1.8 \\ = 14.83 + 9.36 \div 1.8 \\ = 14.83 + \frac{9.36 \times 10}{1.8 \times 10} \\ = 14.83 + \frac{93.6}{18} \\ = 14.83 + 5.2 \\ = 20.03 \end{array}

3.2.3 Fractions, PT3 Practice

Posted on February 9, 2017 by user

Question 11:
Table below shows the types of fruit tree planted by Azmi in his orchard.

(a) Calculate the number of guava trees.
(b) 100 mangosteen trees died due to fungus.
Find the total number of the remaining trees.

Solution:
(a)

\begin{array}{l} Number of Guava trees \\ = \frac{1}{3} \times 180 \\ = 60 \end{array}

(b)

\begin{array}{l} Number of mangosteen and guava trees \\ = 180 + 60 \\ = 240 \\ Fraction of mangosteen and guava trees = \frac{3}{5} \\ Total number of trees \\ = \frac{5}{3} \times 240 \\ = 400 \\ Total number of remaining trees \\ = 400 - 100 \\ = 300 \end{array}

Question 12:
A palm oil processing factory has a number of workers.

\frac{4}{7}

of the workers are skilled workers. If

\frac{3}{5}

of the general workers are 18 females, find the total number of workers in the factory.

Solution:

\begin{array}{l} \frac{3}{5} of the general workers are 18 females . \\ Let the number of general workers = w \\ \frac{3}{5} \times w = 18 \\ w = 18 \times \frac{5}{3} \\ = 30 \\ Hence the total number of workers in the factory \\ = 30 \div (\frac{7}{7} - \frac{4}{7}) \\ = 30 \div \frac{3}{7} \\ = 30 \times \frac{7}{3} \\ = 70 \end{array}

Question 13:
In a fruit basket,

\frac{2}{5}

are mangoes and the rest are kiwis.
If

\frac{2}{3}

of the mangoes or 12 of them are in good condition, calculate the number of kiwis in the basket.

Solution:

\begin{array}{l} Let the number of mangos \\ in the basket = x \\ \frac{2}{3} \times x = 12 \\ x = 12 \times \frac{3}{2} \\ x = 18 mangoes \\ Total number of mangoes and \\ kiwis in the basket \\ = 18 \times \frac{5}{2} \\ = 45 \\ Hence, the number of kiwis \\ in the basket \\ = (1 - \frac{2}{5}) \times 45 \\ = (\frac{5}{5} - \frac{2}{5}) \times 45 \\ = \frac{3}{5} \times 45 \\ = 27 \end{array}

3.2.2 Fractions, PT3 Practice

Posted on February 7, 2017 by user

Question 6:

1 \frac{1}{2} \div \frac{1}{4} \times \frac{4}{5} =

Solution:

\begin{array}{l} 1 \frac{1}{2} \div \frac{1}{4} \times \frac{4}{5} \\ = \frac{3}{2} \times \frac{4^{2}}{1} \times \frac{4}{5} \\ = \frac{24}{5} \\ = 4 \frac{4}{5} \end{array}

Question 7:

4 \frac{1}{5} \div 1 \frac{1}{6} \times 2 \frac{2}{9} =

Solution:

\begin{array}{l} 4 \frac{1}{5} \div 1 \frac{1}{6} \times 2 \frac{2}{9} \\ = \frac{21^{3}}{5} \times \frac{6^{2}}{7} \times \frac{20^{4}}{9^{3}} \\ = 8 \end{array}

Question 8:

2 \frac{3}{4} \times 1 \frac{1}{3} \div 7 \frac{1}{3} =

Solution:

\begin{array}{l} 2 \frac{3}{4} \times 1 \frac{1}{3} \div 7 \frac{1}{3} \\ = \frac{11}{4} \times \frac{4}{3} \div \frac{22}{3} \\ = \frac{11}{4} \times \frac{4}{3} \times \frac{3}{22^{2}} \\ = \frac{1}{2} \end{array}

Question 9:

4 \frac{5}{6} - 2 \frac{1}{3} \div \frac{5}{9} =

Solution:

\begin{array}{l} 4 \frac{5}{6} - 2 \frac{1}{3} \div \frac{5}{9} \\ = 4 \frac{5}{6} - (\frac{7}{3} \div \frac{5}{9}) \\ = 4 \frac{5}{6} - (\frac{7}{3} \times \frac{9^{3}}{5}) \\ = 4 \frac{5}{6} - \frac{21}{5} \\ = 4 \frac{5}{6} - 4 \frac{1}{5} \\ = \frac{25}{30} - \frac{6}{30} \\ = \frac{19}{30} \end{array}

Question 10:

(\frac{7}{9} + \frac{11}{15}) \div (7 \frac{8}{15} - 4 \frac{1}{5}) =

Solution:

\begin{array}{l} (\frac{7}{9} + \frac{11}{15}) \div (4 \frac{8}{15} - 3 \frac{1}{5}) \\ = (\frac{35}{45} + \frac{33}{45}) \div (4 \frac{8}{15} - 3 \frac{3}{15}) \\ = \frac{68}{45} \div 1 \frac{5}{15} \\ = \frac{68}{45} \div 1 \frac{1}{3} \\ = \frac{68}{45} \div \frac{4}{3} \\ = \frac{68^{17}}{45^{15}} \times \frac{3}{4} \\ = \frac{17}{15} \\ = 1 \frac{2}{15} \end{array}

3.2.1 Fractions, PT3 Practice

Posted on February 5, 2017 by user

Question 1:

3 \frac{2}{5} + 1 \frac{5}{6} - \frac{1}{5} =

Solution:

\begin{array}{l} 3 \frac{2}{5} + 1 \frac{5}{6} - \frac{1}{5} \\ = 3 \frac{12}{30} + 1 \frac{25}{30} - \frac{6}{30} \\ = 4 \frac{37}{30} - \frac{6}{30} \\ = 4 \frac{31}{30} \\ = 5 \frac{1}{30} \end{array}

Question 2:

6 \frac{1}{12} - 3 \frac{2}{3} - 1 \frac{5}{6} =

Solution:

\begin{array}{l} 6 \frac{1}{12} - 3 \frac{2}{3} - 1 \frac{5}{6} \\ = 6 \frac{1}{12} - 3 \frac{8}{12} - 1 \frac{10}{12} \\ = (5 \frac{13}{12} - 3 \frac{8}{12}) - 1 \frac{10}{12} \\ = 2 \frac{5}{12} - 1 \frac{10}{12} \\ = 1 \frac{17}{12} - 1 \frac{10}{12} \\ = \frac{7}{12} \end{array}

Question 3:

30 - (\frac{2}{7} \div \frac{2}{21}) =

Solution:

\begin{array}{l} 30 - (\frac{2}{7} \div \frac{2}{21}) \\ = 30 - (\frac{2}{7} \times \frac{21^{3}}{2}) \\ = 30 - 3 \\ = 27 \end{array}

Question 4:

(7 \frac{1}{2} - 3 \frac{2}{3}) \times \frac{12}{69} =

Solution:

\begin{array}{l} (7 \frac{1}{2} - 3 \frac{2}{3}) \times \frac{12}{69} \\ = (7 \frac{3}{6} - 3 \frac{4}{6}) \times \frac{12}{69} \\ = (6 \frac{9}{6} - 3 \frac{4}{6}) \times \frac{12}{69} \\ = 3 \frac{5}{6} \times \frac{12}{69} \\ = \frac{23}{6} \times \frac{12^{2}}{69^{3}} \\ = \frac{2}{3} \end{array}

Question 5:

1 \frac{1}{5} \div (4 - 2 \frac{1}{2}) =

Solution:

\begin{array}{l} 1 \frac{1}{5} \div (4 - 2 \frac{1}{2}) \\ = 1 \frac{1}{5} \div (3 \frac{2}{2} - 2 \frac{1}{2}) \\ = \frac{6}{5} \div (1 \frac{1}{2}) \\ = \frac{6}{5} \div \frac{3}{2} \\ = \frac{6^{2}}{5} \times \frac{2}{3} \\ = \frac{4}{5} \end{array}

2.2.4 Number Patterns and Sequences, PT3 Practice

Posted on January 25, 2017 by user

[adinserter block="3"]

Question 16:
State the first two common multiples of 3, 5 and 6.

Solution:
Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, …
Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, …
Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …

The first two common multiples of 3, 5 and 6 are 30 and 60.

[adinserter block="3"]

Question 17:
Find the lowest common multiple (LCM) of 4, 8 and 24.

Solution:

[adinserter block="3"]

Question 18:
Find the lowest common multiple (LCM) of 8, 12 and 15.

Solution:

[adinserter block="3"]

Question 19:
Find the highest common factor (HCF) of 26, 52 and 156.

Solution:

[adinserter block="3"]

Question 20:
Given that (m + 5) is the highest common factor of 81 and 108, find the value of m.

Solution:

2.2.3 Number Patterns and Sequences, PT3 Practice

Posted on January 22, 2017 by user

[adinserter block="3"]

Question 11:
State all the prime factors of 156.

Solution:

\begin{array}{l} Factors of 156 : \\ 1 \times 156 \\ 2 \times 78 \\ 3 \times 52 \\ 4 \times 39 \\ 6 \times 26 \\ 12 \times 13 \\ 2, 3 and 13 are the prime factors of 156. \end{array}

[adinserter block="3"]

Question 12:
State all the prime factors of 182.

Solution:

\begin{array}{l} Factors of 182 : \\ 1 \times 182 \\ 2 \times 91 \\ 7 \times 26 \\ 13 \times 14 \\ 2, 7, 13 and 91 are the prime factors of 182. \end{array}

4.9.5 Sexual Reproduction in Flowering Plants (Structured Question 1 & 2)

Posted on January 8, 2017 by user

Question 1:
Diagram below shows a longitudinal section of the reproductive parts of a flower during fertilization.

(a) On the Diagram, name the structures J, K, L and M.

(b)(i) In the space below, draw a section through the ovule, showing all the cells in M.
(b)(ii) What is the significance of having two K structures in the fertilization?

(c) In the Diagram, the structure Y has to be kept dormant for future research purposes.
(i) Explain how Y can be prevented from germinating.
(ii) If Y is to be germinated, suggest one method to stimulate the germination of Y.

Answer:
(a)
J : Pollen tube
K : Male gamete
L : Ovary
M : Embryo sac

(b)(i)

(b)(ii)
- One K/ male gamete fertilizes an egg cell to form a diploid zygote.
- One more K fuses with two polar nuclei to form a triploid zygote.

(c)(i)
- Keep Y in a dry place
- Moisture initiates germination

(c)(ii)
Spraying a sugary solution onto Y