Question 1:
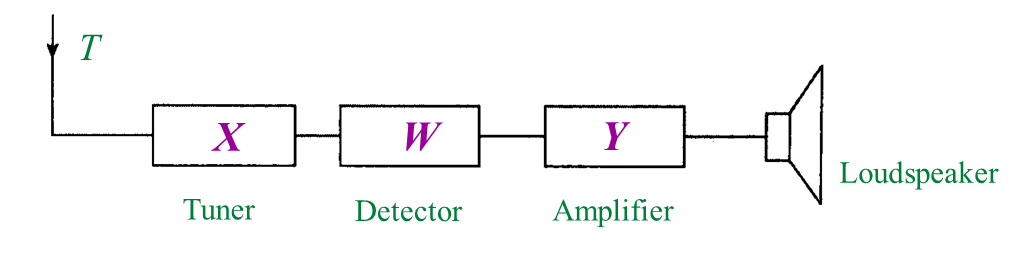
Diagram 1.1 shows three types of electronic components used in a radio receiver.
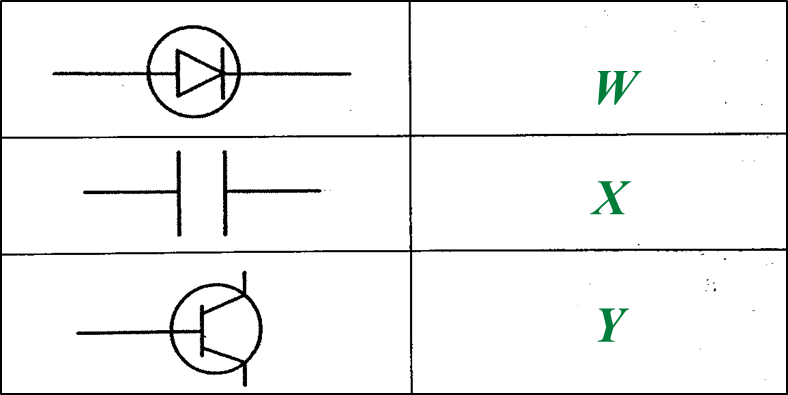 Diagram 1.1
Diagram 1.1
(a) Name electronic components W and Y. [2 marks]
(b) State the function of electronic component X. [1 mark]
(c) Diagram 1.2 shows a black diagram of a radio receiver.
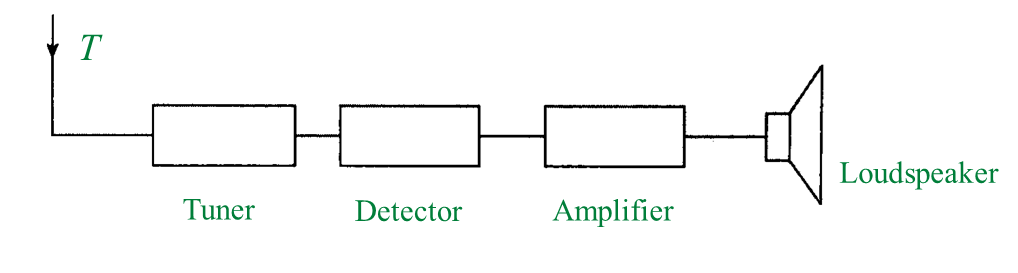 Diagram 1.2
Diagram 1.2
(i) Write any two electronic components, W, X or Y from Diagram 1.1 into the corresponding blocks provided in Diagram 1.2. [2 marks]
(ii) What type of wave is received by T?
Mark (\/) your answer in the box provided in Diagram 1.3. [1 mark]
 Diagram 1.3
Diagram 1.3
Answer:
(a)
W: Diode
Y: Transistor
(b)
(c)(i)
 (c)(ii)
(c)(ii)

Diagram 1.1 shows three types of electronic components used in a radio receiver.
 Diagram 1.1
Diagram 1.1(a) Name electronic components W and Y. [2 marks]
(b) State the function of electronic component X. [1 mark]
(c) Diagram 1.2 shows a black diagram of a radio receiver.
 Diagram 1.2
Diagram 1.2(i) Write any two electronic components, W, X or Y from Diagram 1.1 into the corresponding blocks provided in Diagram 1.2. [2 marks]
(ii) What type of wave is received by T?
Mark (\/) your answer in the box provided in Diagram 1.3. [1 mark]
 Diagram 1.3
Diagram 1.3Answer:
(a)
W: Diode
Y: Transistor
(b)
- Stores electric charges and discharges them at regular intervals when required
- To channel the flow of radio frequency carrier waves into the Earth.
- When connected in parallel with the inductor, it determines the frequency of the radio wave that will be detected.
(any one)
(c)(i)
 (c)(ii)
(c)(ii)
Question 2:
Table 1 shows the symbols of electronic components.
(a) Complete Table 1 using the name of electronic components given. [3 marks]
 Table 1
Table 1
Diagram 2 shows a block diagram of a radio receiver system.
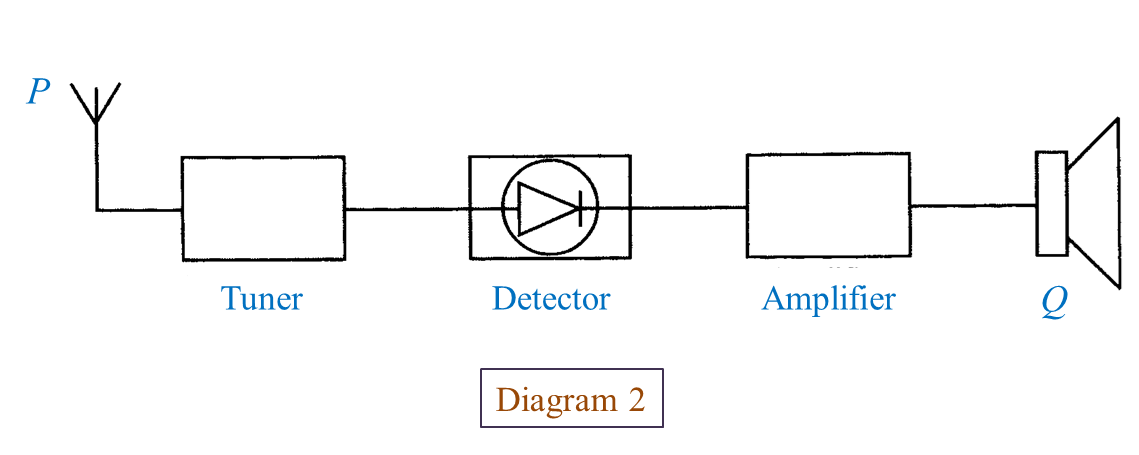 (b) What is the function of P? [1 mark]
(b) What is the function of P? [1 mark]
(c) What is Q? [1 mark]
(d) State the energy change that occurs at Q? [1 mark]
Answer:
(a)
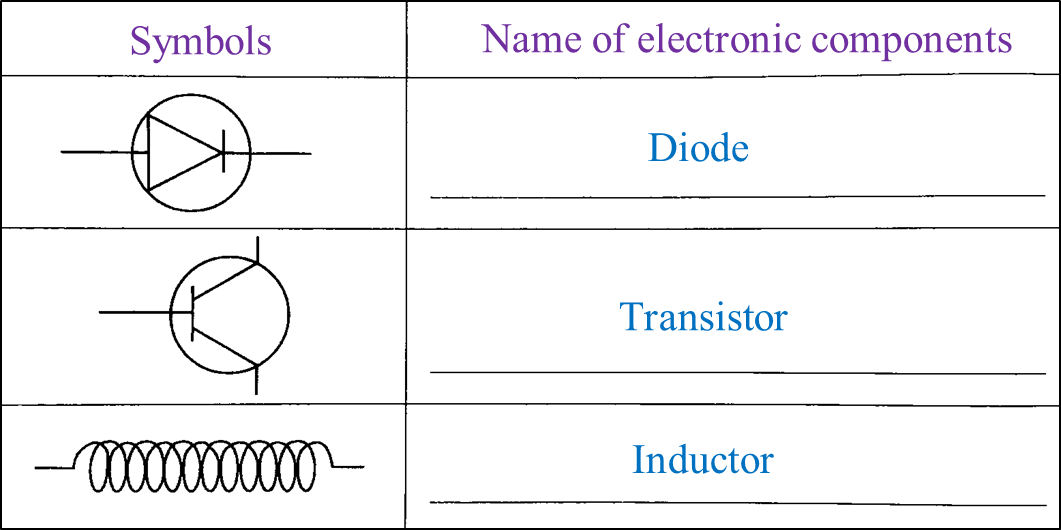
Table 1 shows the symbols of electronic components.
(a) Complete Table 1 using the name of electronic components given. [3 marks]

 Table 1
Table 1Diagram 2 shows a block diagram of a radio receiver system.
 (b) What is the function of P? [1 mark]
(b) What is the function of P? [1 mark](c) What is Q? [1 mark]
(d) State the energy change that occurs at Q? [1 mark]
Answer:
(a)

(b) Receives modulated radio waves from stations.
(c)(i) Loudspeaker
(c)(ii) Electrical energy → sound energy
 Diagram 1
Diagram 1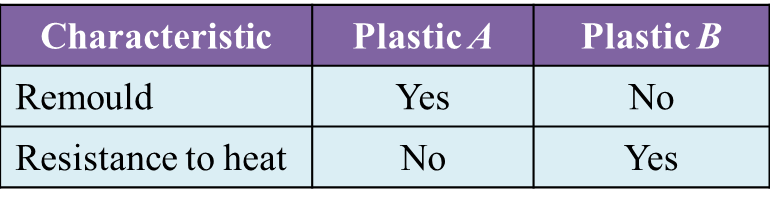 Table 1
Table 1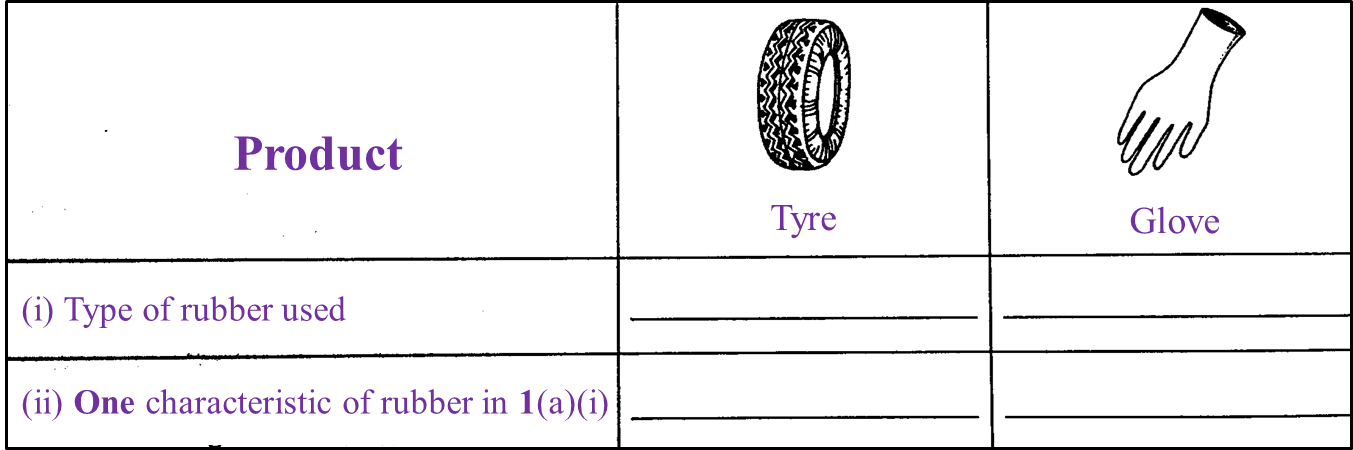 Table 1.1
Table 1.1 Table 1.2
Table 1.2

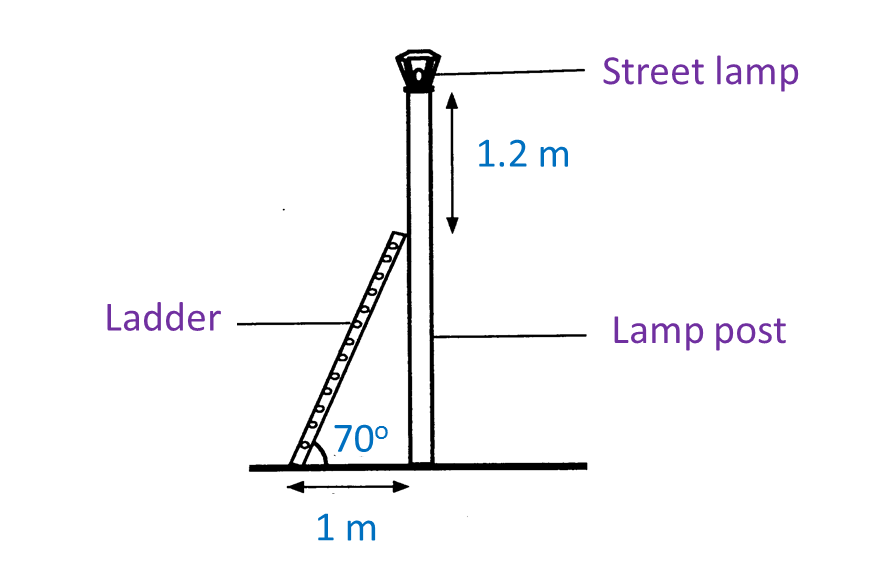 (a) What is the length, in m, of the ladder?
(a) What is the length, in m, of the ladder?
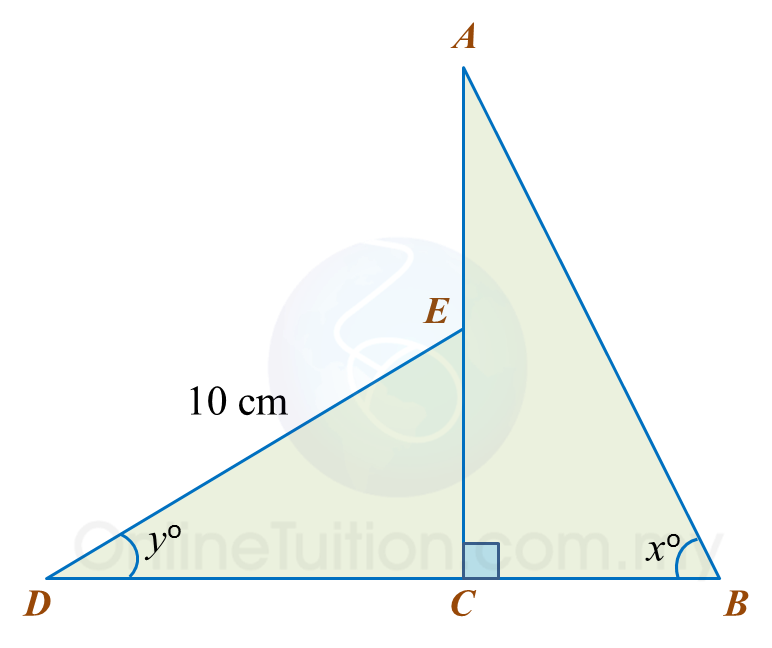

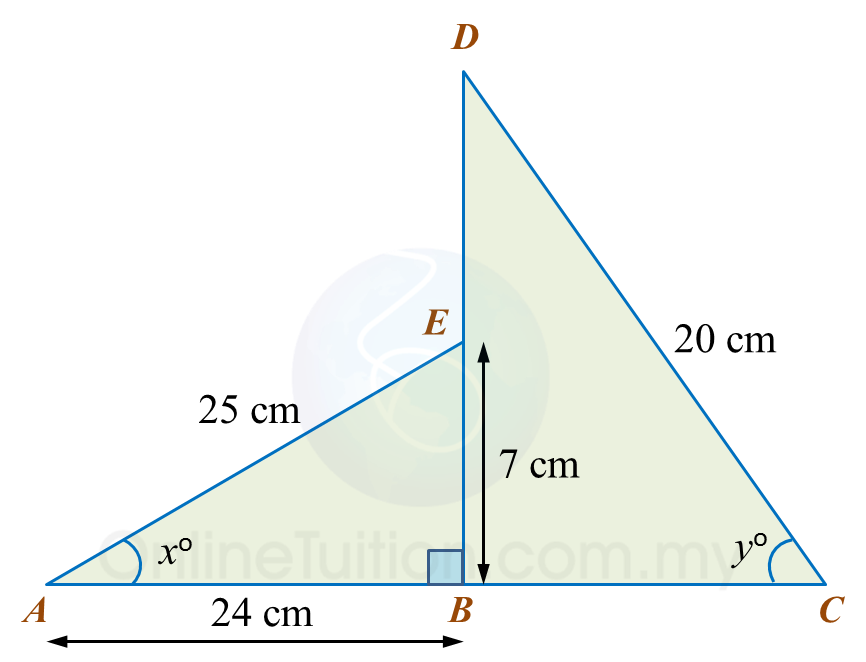
 Calculate
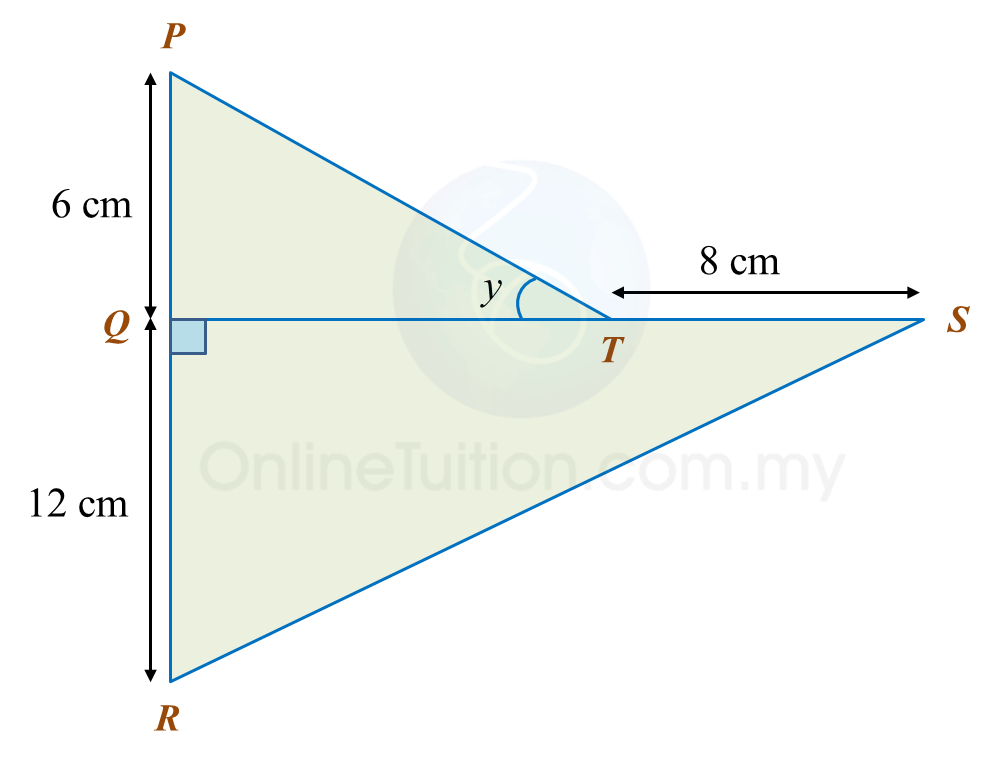
Calculate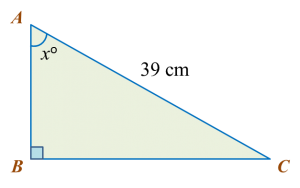
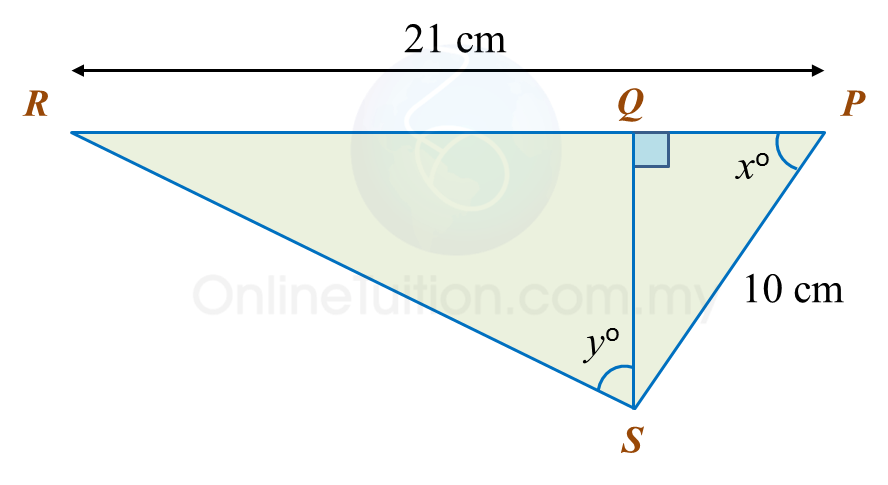





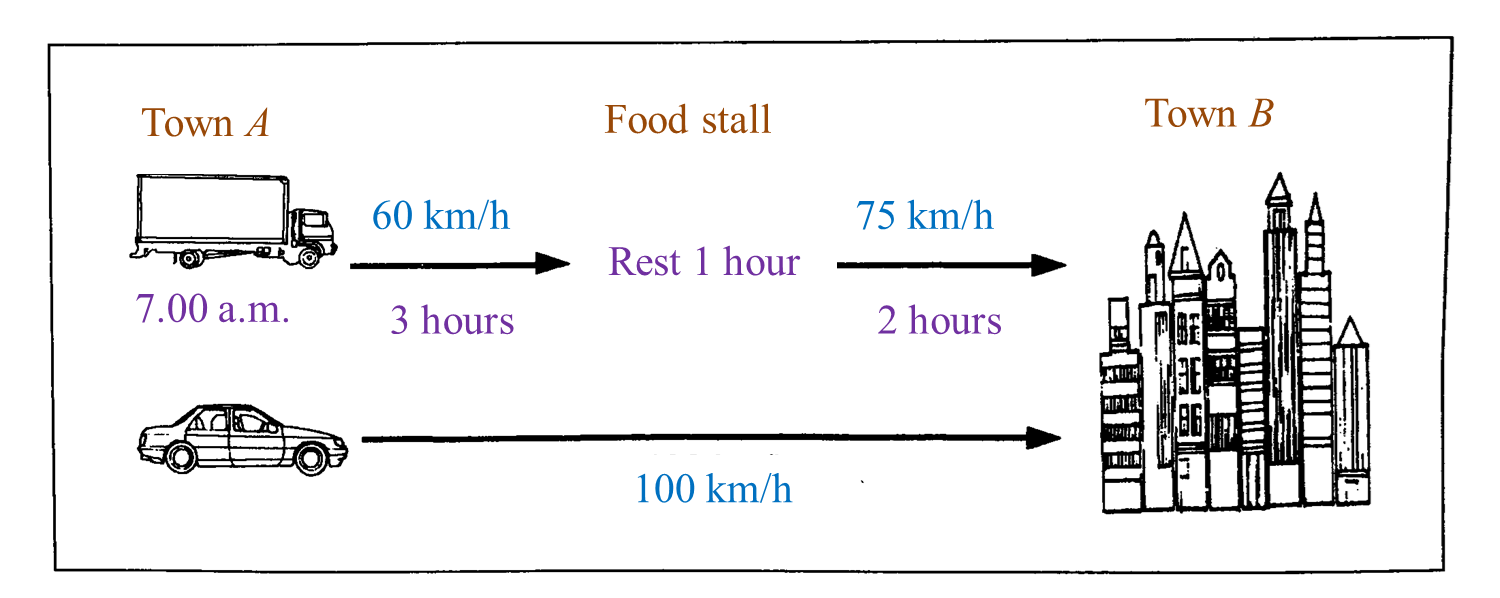
 (a) Rahim rode his bicycle from Town P at 9.00 a.m. and took 2 hours to reach Town Q.
(a) Rahim rode his bicycle from Town P at 9.00 a.m. and took 2 hours to reach Town Q.