Question 1:
Diagram 1.1 and Diagram 1.2 show an experiment to study the collision between trolleys of different masses with a plasticine block.
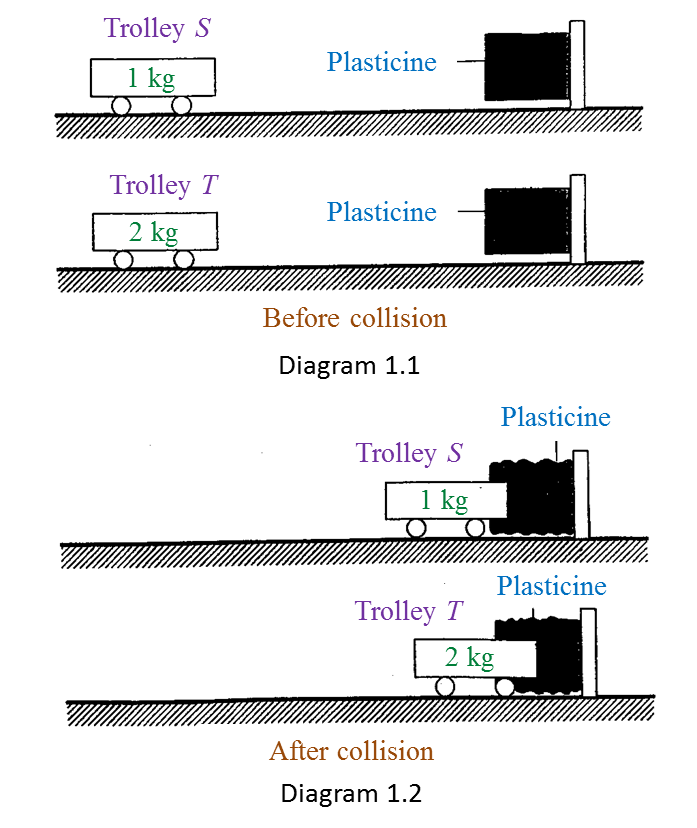
Both trolleys move with the same velocity.
(a) State the variables in this experiment.
(i) Manipulated variable [1 mark]
(ii) Responding variable [1 mark]
(b)(i) What can you observe about the plasticine block after the collision? [1 mark]
(ii) State one inference that can be made based on the observation in (b)(i). [1 mark]
(c) State the hypothesis of this experiment. [1 mark]
Answer:
(a)(i) Mass of the trolley
(a)(ii) Depth of the dent on the plasticine block
(b)(i)
Trolley T produced a deeper dent on the plasticine block compared to the dent produced by trolley S after their collision with the plasticine block.
(b)(ii)
When a moving trolley with a bigger mass collides with a plasticine block, it produces a deeper dent on the plasticine block.
(c) The bigger the mass of a moving trolley which collides with a plasticine block, the deeper the dent which will be formed on the plasticine block.
Diagram 1.1 and Diagram 1.2 show an experiment to study the collision between trolleys of different masses with a plasticine block.

Both trolleys move with the same velocity.
(a) State the variables in this experiment.
(i) Manipulated variable [1 mark]
(ii) Responding variable [1 mark]
(b)(i) What can you observe about the plasticine block after the collision? [1 mark]
(ii) State one inference that can be made based on the observation in (b)(i). [1 mark]
(c) State the hypothesis of this experiment. [1 mark]
Answer:
(a)(i) Mass of the trolley
(a)(ii) Depth of the dent on the plasticine block
(b)(i)
Trolley T produced a deeper dent on the plasticine block compared to the dent produced by trolley S after their collision with the plasticine block.
(b)(ii)
When a moving trolley with a bigger mass collides with a plasticine block, it produces a deeper dent on the plasticine block.
(c) The bigger the mass of a moving trolley which collides with a plasticine block, the deeper the dent which will be formed on the plasticine block.
Question 2:
Diagram 2.1 shows an experiment to study the collision of a trolley with block M. After collision, block M is displaced to a new position.
The experiment is repeated using two trolleys as shown in Diagram 2.2.
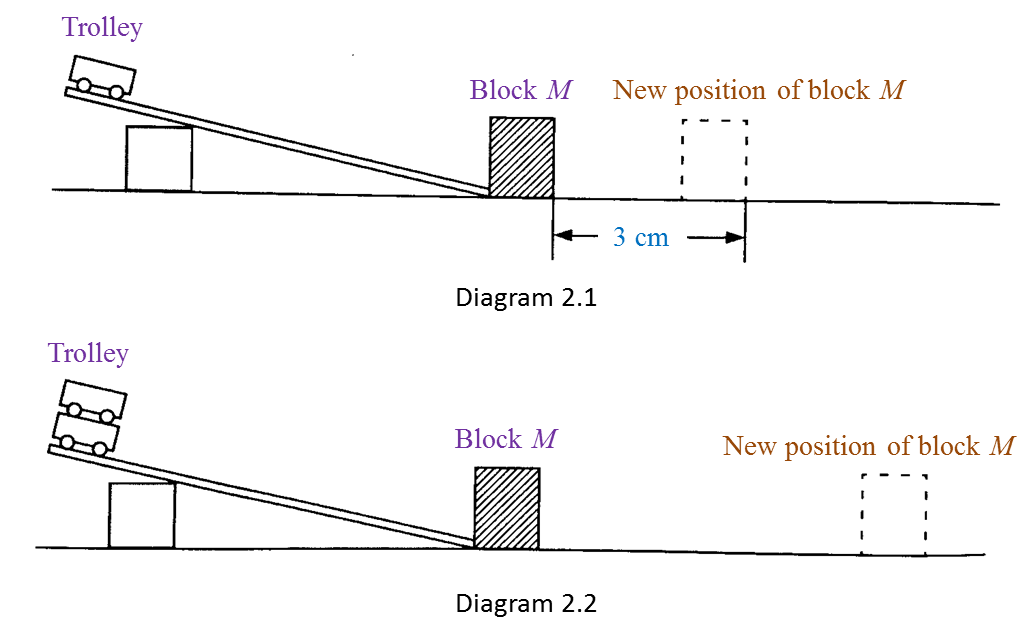
The result of this experiment is shown in Table below.
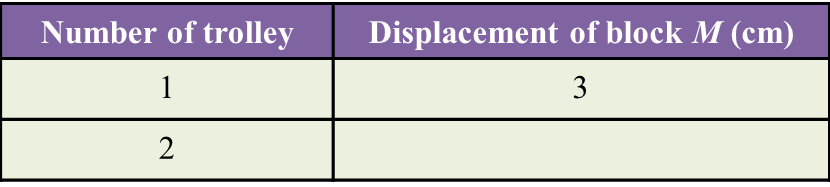
(a) Measure the displacement of block M after the collision in Diagram 2.2. [1 mark]
(b) State one observation about displacement of block M in diagram 2.1 and 2.2. [1 mark]
(c) State the variables in this experiment.
(i) Constant variable [1 mark]
(ii) Manipulated variable [1 mark]
(d) Predict the displacement of block M if three trolleys are used. [1 mark]
Answer:
(a) 6 cm
(b) The displacement of block M increases when the number of trolley increases.
(c)(i) Length and slope of runway, mass of block M.
(c)(ii) The number of trolley used
(d) 9 cm
Diagram 2.1 shows an experiment to study the collision of a trolley with block M. After collision, block M is displaced to a new position.
The experiment is repeated using two trolleys as shown in Diagram 2.2.

The result of this experiment is shown in Table below.

(a) Measure the displacement of block M after the collision in Diagram 2.2. [1 mark]
(b) State one observation about displacement of block M in diagram 2.1 and 2.2. [1 mark]
(c) State the variables in this experiment.
(i) Constant variable [1 mark]
(ii) Manipulated variable [1 mark]
(d) Predict the displacement of block M if three trolleys are used. [1 mark]
Answer:
(a) 6 cm
(b) The displacement of block M increases when the number of trolley increases.
(c)(i) Length and slope of runway, mass of block M.
(c)(ii) The number of trolley used
(d) 9 cm