15.2.1 Trigonometry, PT3 Focus Practice

15.2.1 Trigonometry, PT3 Focus Practice

Question 1:

Diagram below shows a right-angled triangle ABC.

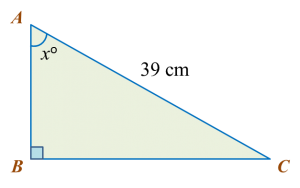
It is given that

\cos x^{o} = \frac{5}{13}

, calculate the length, in cm, of AB.

Solution:

\begin{array}{l} \cos x^{o} = \frac{A B}{A C} \\ \cos x^{o} = \frac{5}{13} \\ \frac{A B}{39} = \frac{5}{13} \\ A B = \frac{5}{13} \times 39 \\ = 15 cm \end{array}

Question 2:

In the diagram, PQR and QTS are straight lines.

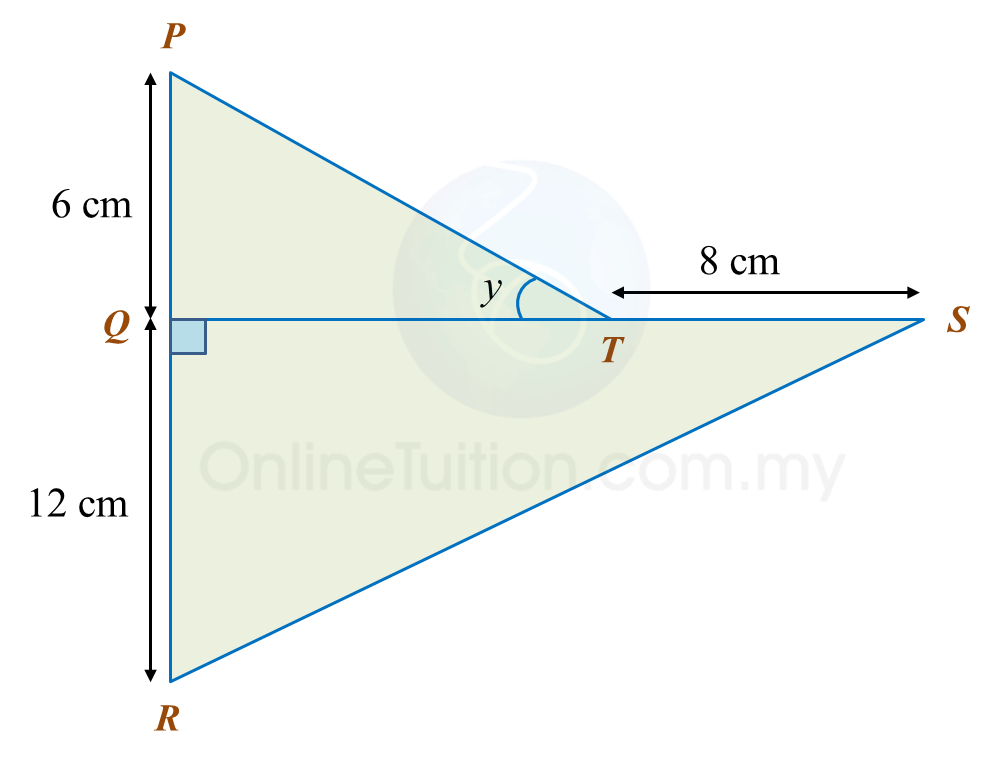
It is given that

\tan y = \frac{3}{4}

, calculate the length, in cm, of RS.

Solution:

\begin{array}{l} In △ P Q T, \\ \tan y = \frac{P Q}{Q T} \\ \frac{3}{4} = \frac{6}{Q T} \\ Q T = 6 \times \frac{4}{3} \\ = 8 cm \\ In △ Q R S, Q S = 8 + 8 = 16 cm \\ ∴ R S^{2} = 12^{2} + 16^{2} \leftarrow pythagoras' Theorem \\ = 144 + 256 \\ = 400 \\ R S = \sqrt{400} \\ = 20 cm \end{array}

Question 3:

In the diagram, PQR is a straight line.

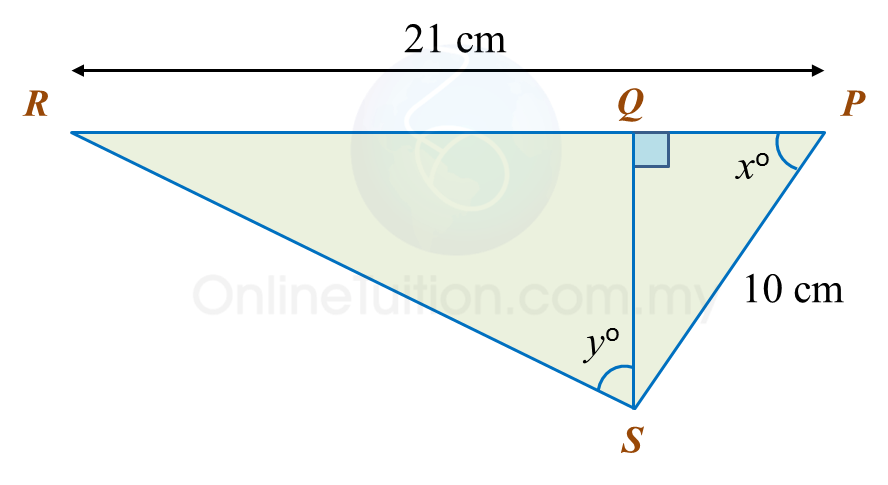
It is given that

\cos x^{o} = \frac{3}{5}

, hence sin y^o =

Solution:

\begin{array}{l} \cos x^{o} = \frac{P Q}{P S} \\ \frac{P Q}{10} = \frac{3}{5} \\ P Q = \frac{3}{5} \times 10 \\ = 6 cm \\ Q R = P R - P Q \\ = 21 - 6 \\ = 15 cm \end{array}

\begin{array}{l} Q S^{2} = 10^{2} - 6^{2} \leftarrow pythagoras' Theorem \\ = 100 - 36 \\ = 64 \\ Q S = \sqrt{64} \\ = 8 cm \\ R S^{2} = 15^{2} + 8^{2} \\ = 225 + 64 \\ = 289 \\ R S = \sqrt{289} \\ = 17 cm \\ \sin y^{o} = \frac{15}{17} \end{array}

Question 4:

Diagram below consists of two right-angled triangles.

Determine the value of cos x^o.

Solution:

\begin{array}{l} A C = \sqrt{13^{2} - 12^{2}} \\ = \sqrt{25} \\ = 5 cm \\ C D = \sqrt{5^{2} - 3^{2}} \\ = \sqrt{16} \\ = 4 cm \\ \cos x^{o} = \frac{C D}{A C} \\ = \frac{4}{5} \end{array}

Question 5:

Diagram below consists of two right-angled triangles ABE and DBC.

ABC and EBD are straight lines.

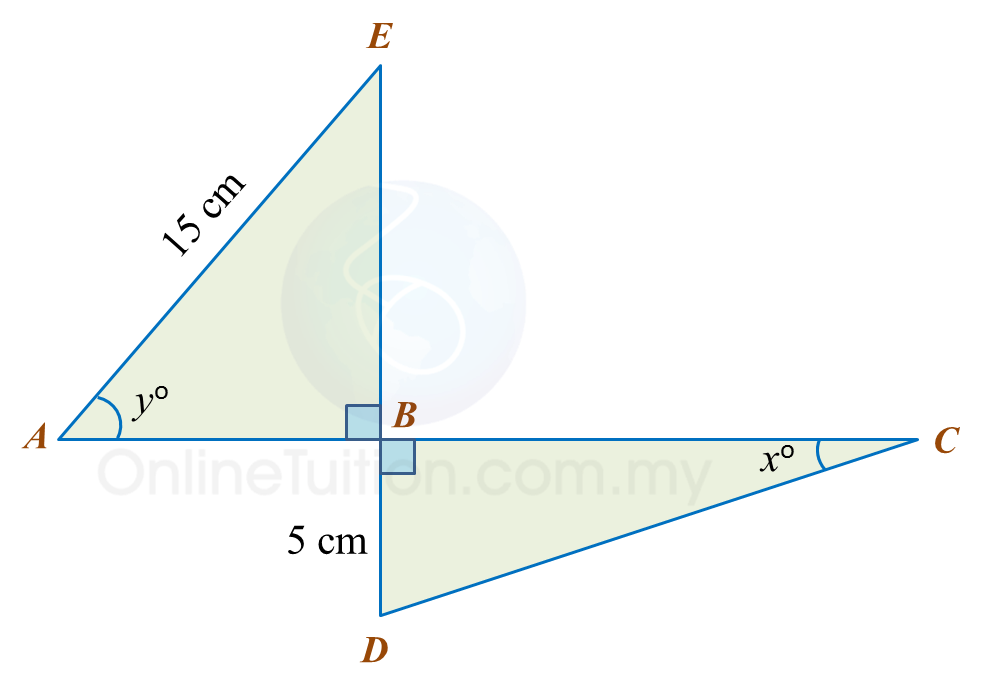
It is given that

s i n x^{o} = \frac{5}{13} and \cos y^{o} = \frac{3}{5} .

(a) Find the value of tan x^o.

(b) Calculate the length, in cm, of ABC.

Solution:

(a)

\begin{array}{l} s i n x^{o} = \frac{5}{13}, D C = 13 cm \\ B C = \sqrt{13^{2} - 5^{2}} \\ = \sqrt{144} \\ = 12 cm \\ Thus, \tan x^{o} = \frac{5}{12} \end{array}

(b)

\begin{array}{l} \cos y^{o} = \frac{A B}{15} \\ \frac{3}{5} = \frac{A B}{15} \\ A B = 9 cm \\ Thus, A B C = 9 + 12 \\ = 21 cm \end{array}