Question 6:
In diagram below, AEC and BCD are straight lines. E is the midpoint of AC.
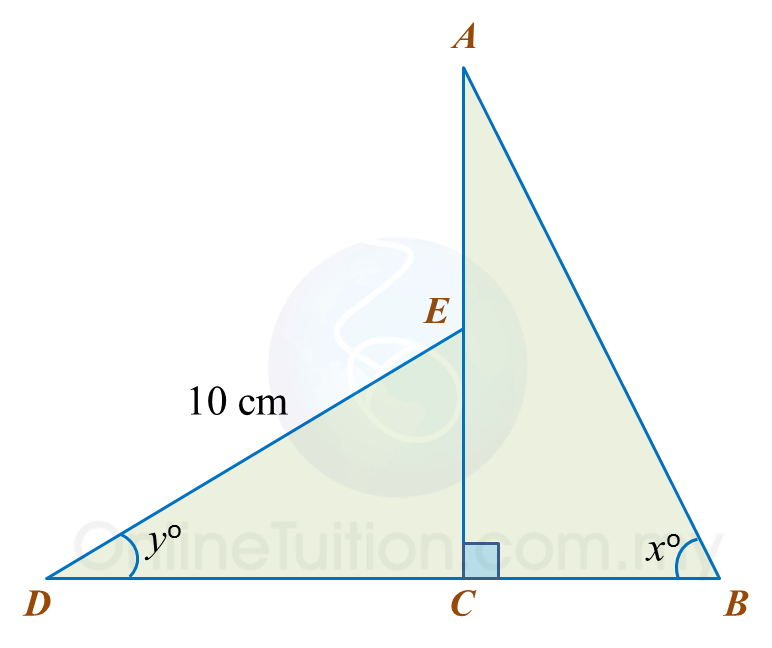
Given cosx=513 and siny=35
(a) find the value of tan x.
(b) Calculate the length, in cm, of BD.
Solution:
(a)Given cos x=513, therefore BC=5, AB=13AC=√132−52 =√169−25 =√144 =12 cmtan x=ACBC=125
(b)For ΔDCE:siny=35ECDE=35EC10=35EC=35×10=6 cmDC2=102−62 =64 DC=8 cmFor ΔABC:AC=2×6=12 cmtanx=12512CB=125CB=5 cmBD=DC+CB=8 cm + 5 cm=13 cm
In diagram below, AEC and BCD are straight lines. E is the midpoint of AC.

Given cosx=513 and siny=35
(a) find the value of tan x.
(b) Calculate the length, in cm, of BD.
Solution:
(a)Given cos x=513, therefore BC=5, AB=13AC=√132−52 =√169−25 =√144 =12 cmtan x=ACBC=125
(b)For ΔDCE:siny=35ECDE=35EC10=35EC=35×10=6 cmDC2=102−62 =64 DC=8 cmFor ΔABC:AC=2×6=12 cmtanx=12512CB=125CB=5 cmBD=DC+CB=8 cm + 5 cm=13 cm
Question 7:
In diagram below, T is the midpoint of the line PR.

(a) Find the value of tan xo.
(b) Calculate the length, in cm, of PQ.
Solution:
(a)TR2=132−122 =169−144 =25TR=√25 =5 cmtanxo=125
(b)PR=2×5 cm =10 cmPQ2=102−82 =100−64 =36PQ=√36 =6 cm
In diagram below, T is the midpoint of the line PR.

(a) Find the value of tan xo.
(b) Calculate the length, in cm, of PQ.
Solution:
(a)TR2=132−122 =169−144 =25TR=√25 =5 cmtanxo=125
(b)PR=2×5 cm =10 cmPQ2=102−82 =100−64 =36PQ=√36 =6 cm
Question 8:
In diagram below, ABE and DBC are two right-angled triangles ABC and DEB are straight lines.
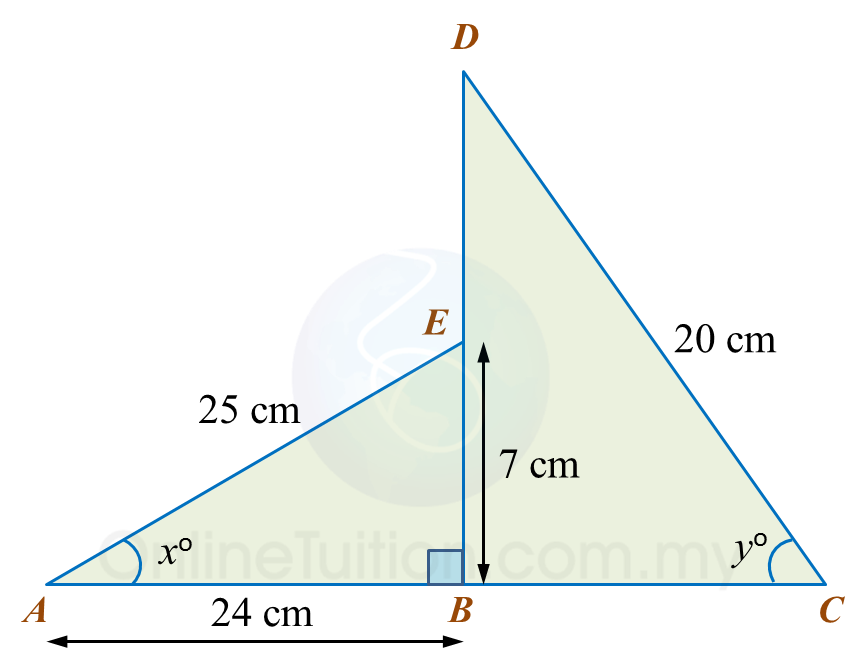
It is given that cosyo=35.
(a) Find the value of tan xo.
(b) Calculate the length, in cm, of DE.
Solution:
(a) tanxo=724
(b)cosyo=BC20 35=BC20BC=35×20 =12 cm∴
In diagram below, ABE and DBC are two right-angled triangles ABC and DEB are straight lines.

It is given that cosyo=35.
(a) Find the value of tan xo.
(b) Calculate the length, in cm, of DE.
Solution:
(a) tanxo=724
(b)cosyo=BC20 35=BC20BC=35×20 =12 cm∴
Question 9:
Diagram below shows a vertical pole, PQ. At 2.30 p.m. and 5.00 p.m., the shadow of the pole falls on QR and QS respectively.
 Calculate
Calculate
(a) the height, in m, of the pole.
(b) the value of w.
Solution:
(a)
(b)
Diagram below shows a vertical pole, PQ. At 2.30 p.m. and 5.00 p.m., the shadow of the pole falls on QR and QS respectively.
 Calculate
Calculate(a) the height, in m, of the pole.
(b) the value of w.
Solution:
(a)
(b)