11.2.1 Linear Equations II, PT3 Focus Practice
Question 1:
It is given that 2x = 6 and 3x + y = 10.
Calculate the value of y.
Solution:
2x = 6
x = 3
Substitute x = 3 into 3x + y = 10
3 (3) + y = 10
y = 10 – 9
y = 1
Question 2:
It is given that y = –1 and x – 3y = –10.
Calculate the value of x.
Solution:
Substitute y = –1 into x – 3y = –10
x – 3 (–1) = –10
x + 3 = –10
x = –10 – 3
x = –13
Question 3:
It is given that 7x – 2y = 19 and x + y = 13.
Calculate the value of y.
Solution:
Using Substitution method
7x – 2y = 19 -------- (1)
x + y = 13 ------- (2)
From equation (2),
x = 13 – y ------- (3)
Substitute equation (3) into equation (1),
7x – 2y = 19
7 (13 – y) – 2y = 19
91 – 7y – 2y = 19
– 9y = 19 – 91
– 9y = –72
y = 8
Question 4:
It is given that 2x – y = 5 and 3x – 2y = 8.
Calculate the value of x.
Solution:
Using Elimination method
2x – y = 5 -------- (1)
3x – 2y = 8 ------- (2)
(1) × 2: 4x – 2y = 10 -------- (3)
3x – 2y = 8 ------- (2)
(3) – (2): x – 0 = 2
x = 2
Question 5:
It is given that x + 2y = 4 and x + 6y = –4.
Calculate the value of x.
Solution:
Using Elimination method
x + 2y = 4 -------- (1)
x + 6y = –4 ------- (2)
(1) × 3: 3x + 6y = 12 -------- (3)
x + 6y = –4 ------- (2)
(3) – (2): 2x = 12 – (–4)
2x = 16
x = 8
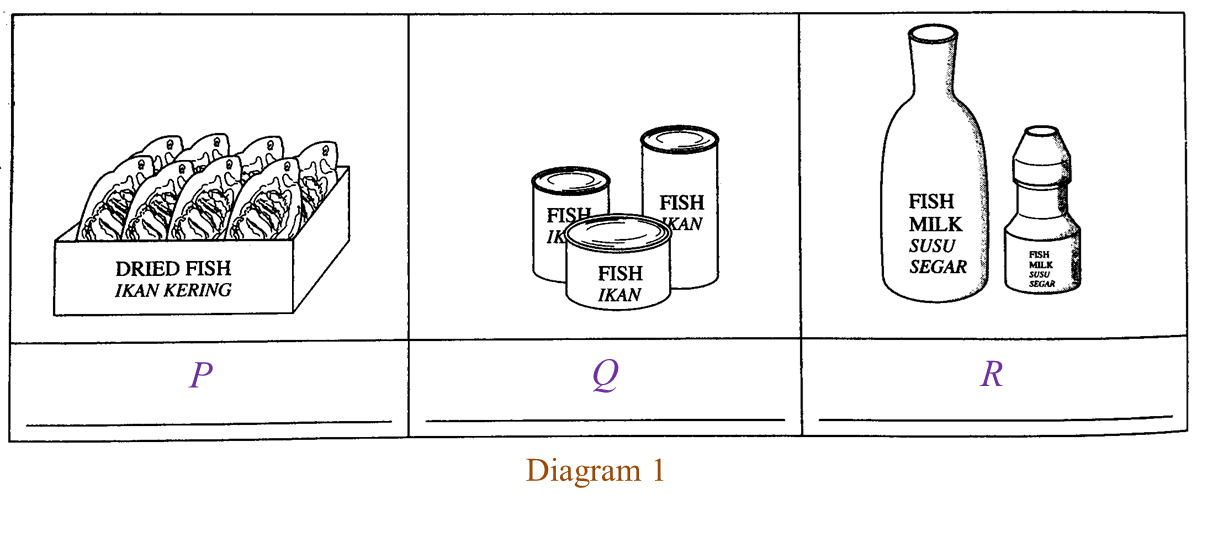
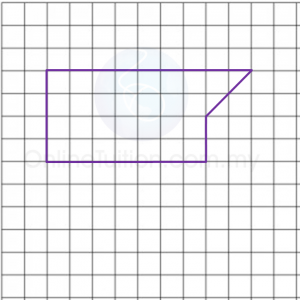
 Diagram 2.1
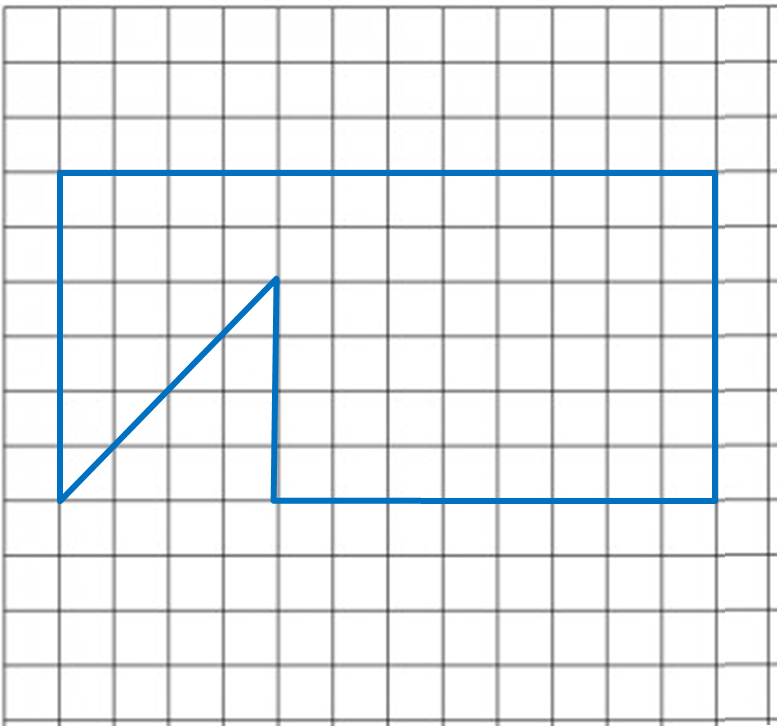
Diagram 2.1 Diagram 2.2
Diagram 2.2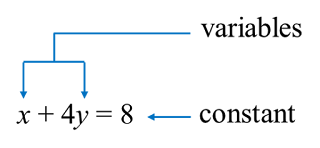
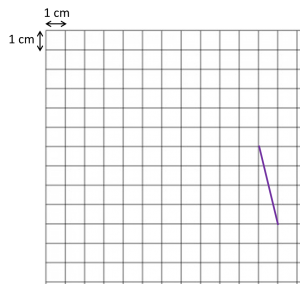
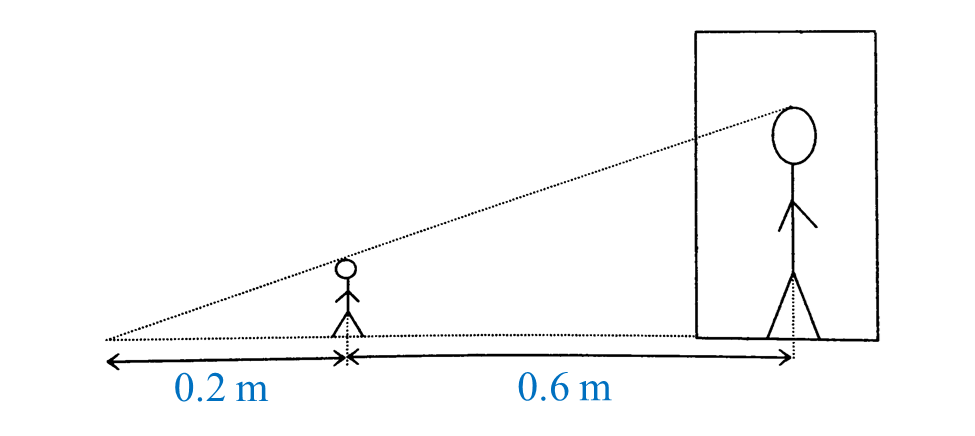 What is the height, in cm, of the puppet used by Tok Dalang?
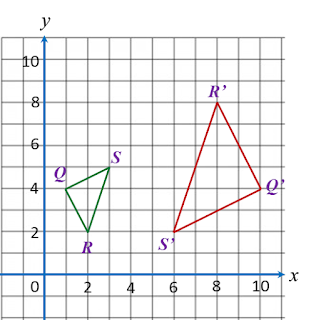
What is the height, in cm, of the puppet used by Tok Dalang?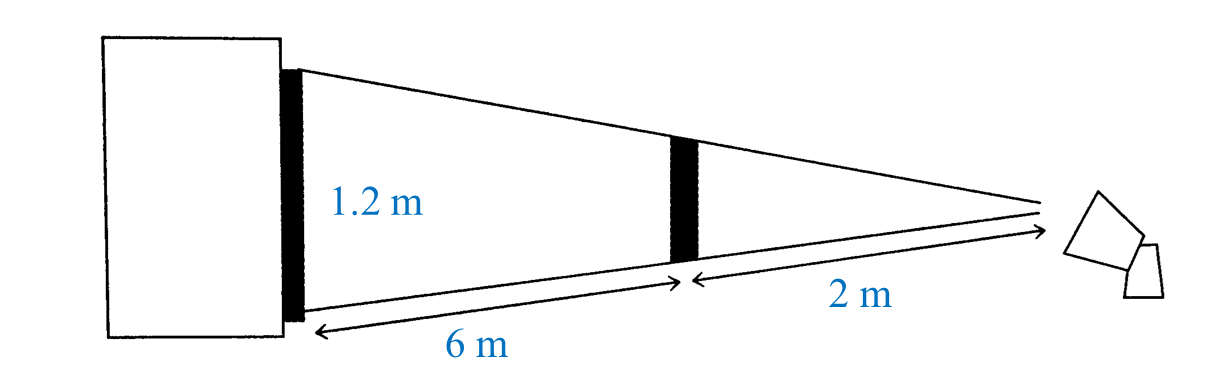 (a) State the scale factor of the enlargement.
(a) State the scale factor of the enlargement.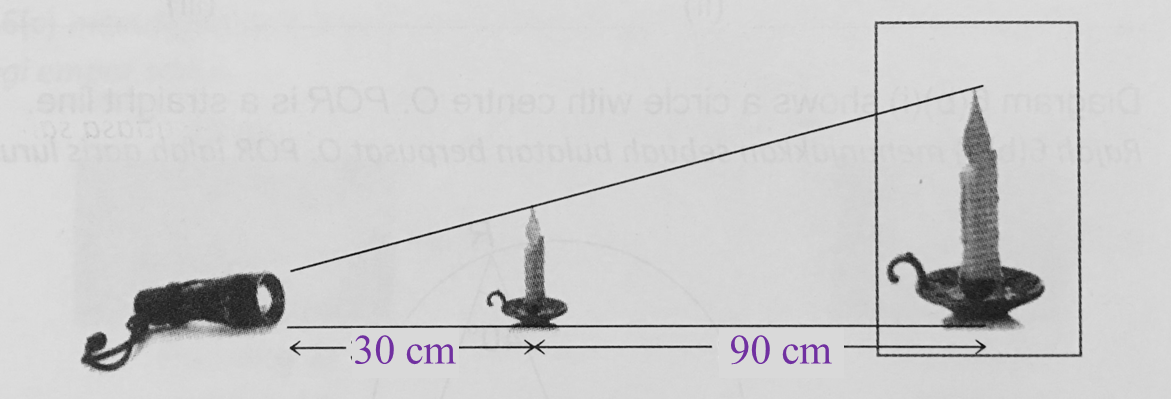







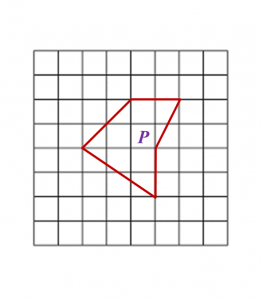




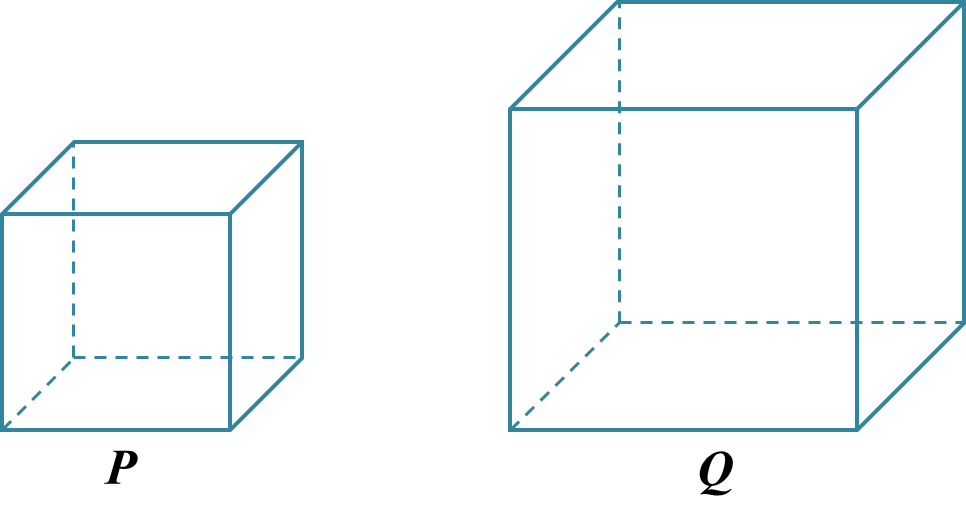 Find the difference in volume between cube P and cube Q.
Find the difference in volume between cube P and cube Q.


