Home › SPM Add Maths › Coordinate Geometry › 6.2 Division of a Line Segment

6.2 Division of a Line Segment

Posted on by

6.2 Division of a Line Segment

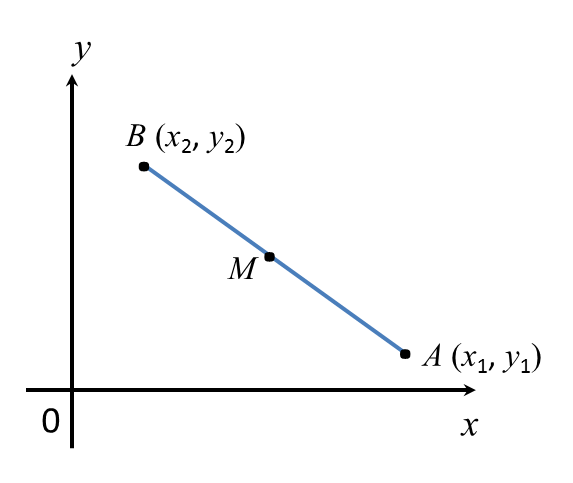
(A) Midpoints of a Line Segment


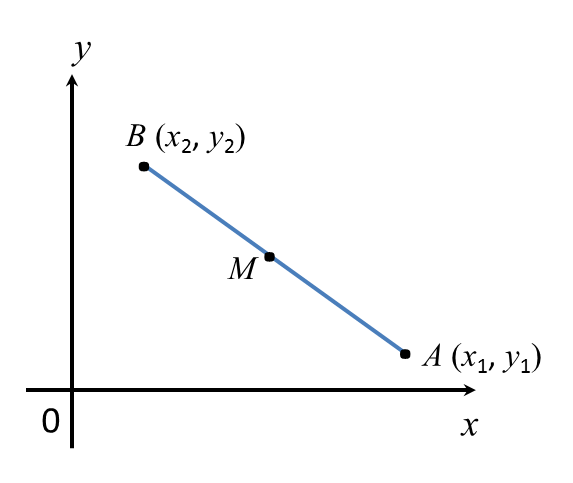
Formula for the midpoint, M of A (xl, y1) and B (x2, y2) is




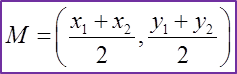
Example 1:
Given B (m – 4, 3) is the midpoint of the straight line joining A(–1, n) and C (5, 8). Find the values of m and n.

Solution:

B  is the midpoint of  A C ( m − 4 ,   3 ) = ( − 1 + 5 2 ,   n + 8 2 ) ( m − 4 ,   3 ) = ( 2 ,   n + 8 2 ) m − 4 = 2  and n + 8 2 = 3 m = 6 and    n + 8 = 6    n = − 2


(B) Point that Internally Divides a Line Segment in the Ratio m : n



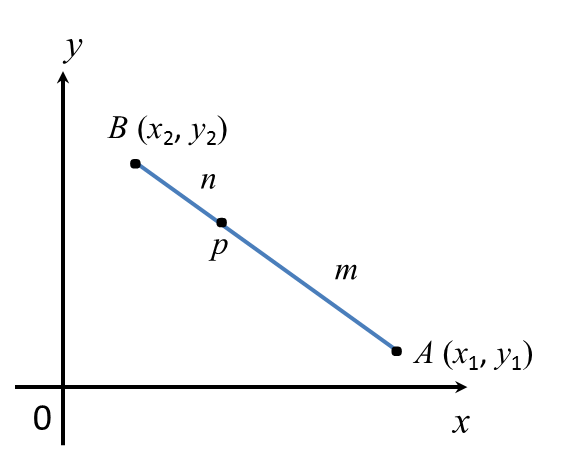
Formula for the point P that lies on AB such that AP : PB = m : n is




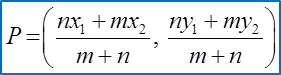
Example 2:
The coordinate of R(2, –1) divide internally the line of AB with the ratio 3 : 2. If coordinate of A is (–1, 2), find the coordinate of B.

Solution:


Let point  B = ( p ,   q ) ( 2 ( − 1 ) + 3 p 3 + 2 ,   2 ( 2 ) + 3 q 3 + 2 ) = ( 2 , − 1 ) ( − 2 + 3 p 5 ,   4 + 3 q 5 ) = ( 2 , − 1 ) Equating the  x -coordinates, − 2 + 3 p 5 = 2 − 2 + 3 p = 10 3 p = 12 p = 4 Equating the  y -coordinates, 4 + 3 q 5 = − 1 4 + 3 q = − 5 3 q = − 9 q = − 3 ∴  The coordinates of point  B = ( 4 , − 3 ) .