Long Questions (Question 1)

Posted on April 21, 2020 by user

Question 1:

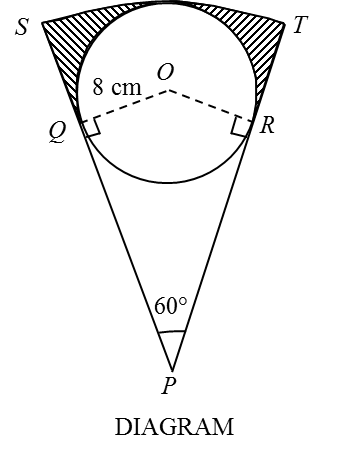
Diagram shows a circle, centre O and radius 8 cm inscribed in a sector SPT of a circle at centre P. The straight lines, SP and TP, are tangents to the circle at point Q and point R, respectively.

[Use p= 3.142]

Calculate

(a) the length, in cm, of the arc ST,

(b) the area, in cm², of the shaded region.

Solution:
(a)

\begin{array}{l} For triangle O P Q \\ \sin 30^{\circ} = \frac{8}{O P} \\ O P = \frac{8}{\sin 30^{\circ}} = 16 cm \\ Radius of sector S P T = 16 + 8 = 24 cm \\ ∠ S P T = 60 \times \frac{3.142}{180} = 1.047 radian \\ Length of arc S T = 24 \times 1.047 = 25.14 cm \end{array}

(b)

\begin{array}{l} For triangle O P Q : \\ \tan 30^{\circ} = \frac{8}{Q P} \\ P Q = \frac{8}{\tan 30^{\circ}} = 13.86 cm \\ ∠ Q O R = 2 (60^{\circ}) = 120^{\circ} \\ Reflex angle ∠ Q O R = 360^{\circ} - 120^{\circ} = 240^{\circ} \\ 240^{\circ} = \frac{3.142}{180^{\circ}} \times 240^{\circ} = 4.189 radian \\ Area of shaded region \\ = (\begin{array}{l} Area of \\ sector S P T \end{array}) - (\begin{array}{l} Area of major \\ sector O Q R \end{array}) - (\begin{array}{l} Area of triangle \\ O P Q and O P R \end{array}) \\ = \frac{1}{2} {(24)}^{2} (1.047) - \frac{1}{2} {(8)}^{2} (4.189) - 2 (\frac{1}{2} \times 8 \times 13.86) \\ = 301.54 - 134.05 - 110.88 \\ = 56.61 {cm}^{2} \end{array}