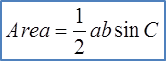Example:
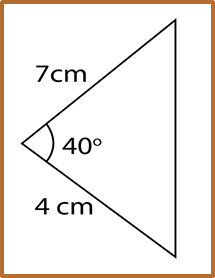
Calculate the area of the triangle above.
Solution:
Area=12absinCArea=12(7)(4)sin40oArea=9 cm2
Calculate the area of the triangle above.
Solution:
Area=12absinCArea=12(7)(4)sin40oArea=9 cm2
Example:
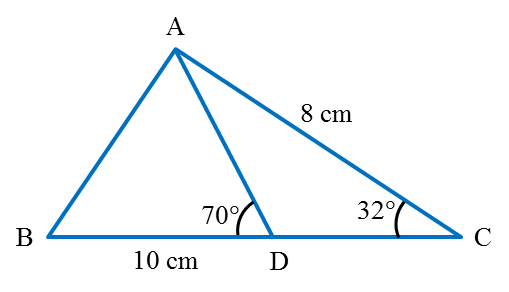
Diagram above shows a triangle ABC, where AC = 8 cm and ∠C = 32o. Point D lies on straight line BC where BD = 10 cm and ∠ADB = 70o . Calculate
(a) the length, in cm, of CD,
(b) the area, in cm2 of ∆ ADC,
(c) the area, in cm2 of ∆ ABC,
(d) the length, in cm, of AB.
Solution:
(a)
∠ADC+70o=180o∠ADC=110o∠CAD=180o−110o−32o∠CAD=38oUsing Sine Rule,8sin110o=CDsin38oCDsin110o=8sin38oCD(0.940)=8(0.616)CD=5.243
(b)
Area of △ADC=12(8)(5.243)sin32o=20.972(0.530)=11.12 cm2
(c)
Area of △ABC=12(8)(10+5.243)sin32o=60.972(0.530)=32.315 cm2
(d)
Use Cosine Rule for △ABC,AB2=15.2432+82−2(15.243)(8)cos32oAB2=232.35+64−206.83AB2=89.52AB=9.462 cm

Diagram above shows a triangle ABC, where AC = 8 cm and ∠C = 32o. Point D lies on straight line BC where BD = 10 cm and ∠ADB = 70o . Calculate
(a) the length, in cm, of CD,
(b) the area, in cm2 of ∆ ADC,
(c) the area, in cm2 of ∆ ABC,
(d) the length, in cm, of AB.
Solution:
(a)
∠ADC+70o=180o∠ADC=110o∠CAD=180o−110o−32o∠CAD=38oUsing Sine Rule,8sin110o=CDsin38oCDsin110o=8sin38oCD(0.940)=8(0.616)CD=5.243
(b)
Area of △ADC=12(8)(5.243)sin32o=20.972(0.530)=11.12 cm2
(c)
Area of △ABC=12(8)(10+5.243)sin32o=60.972(0.530)=32.315 cm2
(d)
Use Cosine Rule for △ABC,AB2=15.2432+82−2(15.243)(8)cos32oAB2=232.35+64−206.83AB2=89.52AB=9.462 cm