5.3.4 Sketching Graphs of Trigonometric Functions (Part 3)
Example 2:
(a) Sketch the graph y = –½ cos x for 0 ≤ x ≤ 2π.
(b) Hence, using the same axes, sketch a suitable graph to find the number of solutions to the equation
π2x+cosx=0
for 0 ≤ x ≤ 2π.
State the number of solutions.
Solution:
(a)
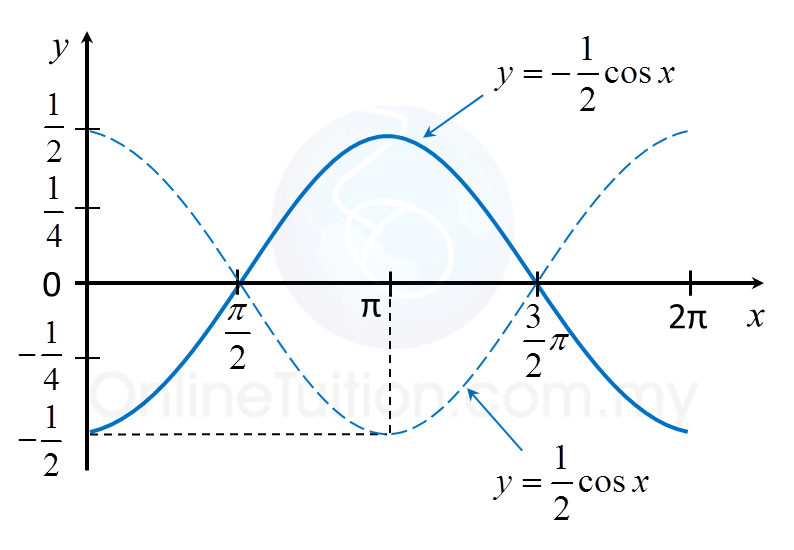

(b)
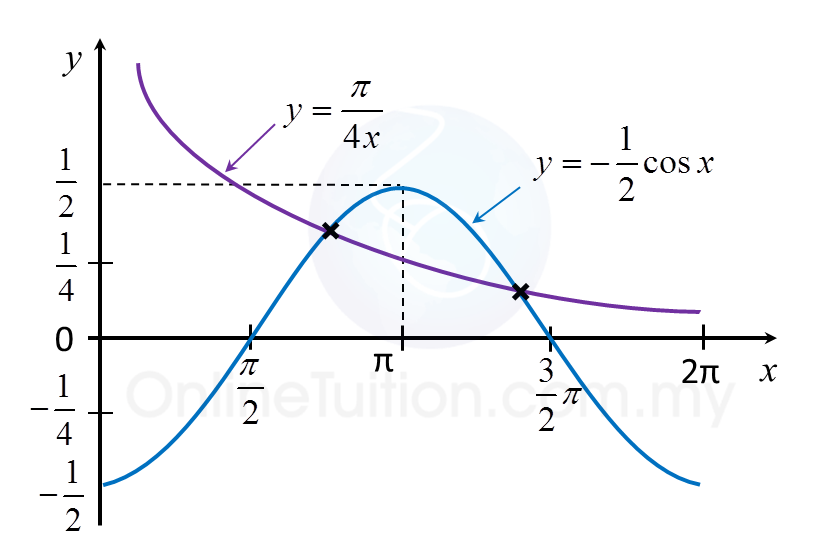

π2x+cosx=0π2x=−cosxπ4x=−12cosx←Multiply both sides by12y=π4x←y=−12cosx
The suitable graph to draw is y=π4x.
x |
π2
|
π |
2π |
y=π4x
|
½ |
¼ |
⅛ |
From the graphs, there are two points of intersection for 0 ≤ x ≤ 2π.
Number of solutions = 2.