Question 5:
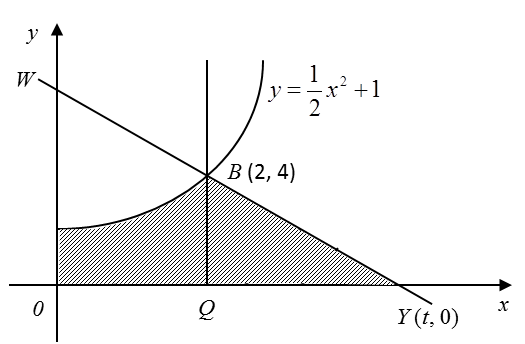
In Diagram below, the straight line WY is normal to the curve y=12x2+1 at B (2, 4). The straight line BQ is parallel to the y–axis.
Find
(a) the value of t,
(b) the area of the shaded region,
(c) the volume generated, in terms of π, when the region bounded by the curve, the y–axis
and the straight line y = 4 is revolved through 360° about the y-axis.
Solution:
(a)
y=12x2+1Gradient of tangent, dydx=2(12x)=xAt point B, dydx=2Gradient of normal, m2=−124−02−t=−128=−2+tt=10
(b)
Area of the shaded region=Area under the curve + Area of triangle BQY=∫20(12x2+1) dx+12(10−2)(4)=[x36+x]20+16=[86+2]−0+16=1913 unit2
(c)
At y−axis, x=0, y=12(0)+1=1y=12x2+1, x2=2y−2Volume generated = π∫x2dy=π∫41(2y−2) dy=π[y2−2y]41=π[(16−8)−(1−2)]=9π unit3
In Diagram below, the straight line WY is normal to the curve y=12x2+1 at B (2, 4). The straight line BQ is parallel to the y–axis.
Find
(a) the value of t,
(b) the area of the shaded region,
(c) the volume generated, in terms of π, when the region bounded by the curve, the y–axis
and the straight line y = 4 is revolved through 360° about the y-axis.
(a)
y=12x2+1Gradient of tangent, dydx=2(12x)=xAt point B, dydx=2Gradient of normal, m2=−124−02−t=−128=−2+tt=10
(b)
Area of the shaded region=Area under the curve + Area of triangle BQY=∫20(12x2+1) dx+12(10−2)(4)=[x36+x]20+16=[86+2]−0+16=1913 unit2
(c)
At y−axis, x=0, y=12(0)+1=1y=12x2+1, x2=2y−2Volume generated = π∫x2dy=π∫41(2y−2) dy=π[y2−2y]41=π[(16−8)−(1−2)]=9π unit3