(Long Questions) – Question 1

Posted on April 22, 2020 by user

Question 1:

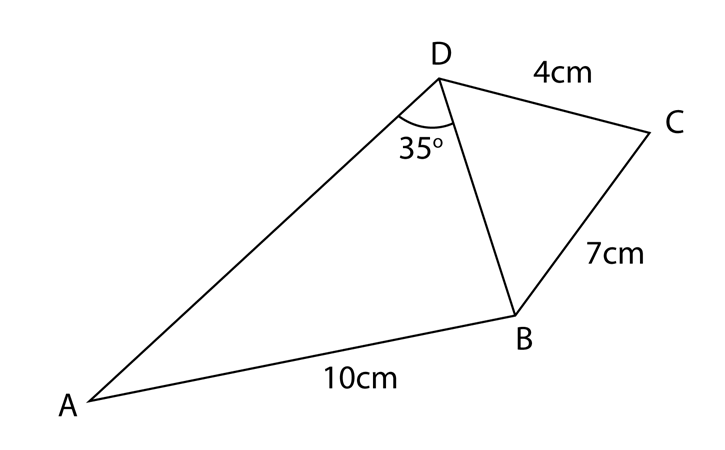
The diagram shows a quadrilateral ABCD. The area of triangle BCD is 12 cm² and ∠BCD is acute. Calculate

(a) ∠BCD,

(b) the length, in cm, of BD,

(c) ∠ABD,

(d) the area, in cm², quadrilateral ABCD.

Solution:

(a) Given area of triangle BCD = 12 cm²

½ (BC)(CD) sin C = 12

½ (7) (4) sin C = 12

14 sin C = 12

sin C = 12/14 = 0.8571

C = 59^o

∠BCD = 59^o

(b)
Using cosine rule,

BD² = BC² + CD² – 2 (7)(4) cos 59^o

BD² = 7²+ 4² – 2 (7)(4) cos 59^o

BD² = 65 – 28.84

BD² = 36.16

BD = 36.16
BD = 6.013 cm

(c)
Using sine rule,

\begin{array}{l} \frac{A B}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \frac{10}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \sin A = \frac{6.013 \times \sin 35^{\circ}}{10} \\ \sin A = 0.3449 \\ A = {20.18}^{\circ} \\ ∠ A B D = 180^{\circ} - 35^{\circ} - {20.18}^{\circ} \\ ∠ A B D = {124.82}^{\circ} \end{array}

(d)
Area of quadrilateral ABCD

= Area of triangle ABD + Area of triangle BCD

= ½ (AB)(BD) sin B + 12 cm

= ½ (10) (6.013) sin 124.82 + 12

= 24.68 + 12

= 36.68 cm²