Question 2:
It is given that BG= 40cm, GA = 33 cm, AH = 30 cm, GAH = 85o and JBK= 45o.
Solution:
(a)(i)
(b)
(c)
In the diagram below, ABC is a triangle. AGJB, AHC and BKC are straight lines. The straight line JK is perpendicular to BC.
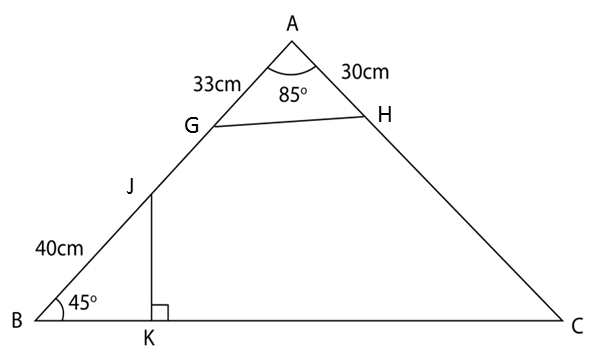

It is given that BG= 40cm, GA = 33 cm, AH = 30 cm, GAH = 85o and JBK= 45o.
(a) Calculate the length, in cm of
i. GH
ii. HC
(b) The area of triangle GAH is twice the area of triangle JBK. Calculate the length, in cm,
of BK.
(c) Sketch triangle which has a different shape from triangle ABC such that, A’B’ = AB,
A’C’ = AC and ∠A’B’C’ = ∠ABC.
(a)(i)
Using cosine rule,
GH2 = AG2 + AH2 – 2 (AG)(AH) ∠GAH
GH2 = 332+ 302 – 2 (33)(30) cos 85o
GH2 = 1089 + 900 – 172.57
GH2 = 1816.43
GH = 42.62 cm
(a)(ii)
∠ACD=180∘−45∘−85∘=50∘Using sine rule,ACsin45∘=73sin50∘AC=73×sin45∘sin50∘AC=67.38 cm∴
(b)
(c)
