(Long Questions) – Question 3

Posted on April 22, 2020 by user

Question 3:

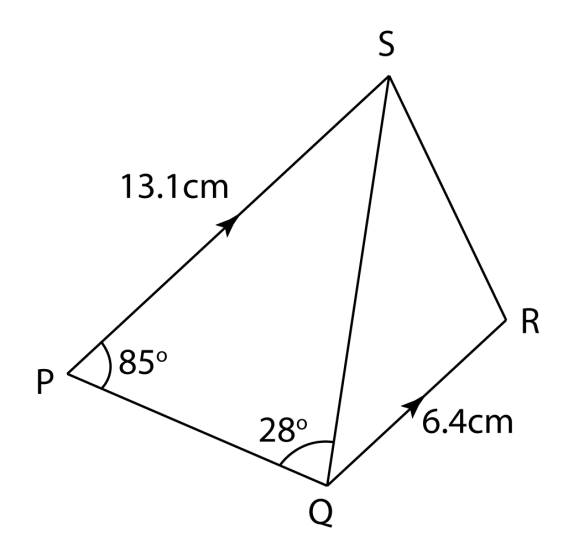
The diagram shows a trapezium PQRS. PS is parallel to QR and QRS is obtuse. Find

(a) the length, in cm, of QS,

(b) the length, in cm, of RS,

(c) ∠QRS,

(d) the area, in cm², of triangle QRS.

Solution:
(a)

$\begin{array}{l} \frac{Q S}{\sin P} = \frac{P S}{\sin Q} \\ \frac{Q S}{\sin 85^{\circ}} = \frac{13.1}{\sin 28^{\circ}} \\ Q S = \frac{13.1 \times \sin 85^{\circ}}{\sin 28^{\circ}} \\ Q S = 27.8 cm \end{array}$

(b)
∠RQS = 180^o – 85^o – 28^o

∠RQS = 67^o

Using cosine rule,

RS² = QR² + QS² – 2 (QR)(QS) ∠RQS

RS² = 6.4² + 27.8² – 2 (6.4)(27.8) cos 67^o

RS² = 813.8 – 139.04

RS² = 674.76

RS = 25.98 cm

(c)

$\begin{array}{l} Using cosine rule, \\ Q S^{2} = Q R^{2} + R S^{2} - 2 (Q R) (R S) \cos ∠ Q R S \\ {27.8}^{2} = {6.4}^{2} + {25.98}^{2} - 2 (6.4) (25.98) \cos ∠ Q R S \\ 772.84 = 715.92 - 332.54 \cos ∠ Q R S \\ \cos ∠ Q R S = \frac{715.92 - 772.84}{332.54} \\ \cos ∠ Q R S = - 0.1712 \\ ∠ Q R S = {99.86}^{\circ} \end{array}$

(d)
Area of triangle QRS

= ½ (QR)(RS) sin R

= ½ (6.4) (25.98) sin 99.86^o

= 81.91 cm²