Question 4:
Diagram below shows a quadrilateral PQRS.
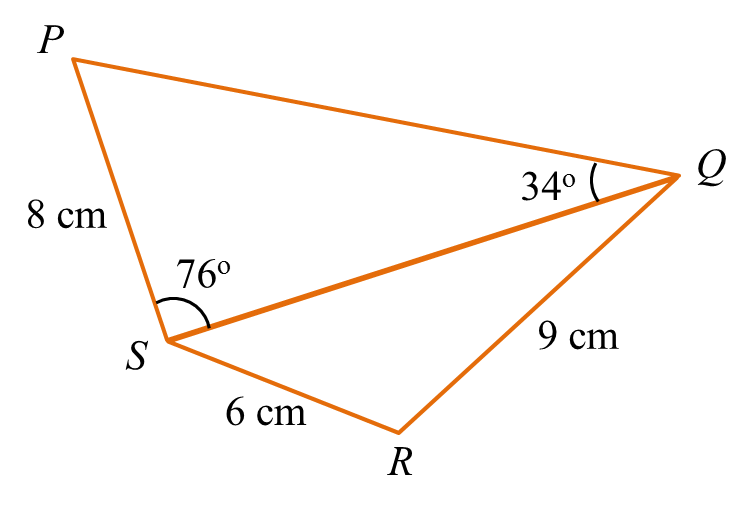
(a) Find
(i) the length, in cm, of QS.
(ii) ∠QRS.
(iii) the area, in cm2, of the quadrilateral PQRS.
(b)(i) Sketch a triangle S’Q’R’ which has a different shape from triangle SQR such that S’R’ = SR, S’Q’ = SQ and ∠S’Q’R’ = ∠SQR.
(ii) Hence, state ∠S’R’Q’.
Solution:
(a)(i)
∠P=180−76−34=70QSsin70=8sin34QS=8×sin70sin34 =13.44 cm
(a)(ii)
13.442=62+92−2(6)(9)cos∠QRS108cos∠QRS=62+92−13.442cos∠QRS=62+92−13.442108 ∠QRS=cos−1(−0.5892) =126o6'
(a)(iii)
Area of PQRS=Area of PQS+Area of QRS=(12×8×13.44×sin76)+(12×6×9×sin126o6')=52.16+21.82=73.98 cm2
(b)(i)
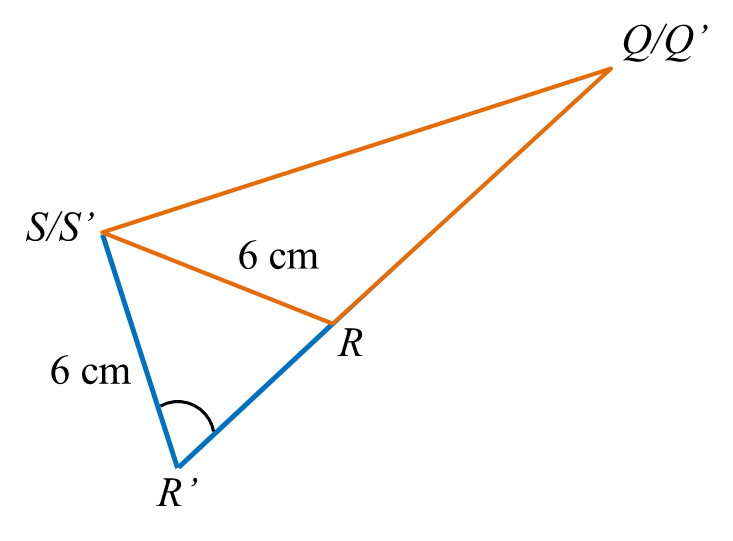
(b)(ii)
∠S'R'Q'=∠S'RR' =180−126o6' =53o54'
Diagram below shows a quadrilateral PQRS.

(a) Find
(i) the length, in cm, of QS.
(ii) ∠QRS.
(iii) the area, in cm2, of the quadrilateral PQRS.
(b)(i) Sketch a triangle S’Q’R’ which has a different shape from triangle SQR such that S’R’ = SR, S’Q’ = SQ and ∠S’Q’R’ = ∠SQR.
(ii) Hence, state ∠S’R’Q’.
Solution:
(a)(i)
∠P=180−76−34=70QSsin70=8sin34QS=8×sin70sin34 =13.44 cm
(a)(ii)
13.442=62+92−2(6)(9)cos∠QRS108cos∠QRS=62+92−13.442cos∠QRS=62+92−13.442108 ∠QRS=cos−1(−0.5892) =126o6'
(a)(iii)
Area of PQRS=Area of PQS+Area of QRS=(12×8×13.44×sin76)+(12×6×9×sin126o6')=52.16+21.82=73.98 cm2
(b)(i)

(b)(ii)
∠S'R'Q'=∠S'RR' =180−126o6' =53o54'