(Long Questions) – Question 5

Posted on April 22, 2020 by user

Question 5:

The diagram below shows a triangle ABC.

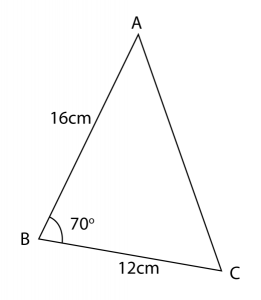
(a) Calculate the length, in cm, of AC.

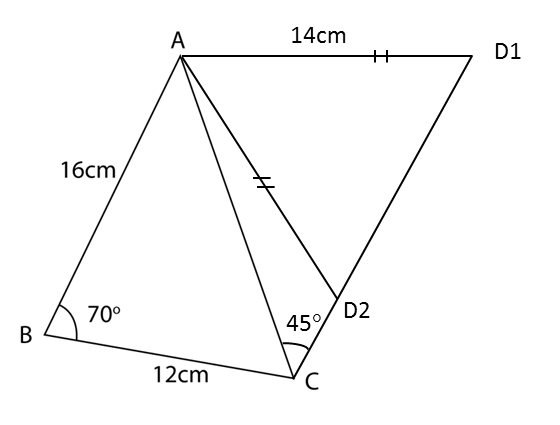
(b) A quadrilateral ABCD is now formed so that AC is a diagonal, ∠ACD = 45° and AD = 14 cm. Calculate the two possible values of ∠ADC.

(c) By using the acute ∠ADC from (b), calculate

(i) the length, in cm, of CD,

(ii) the area, in cm², of the quadrilateral ABCD

Solution:
(a)

Using cosine rule,

AC² = AB² + BC² – 2 (AB)(BC) ∠ABC

AC² = 16² + 12² – 2 (16)(12) cos 70^o

AC² = 400 – 131.33

AC² = 268.67

AC = 16.39 cm

(b)

$\begin{array}{l} Using sine rule, \\ \frac{\sin ∠ A D C}{16.39} = \frac{\sin 45^{\circ}}{14} \\ \sin ∠ A D C = \frac{16.39 \times \sin 45^{\circ}}{14} \\ \sin ∠ A D C = 0.8278 \\ ∠ A D C = {55.87}^{\circ} or (180^{\circ} - {55.87}^{\circ}) \\ ∠ A D C = {55.87}^{\circ} or 124 {.13}^{\circ} \end{array}$

(c)(i)

$\begin{array}{l} Acute angle of ∠ A D C = {55.87}^{\circ} \\ ∠ C A D = 180^{\circ} - 45^{\circ} - {55.87}^{\circ} = {79.13}^{\circ} \\ \frac{C D}{\sin {79.13}^{\circ}} = \frac{14}{\sin 45^{\circ}} \\ C D = \frac{14 \times \sin {79.13}^{\circ}}{\sin 45^{\circ}} = 19.44 cm \end{array}$

(c)(ii)

$\begin{array}{l} Area of quadrilateral A B C D \\ = Area of Δ A B C + Area of Δ A C D \\ = \frac{1}{2} (16) (12) \sin 70^{\circ} + \frac{1}{2} (16.39) (14) \sin {79.13}^{\circ} \\ = 90.21 + 112.67 \\ = 202.88 {cm}^{2} \end{array}$