Question 6:
Diagram below shows trapezium ABCD.
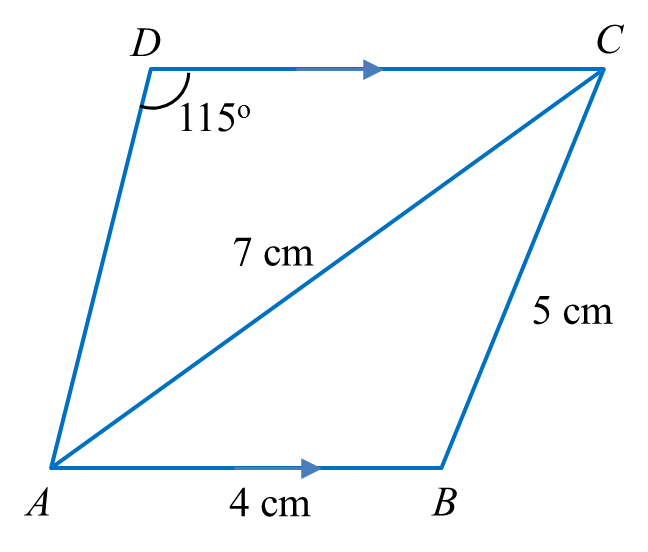 (a) Calculate
(a) Calculate
(i) ∠BAC.
(ii) the length, in cm, of AD.
(b) The straight line AB is extended to B’ such that BC = B’C.
(i) Sketch the trapezium AB’CD.
(ii) Calculate the area, in cm2, of ∆BB’C.
Solution:
(a)(i)
52=42+72−2(4)(7)cos∠BAC25=16+49−56cos∠BAC56cos∠BAC=40cos∠BAC=4056 ∠BAC=cos−14056 =44o25'
(a)(ii)
ADsin∠DCA=7sin115oADsin44o25'=7sin115o←(∠DCA=∠BAC) AD=7sin115o×sin44o25' AD=5.406 cm
(b)(i)
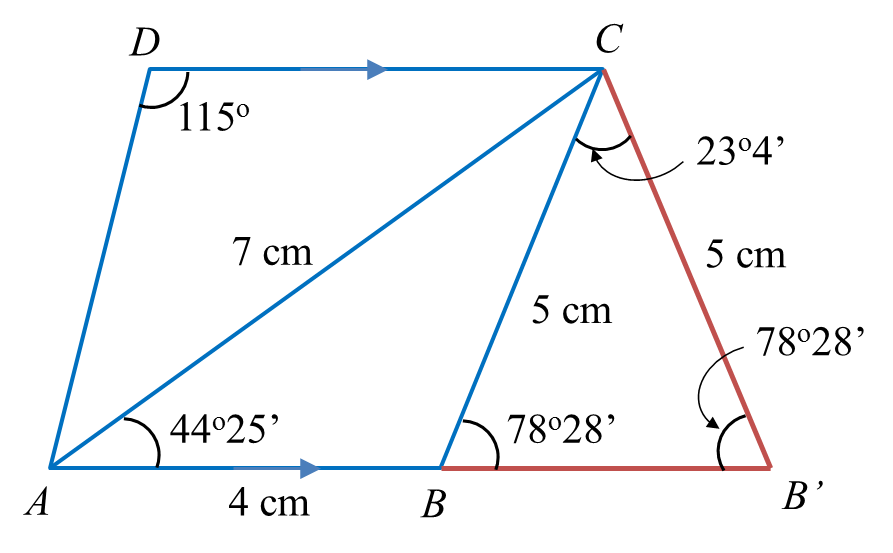
(b)(ii)
sin∠ABC7=sin44o25'5sin∠ABC=sin44o25'5×7 =78o28'∠ABC=180o−78o28'∠ABC=101o32'(obtuse angle)∠CBB'=180o−101o32'=78o28'∠BCB'=180o−78o28'−78o28'=23o4'Area of △BB'C=12×5×5×23o4' =4.898 cm2
Diagram below shows trapezium ABCD.
 (a) Calculate
(a) Calculate(i) ∠BAC.
(ii) the length, in cm, of AD.
(b) The straight line AB is extended to B’ such that BC = B’C.
(i) Sketch the trapezium AB’CD.
(ii) Calculate the area, in cm2, of ∆BB’C.
Solution:
(a)(i)
52=42+72−2(4)(7)cos∠BAC25=16+49−56cos∠BAC56cos∠BAC=40cos∠BAC=4056 ∠BAC=cos−14056 =44o25'
(a)(ii)
ADsin∠DCA=7sin115oADsin44o25'=7sin115o←(∠DCA=∠BAC) AD=7sin115o×sin44o25' AD=5.406 cm
(b)(i)

(b)(ii)
sin∠ABC7=sin44o25'5sin∠ABC=sin44o25'5×7 =78o28'∠ABC=180o−78o28'∠ABC=101o32'(obtuse angle)∠CBB'=180o−101o32'=78o28'∠BCB'=180o−78o28'−78o28'=23o4'Area of △BB'C=12×5×5×23o4' =4.898 cm2