Question 1:
List all the subsets of set P = {r, s}.
Solution:
There are 2 elements, so the number of subsets of set P is 2n = 22 = 4.
Set P = {r, s}
Therefore subsets of set P = {r}, {s}, {r, s}, {}
Question 2:
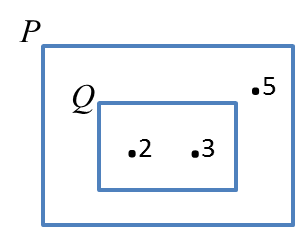
Diagram above shows a Venn diagram with the universal set, ξ = Q ∪ P. List all the subset of set P.
Solution:
Set P has 3 elements, so the number of subsets of set P is 2n = 23 = 8.
Set P = {2, 3, 5}
Therefore subsets of set P = {}, {2}, {3}, {5}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}.
Question 3:
It is given that the universal set, ξ = {x : 30 ≤ x < 42, x is an integer} and set P = {x : x is a number such that the sum of it its two digits is an even number}.
Find set P’.
Solution:
ξ = {30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41}
P = {31, 33, 35, 37, 39, 40}
Therefore P’ = {30, 32, 34, 36, 38, 41}
Question 4:
Given that universal set ξ = {x : 3 < x ≤ 16, x is an integer},
Set A = {4, 11, 13, 16},
Set B = {x : x is an odd number} and
Set C = {x : x is a multiple of 3}.
The elements of the set (A ∪ C)’ ∩ B are
Solution:
ξ = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
A = {4, 11, 13, 16}
B = {5, 7, 9, 11, 13, 15}
C = {6, 9, 12, 15}
(A∪C)' = {5, 6, 7, 8, 10, 14}
Therefore (A∪C)’ ∩ B = {5, 7}