9.3 SPM Practice (Short Questions)

Question 1:

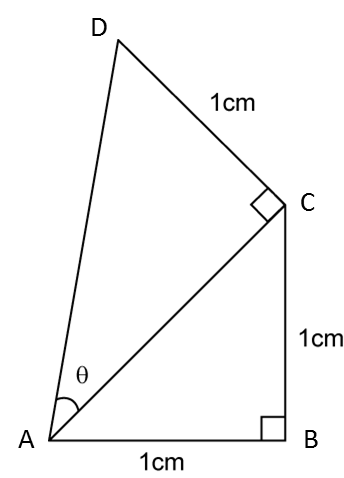
In the diagram above, find the value of tan θ.

Solution:

\begin{array}{l} In △ A B C, using Pythagoras' Theorem, \\ A C = \sqrt{1^{2} + 1^{2}} = \sqrt{2} c m \\ \tan θ = \frac{C D}{A C} \\ \tan θ = \frac{1}{\sqrt{2}} \end{array}

Question 2:

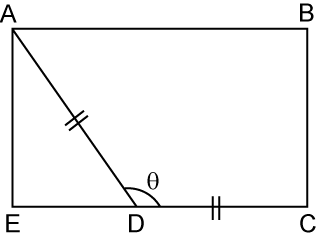
In the diagram above, ABCE is a rectangle and point D lies on the straight line EC. Given that DC = 5 cm and AE = 4cm, find the value of cosθ.

Solution:

\begin{array}{l} A D = D C = 5 c m \\ In △ A E D, using Pythagoras' Theorem, \\ E D = \sqrt{5^{2} - 4^{2}} = 3 c m \\ \cos θ = - \cos ∠ A D E \leftarrow \begin{array}{l} Since 90^{\circ} < θ < 180^{\circ} \\ (in quadrant II), \cos θ is negative \end{array} \\ \cos θ = - \frac{E D}{A D} \\ \cos θ = - \frac{3}{5} \end{array}

Question 3:

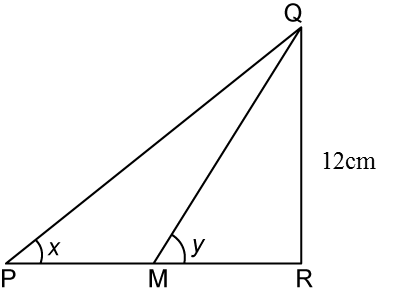
In the diagram above, PMR is a straight line, M is the midpoint of line PR. Given that QR = 12cm and sin y°= 0.6, find the value of tan x°.

Solution:

\begin{array}{l} In triangle Q M R, \\ \sin y^{\circ} = 0.6 \\ \sin y^{\circ} = \frac{Q R}{Q M} = \frac{6}{10} \\ Given Q R = 12 c m, ∴ Q M = 10 \times 2 = 20 c m \\ In △ Q M R, using Pythagoras' Theorem, \\ M R = \sqrt{20^{2} - 12^{2}} = 16 c m \\ P R = 16 \times 2 = 32 c m \\ Hence \tan x^{\circ} = \frac{Q R}{P R} = \frac{12}{32} = \frac{3}{8} \end{array}