Long Questions (Question 1)

Posted on April 23, 2020 by user

Question 1:

Peter, William and Roger compete with each other in shooting a target. The probabilities that they strike the target are

\frac{2}{5}, \frac{3}{4} and \frac{2}{3}

respectively. Calculate the probability that

(a) all the three of them strike the target,

(b) only one of them strikes the target,

Solution:

Let S = Strike and M = Missed

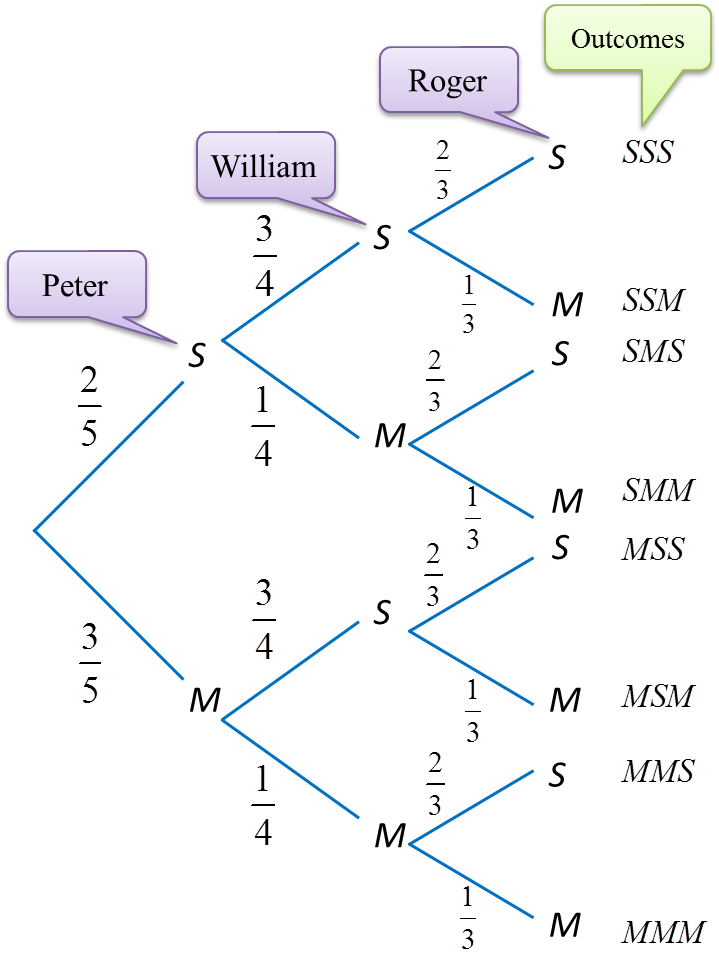
\begin{array}{l} Probability of Peter missed the target = \frac{3}{5} \\ Probability of William missed the target = \frac{1}{4} \\ Probability of Roger missed the target = \frac{1}{3} \end{array}

(a)

\begin{array}{l} Probability (all three persons strike the target) \\ = \frac{2}{5} \times \frac{3}{4} \times \frac{2}{3} \\ = \frac{1}{5} \end{array}

(b)

\begin{array}{l} Probability (only one of them strikes the target) \\ = P (only Peter struck) + P (only William struck) + P (only Roger struck) \\ = (\frac{2}{5} \times \frac{1}{4} \times \frac{1}{3}) + (\frac{3}{5} \times \frac{3}{4} \times \frac{1}{3}) + (\frac{3}{5} \times \frac{1}{4} \times \frac{2}{3}) \\ = \frac{1}{30} + \frac{3}{20} + \frac{1}{10} \\ = \frac{17}{60} \end{array}

(c)

\begin{array}{l} Probability (at least one of them strikes the target) \\ = 1 - P (all missed the target) \\ = 1 - (\frac{3}{5} \times \frac{1}{4} \times \frac{1}{3}) \\ = 1 - \frac{1}{20} \\ = \frac{19}{20} \end{array}