Question 5:
Solution:
(b)
(c)
(d)
y=24x-------------- (1)2x2+5x=24------ (2)(2)÷x,2x+5=24x-------- (3)(1)−(3),y−(2x+5)=0y=2x+5
The suitable straight line is y = 2x + 5.
(a) The following table shows the corresponding values of x and y for the equation
y=24x
x |
–4 |
–3 |
–2 |
–1 |
1 |
1.5 |
2 |
3 |
4 |
y |
–6 |
k |
–12 |
–24 |
24 |
n |
12 |
8 |
6 |
Calculate the value of k and n.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of
y=24x
for –4 ≤ x ≤ 4.
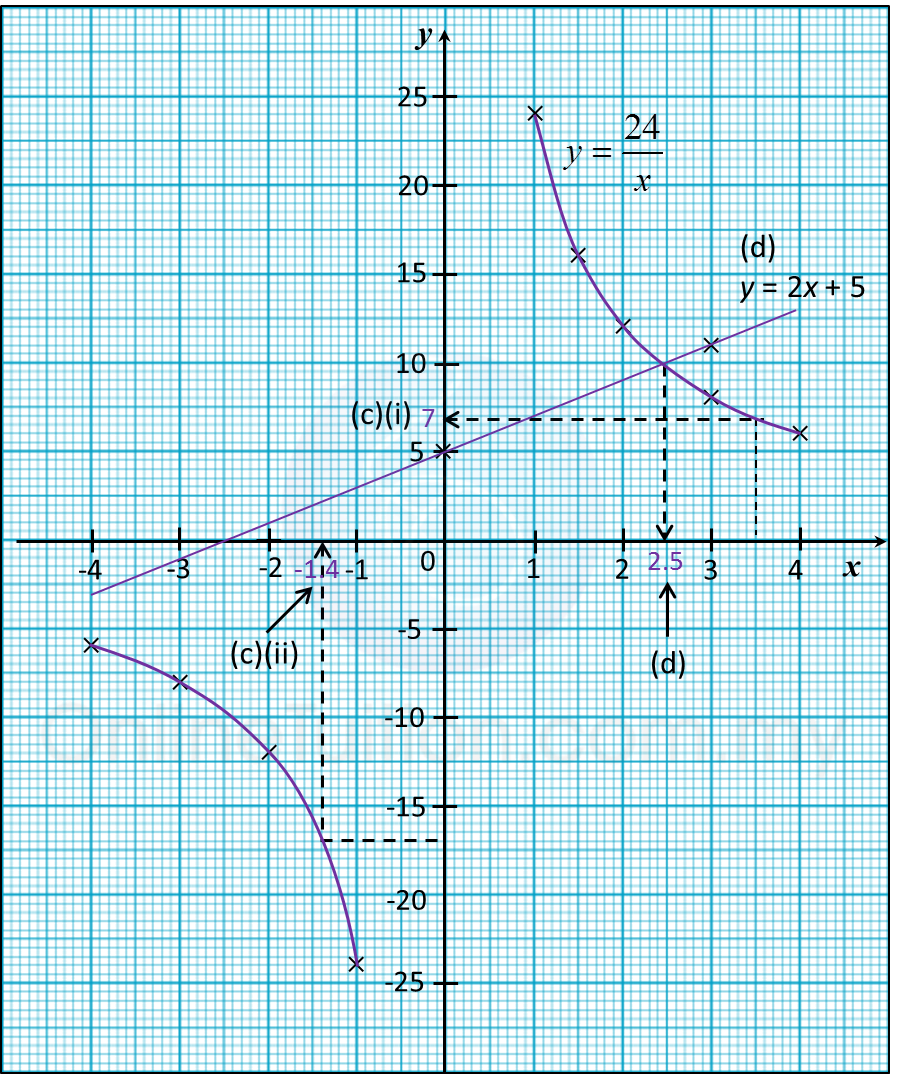
(c) From your graph, find
(i) The value of y when x = 3.5,
(ii) The value of x when y = –17.
(d) Draw a suitable straight line on your graph to find the value of x which satisfy the equation 2x2 + 5x = 24 for –4 ≤ x ≤ 4.
(a)
y=24xwhen x=−3,k=24−3=−8when x=1.5,n=241.5=16
y=24xwhen x=−3,k=24−3=−8when x=1.5,n=241.5=16
(b)

(c)
(i) From the graph, when x = 3.5, y = 7
(ii) From the graph, when y = –17, x = –1.4
(d)
y=24x-------------- (1)2x2+5x=24------ (2)(2)÷x,2x+5=24x-------- (3)(1)−(3),y−(2x+5)=0y=2x+5
The suitable straight line is y = 2x + 5.
Determine the x-coordinate of the point of intersection of the curve and the straight line y = 2x + 5.
x |
0 |
3 |
y = 2x + 5 |
5 |
11 |
From the graph, x = 2.5