2.1 Quadratic Expression (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

Form a quadratic expression by multiplying each of the following.

(a) (6p – 2)(2p – 1)

(b) (m + 5)(4 – 7m)

Solution:

(a) (6p – 2)(2p – 1)

= (6p)(2p) + (6p)(-1) + (-2)(2p) +(-2)(-1)

= 12p² – 6p – 4p + 2

= 12p² – 10p + 2

(b) (m + 5)(4 – 7m)

= (m)(4) + (m)(-7m) + (5)(4) + (5)(-7m)

= 4m – 7m² + 20 – 35m

= – 7m² – 31m+ 20

= (x)(2x) + (x)(-3) + (2)(2x) + (2)(-3)

= 2x²-3x + 4x – 6

= 2x² + x - 6

Quadratic Equations Long Questions (Question 8 – 10)

Posted on April 23, 2020 by user

Question 8:
Solve the following quadratic equation:
4x (x + 4) = 9 + 16x

Solution:

\begin{array}{l} 4 x (x + 4) = 9 + 16 x \\ 4 x^{2} + 16 x = 9 + 16 x \\ 4 x^{2} - 9 = 0 \\ {(2 x)}^{2} - 3^{2} = 0 \\ (2 x + 3) (2 x - 3) = 0 \\ 2 x + 3 = 0 or 2 x - 3 = 0 \\ 2 x = - 3 2 x = 3 \\ x = - \frac{3}{2} x = \frac{3}{2} \end{array}

Question 9:
Solve the following quadratic equation:
(x + 2)² = 2x + 7

Solution:

\begin{array}{l} {(x + 2)}^{2} = 2 x + 7 \\ x^{2} + 4 x + 4 = 2 x + 7 \\ x^{2} - 2 x - 3 = 0 \\ (x + 1) (x - 3) = 0 \\ x + 1 = 0 or x - 3 = 0 \\ x = - 1 x = 3 \end{array}

Question 10:
Solve the following quadratic equation:

- \frac{2}{3 x - 5} = \frac{x}{3 x - 1}

Solution:

\begin{array}{l} - \frac{2}{3 x - 5} = \frac{x}{3 x - 1} \\ - 2 (3 x - 1) = x (3 x - 5) \\ - 6 x + 2 = 3 x^{2} - 5 x \\ 3 x^{2} - 5 x + 6 x - 2 = 0 \\ 3 x^{2} + x - 2 = 0 \\ (3 x - 2) (x + 1) = 0 \\ 3 x - 2 = 0 or x + 1 = 0 \\ 3 x = 2 x = - 1 \\ x = \frac{2}{3} x = - 1 \end{array}

2.3 Quadratic Equations

Posted on April 23, 2020 by user

2.3 Quadratic Equations

1. Quadratic equations are equations which fulfil the following characteristics:

(a) Have an equal ‘=’ sign

(b) Contain only one unknown

(c) Highest power of the unknown is 2.

For example,

2. The general form of a quadratic equation is written as:

(a)
ax² + bx + c = 0,

where a ≠ 0, b ≠ 0 and c ≠ 0,

example: 4x²+ 13x – 12 = 0

(b)
ax² + bx = 0,

where a ≠ 0, b ≠ 0 but c = 0,

example: 7x²+ 9x = 0

where a ≠ 0, c ≠ 0 but b = 0,

example: 9x²– 3 = 0

Example 1:

Write each quadratic equation in the general form.

(a) x² – 5x = 12

(b) -2 + 5x²– 6x = 0

(d) (x – 2)(x + 6) = 0

(e) 3 – 13x = 4 (x² + 2)

(f)

2 - y = \frac{1 - 3 y}{y}

(g)

\frac{p}{4} = \frac{2 p^{2} - 3}{10}

(h)

\frac{y^{2} + 5}{4} = \frac{y - 1}{2}

(i)

\frac{4 p}{7} = p (7 p - 6)

Solution:

A quadratic equation in the general form is written as ax² + bx + c = 0

(a) x² – 5x = 12

x² – 5x -12 = 0

(b) –2 + 5x²– 6x = 0

5x² – 6x –2 = 0

(c) 7p² – 3p = 4p²+ 4p – 3

7p² – 3p – 4p²– 4p + 3 = 0

3p² – 7p + 3 = 0

(d) (x – 2)(x + 6) = 0

x² + 6x – 2x– 12 = 0

x² + 4x – 12 = 0

(e) 3 – 13x = 4 (x² + 2)

3 – 13x = 4x² + 8

–4x²– 8 + 3 – 13x = 0

–4x² – 13x – 5 = 0

4x² + 13x + 5 = 0

(f)

2 - y = \frac{1 - 3 y}{y}

2y – y²= 1 – 3y

2y – y²– 1 + 3y = 0

– y²+ 5y – 1 = 0

y² – 5y + 1 = 0

(g)

\frac{p}{4} = \frac{2 p^{2} - 3}{10}

10p = 8p² – 12

–8p² + 10p +12 = 0

8p² – 10p – 12 = 0

(h)

\frac{y^{2} + 5}{4} = \frac{y - 1}{2}

2y² + 10 = 4y – 4

2y² – 4y + 10 + 4 = 0
2y² – 4y + 14 = 0

(i)

\frac{4 p}{7} = p (7 p - 6)

4p = 7p (7p– 6)

4p = 49p² – 42p

– 49p² + 42p + 4p = 0

49p² – 46p = 0

Quadratic Equations Long Questions (Question 5 – 7)

Posted on April 23, 2020 by user

Question 5:

Solve the equation:

(m + 2)(m – 4) = 7(m – 4).

Solution:

(m + 2)(m – 4) = 7(m – 4)

m²– 4m + 2m – 8 = 7m – 28

m²– 9m + 20 = 0

(m – 5)(m – 4) = 0

m = 5 or m = 4

Question 6:

Solve the equation:

\frac{- 6 y - 2}{y} = \frac{7}{1 - y}

Solution:

\begin{array}{l} \frac{- 6 y - 2}{y} = \frac{7}{1 - y} \\ (- 6 y - 2) (1 - y) = 7 y \\ - 6 y + 6 y^{2} - 2 + 2 y - 7 y = 0 \\ 6 y^{2} - 11 y - 2 = 0 \\ (6 y + 1) (y - 2) = 0 \\ 6 y + 1 = 0 or y = 2 \\ y = - \frac{1}{6} \end{array}

Question 7:

Solve the equation:

\frac{4 m}{7} = m (8 m - 9)

Solution:

\begin{array}{l} \frac{4 m}{7} = m (8 m - 9) \\ 4 m = 7 m (8 m - 9) \\ 4 m = 56 m^{2} - 63 m \\ 56 m^{2} - 63 m - 4 m = 0 \\ 56 m^{2} - 67 m = 0 \\ m (56 m - 67) = 0 \\ m = 0 or 56 m - 67 = 0 \\ m = \frac{67}{56} \end{array}

2.2 Factorisation of Quadratic Expression

Posted on April 23, 2020 by user

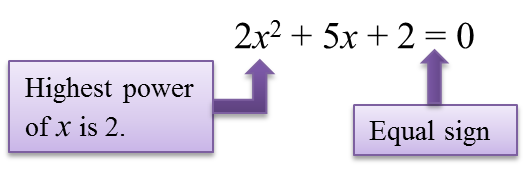
2.2 Factorisation of Quadratic Expression

(A) Factorisation quadratic expressions of the form ax² + bx + c, b = 0 or c = 0

1. Factorisation of quadratic expressions is a process of finding two linear expressions whose product is the same as the quadratic expression.

2. Quadratic expressions ax² + c and ax² + bx that consist of two terms can be factorised by finding the common factors for both terms.

Example 1:

Factorise each of the following:

(a) 2x²+ 6

(b) 7p²– 3p

(c) 6x²– 9x

Solution:

(a) 2x²+ 6 = 2 (x² + 3) ← (2 is common factor)

(b) 7p²– 3p = p (7p – 3) ← (p is common factor)

(c) 6x²– 9x = 3x (2x – 3) ← (3x is common factor)

(B) Factorisation of quadratic expressions in the form ax² – c , where a and c are perfect squares

Example 2:

(a) 9p²– 16

(b) 25x²– 1

(c)

\frac{1}{4} - \frac{1}{25} x^{2}

Solution:

(a) 9p²– 16 = (3p)² – 4²= (3p – 4) (3p + 4)

(b) 25x²– 1 = (5x)² – 1²= (5x – 1) (5x + 1)

(c)

\begin{array}{l} \frac{1}{4} - \frac{1}{25} x^{2} = {(\frac{1}{2})}^{2} - {(\frac{1}{5} x)}^{2} \\ = (\frac{1}{2} - \frac{1}{5} x) (\frac{1}{2} + \frac{1}{5} x) \end{array}

(C) Factorisation quadratic expressions in the form ax² + bx + c, where a ≠ 0, b ≠ 0 and c ≠ 0

Example 3:

Factorise each of the following

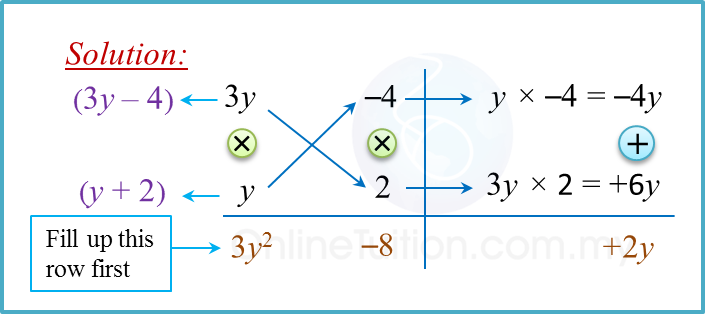
(a) 3y²+ 2y – 8

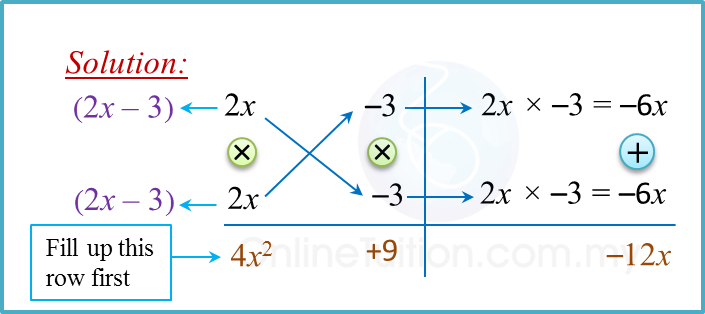
(b) 4x²– 12x + 9

Solution:

(a)

Factorise using the Cross Method

3y²+ 2y – 8 = (3y – 4) (y + 2)

(b)

4x²– 12x + 9 = (2x – 3) (2x – 3)

2.1 Quadratic Expression

Posted on April 23, 2020 by user

(A) Identifying quadratic expression

1. A quadratic expression is an algebraic expression of the form ax² + bx + c, where a, b and c are constants, a ≠ 0 and x is an unknown.

(a) The highest power of x is 2.

(b) For example, 5x²– 6x + 3 is a quadratic expression.

Example 1

State whether each of the following is a quadratic expression in one unknown.

(a) x² – 5x + 3

(b) 8p² + 10

(d) 2x² + 4y + 14

(e)

2 p + \frac{1}{p} + 6

(f) y³ – 3y + 1

Solution:

(a) Yes. A quadratic expression in one unknown.

(b) Yes. A quadratic expression in one unknown.

(c) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

(d) Not a quadratic expression in one unknown. There are 2 unknowns, x and y in the quadratic expression.

(e) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

\frac{1}{p} = p^{- 1}

(f) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

2. A quadratic expression can be formed by multiplying two linear expressions.

(2x + 3)(x - 3) = 2x² – 3x – 9

Example 2

Multiply the following pairs of linear expressions.

(a) (4x + 3)(x – 2)

(b) (y – 6)²

Solution:

(a) (4x + 3)(x – 2)

= (4x)(x) + (4x)(-2) +(3)(x) + (3)(-2)

= 4x² – 8x + 3x – 6

= 4x² – 5x – 6

(b) (y – 6)²

= (y – 6)(y – 6)

= (y)(y) + (y)(-6) + (-6)(y) + (-6)(-6)

= y² -6y – 6y + 36

= y² - 12y + 36

(c) 2x (x – 5)

= 2x(x) + 2x(-5)

= 2x² – 10x

Quadratic Equations Long Questions (Question 1 – 4)

Posted on April 23, 2020 by user

Question 1:

Solve the quadratic equation, (y + 3)(y – 4) = 30

Solution:

(y + 3)(y – 4) = 30

y² – 4y + 3y– 12 = 30

y² – y – 12 – 30 = 0

y² – y – 42 = 0

(y + 6)(y – 7) = 0

y + 6 = 0, y = –6

y – 7 = 0

y = 7

Question 2:

Solve the quadratic equation, 5x² = 3( x – 2) + 8

Solution:

5x² = 3x – 6 + 8

5x² – 3x – 2 = 0

(5x + 2)(x – 1) = 0

5x + 2 = 0, x

- \frac{2}{5}

x – 1 = 0

x = 1

Question 3:

Solve the quadratic equation

\frac{2 p^{2} - 15}{p} = 7

Solution:

\frac{2 p^{2} - 15}{p} = 7

2p² – 15 = 7p

2p² –7p – 15 = 0

(2p + 3)(p – 5) = 0

2p + 3 = 0, p =

- \frac{3}{2}

p – 5 = 0

p = 5

Question 4:

Solve the quadratic equation

y (y - \frac{9}{2}) = \frac{5}{2}

Solution:

\begin{array}{l} y (y - \frac{9}{2}) = \frac{5}{2} \\ y^{2} - \frac{9 y}{2} = \frac{5}{2} \end{array}

( ×2), 2y² – 9y= 5

2y² – 9y – 5 = 0

(2y + 1)(y – 5) = 0

2y + 1 = 0, y = – ½

y – 5 = 0

y = 5

1.1 Significant Figures

Posted on April 23, 2020 by user

1.1.2 Significant Figures (Part 2)

1. Perform combined operations (addition, subtraction, multiplication and division) involving numbers, the final answer is rounded off to specific significant figures.

Example:

Find the value of each of the following and give your answer correct to 3 significant figures.

(a) 261.9 + 75.6 × 0.7

(b) 0.062 × 30.12 + 1.268

(c)

8.608 \div 0.08 - 28.35

(d) 0.846 ÷ 0.4 - 0.153 × 2

Solution:

(a) 261.9 + 75.6 × 0.7

= 261.9 + 52.92

= 314.82
= 315 (3 s. f.)

(b) 0.062 × 30.12 + 1.268

= 1.86744 + 1.268

= 3.13544

= 3.14 (3 s. f.)

(c)

8.608 \div 0.08 - 28.35

= 107.6 – 28.35

= 79.25
= 79.3 (3 s. f.)

(d)

0.846 \div 0.4 - 0.153 \times 2

= 2.115 – 0.306

= 1.809

= 1.81 (3 s. f.)

Example 1:

Calculate the value of 5.33 + 0.33 × 17 and give your answer correct to three significant figures.

Solution:

5.33 + 0.33 × 17

= 5.33 + 5.61

= 10.94

= 10.9 (3 s. f.)

Example 2:

Calculate the value of 49.3567 + 16.73 ÷ 0.5 and give your answer correct to four significant figures.

Solution:

49.3567 + 16.73 ÷ 0.5

= 49.3567 + 33.46

= 82.8167

= 82.82 (4 s. f.)

Example 3:

Calculate the value of 3.42 ÷ 12 × 3.7 and give your answer correct to four significant figures.

Solution:

3.42 ÷ 12 × 3.7

= 1.0545

= 1.055 (4 s. f.)

1.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 1:

Round off each of the following numbers to the number of significant figures indicated in brackets.

(a) 80616 (3 s. f.)

(b) 60932 (3 s. f.)

(c) 0.4783 (2 s. f.)

(d) 3.047 (3 s. f.)

(e) 0.00567 (2 s. f.)

(f) 0.05086 (3 s. f.)

Solution:

(a) 80600

(b) 60900

(c) 0.48

(d) 3.05

(e) 0.0057

(f) 0.0509

Question 2:
Express each of the following as a single numbers.
(a) 8.565 × 10^-5
(b) 1.304 × 10⁵

(c) 6.754 × 10^-6

(d) 1.0352 × 10⁴

Solution:

(a) 0.00008565

(b) 130400

(c) 0.000006754

(d) 10352

Question 3:
Express each of the following in standard form.
(a) 376510
(b) 47865400
(c) 0.000507
(d) 0.00006408

Solution:

(a) 3.7651 × 10⁵

(b) 4.78654 × 10⁷

(c) 5.07 × 10^-4

(d) 6.408 × 10^-5

Question 4:

1.3 × 10¹⁵ + 3.2 × 10¹⁴

Solution:

1.3 × 10¹⁵ + 3.2 × 10¹⁴

= 1.3 × 10¹⁵ + 0.32 × 10¹⁵

= (1.3 +0. 32) × 10¹⁵

= 1.62 × 10¹⁵

Question 5:

0.0000036 – 2.1 × 10^-7

Solution:

0.0000036 – 2.1 × 10^-7

= 3.6 × 10^-6 – 2.1 × 10^-7

= 3.6 × 10^-6 – 0.21 × 10^-6

= (3.6 - 0.21) × 10^-6

= 3.39 × 10^-6

1.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

1.3.2 Standard Form, SPM Practice (Paper 1)

Question 6:

(a) Round off 0.05079 correct to three significant figures.

(b) Find the value of 5 × 10⁷ + 7.2 × 10⁵ and state its answer in standard form.

Solution:

(a) 0.05079 = 0.0508 (correct to three significant figures)

(b) 5 × 10⁷ + 7.2 × 10⁵= 500 × 10⁵ + 7.2 × 10⁵

= (500 + 7.2) × 10⁵

= 507.2 × 10⁵

= 5.072 × 10⁷

Question 7:

(a) Calculate the value of 70.2 – 3.22 × 8.4 and round off its answer correct to three significant figures.

(b) Express

\frac{840}{0.000021}

as a number in standard form.

Solution:

(a) 70.2 – 3.22 × 8.4 = 70.2 – 27.048

= 43.152 = 43.2 (correct to three significant figures)

(b)

\begin{array}{l} \frac{840}{0.000021} = \frac{8.4 \times 10^{2}}{2.1 \times 10^{- 5}} \\ = \frac{8.4}{2.1} \times 10^{2 - (- 5)} \\ = 4 \times 10^{7} \end{array}

Question 8:

Calculate the value of 7 × (2 × 10^-2)³– 4.3 × 10^-5 and state its answer in standard form.

Solution:

7 × (2 × 10^-2)³ – 4.3 × 10^-5= 7 × 2³ × (10^-2)³– 4.3 × 10^-5

= 56 × 10^-6– 4.3 × 10^-5

= 5.6 × 10^-5– 4.3 × 10^-5

= 1.3 × 10^-5