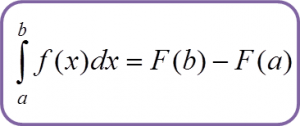Long Question 3

Posted on April 22, 2020 by user

Question 3:

The gradient function of a curve which passes through P(2, –14) is 6x² – 12x.

Find

(a) the equation of the curve,

(b) the coordinates of the turning points of the curve and determine whether each of the turning points is a maximum or a minimum.

Solution:
(a)

$\begin{array}{l} Given gradient function of a curve \frac{d y}{d x} = 6 x^{2} - 12 x \\ The equation of the curve, \\ y = \int (6 x^{2} - 12 x) d x \\ y = \frac{6 x^{3}}{3} - \frac{12 x^{2}}{2} + c \\ y = 2 x^{3} - 6 x^{2} + c \\ - 14 = 2 {(2)}^{3} - 6 {(2)}^{2} + c, at point P (2, - 14) \\ - 14 = - 8 + c \\ c = - 6 \\ y = 2 x^{3} - 6 x^{2} - 6 \end{array}$

(b)

$\begin{array}{l} \frac{d y}{d x} = 6 x^{2} - 12 x \\ At turning points, \frac{d y}{d x} = 0 \\ 6 x^{2} - 12 x = 0 \\ 6 x (x - 2) = 0 \\ x = 0, x = 2 \\ x = 0, y = 2 {(0)}^{3} - 6 {(0)}^{2} - 6 = - 6 \\ x = 2, y = 2 {(2)}^{3} - 6 {(2)}^{2} - 6 = - 14 \\ \frac{d^{2} y}{d x^{2}} = 12 x - 12 \\ When x = 0, \frac{d^{2} y}{d x^{2}} = 12 (0) - 12 = - 12 < 0 \\ (0, - 6) is a maximum point . \\ When x = 2, \frac{d^{2} y}{d x^{2}} = 12 (2) - 12 = 12 > 0 \\ (2, - 14) is a minimum point . \end{array}$

3.5 Integration as the Summation of Areas

Posted on April 22, 2020 by user

3.5 Integration as the Summation of Areas

(A) Area of the region between a Curve and the x-axis.

Area of the shaded region;

$A = \int_{a}^{b} y d x$

(B) Area of the region between a curve and the y-axis.

Area of the shaded region;

$A = \int_{a}^{b} x d y$

(C) Area of the region between a curve and a straight line.

Area of the shaded region;

$A = \int_{a}^{b} f (x) d x - \int_{a}^{b} g (x) d x$

3.2 Integration by Substitution

Posted on April 22, 2020 by user

3.2 Integration by Substitution

It is given that

${\int (a x + b)}^{n} d x, n \neq - 1.$

(A) Using the Substitution method,

$\begin{array}{l} Let u = a x + b \\ Thus, \frac{d u}{d x} = a \\ ∴ d x = \frac{d u}{a} \end{array}$

Example 1:

$\begin{array}{l} {\int (3 x + 5)}^{3} d x . \\ Let u = 3 x + 5 \\ \frac{d u}{d x} = 3 \\ d x = \frac{d u}{3} \\ {\int (3 x + 5)}^{3} d x \\ = \int u^{3} \frac{d u}{3} \leftarrow \begin{array}{l} substitute 3 x + 5 = u \\ and d x = \frac{d u}{3} \end{array} \\ = \frac{1}{3} \int u^{3} d u \\ = \frac{1}{3} (\frac{u^{4}}{4}) + c \\ = \frac{1}{3} (\frac{{(3 x + 5)}^{4}}{4}) + c \leftarrow \begin{array}{l} substitute back \\ u = 3 x + 5 \end{array} \\ = \frac{{(3 x + 5)}^{4}}{12} + c \end{array}$

(B) Using Formula method

$\begin{array}{l} \int {(a x + b)}^{n} = \frac{{(a x + b)}^{n + 1}}{(n + 1) a} + c \\ Hence, \\ \int {(3 x + 5)}^{3} d x = \frac{{(3 x + 5)}^{4}}{4 (3)} + c \\ = \frac{{(3 x + 5)}^{4}}{12} + c \end{array}$

Example 2 (Formula method):

Basic Integration

Posted on April 22, 2020 by user

3.1 Integration as the Inverse of Differentiation, Integration of axⁿ and integration of the Functions of the Sum/Difference of Algebraic Terms

Type 1:

$\begin{array}{l} \int a d x = a x + C \\ Example \\ \int 2 d x = 2 x + C \end{array}$

Type 2:

$\begin{array}{l} \int a x^{n} d x = \frac{a x^{n + 1}}{n + 1} + C \\ E x a m p l e 1 \\ \int 2 x^{3} d x = \frac{2 x^{4}}{4} + C = \frac{x^{4}}{2} + C \\ E x a m p l e 2 \\ \int \frac{2}{3 x^{5}} d x = \int \frac{2}{3} x^{- 5} d x = \frac{2}{3} (\frac{x^{- 4}}{- 4}) + C \\ = \frac{2}{3} (\frac{x^{- 4}}{- 4}) + C = \frac{x^{- 4}}{- 6} + C \end{array}$

Type 3:

$\begin{array}{l} \int (u + v) d x = \int u d x \pm \int v d x \\ u and v are functions in x \\ E x a m p l e 1 \\ \int 3 x^{2} + 2 x d x = \int 3 x^{2} d x + \int 2 x d x \\ = \frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} + C \\ = \frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} + C \\ = x^{3} + x^{2} + C \end{array}$

$\begin{array}{l} E x a m p l e 2 \\ \int (x + 2) (3 x + 1) d x = \int 3 x^{2} + 7 x + 2 d x \\ = \int 3 x^{2} d x + \int 7 x d x + \int 2 d x \\ = \frac{3 x^{3}}{3} + \frac{7 x^{2}}{2} + 2 x + C \\ = x^{3} + \frac{7 x^{2}}{2} + 2 x + C \end{array}$

$\begin{array}{l} E x a m p l e 3 \\ \int \frac{3 x^{3} + x^{2} - x}{x} d x = \int 3 x^{2} + x - 1 d x \\ = \int 3 x^{2} d x + \int x d x - \int 1 d x \\ = \frac{3 x^{3}}{3} + \frac{x^{2}}{2} - x + C \\ = x^{3} + \frac{x^{2}}{2} - x + C \end{array}$

Finding Equation Of A Curve From Its Gradient Function

Posted on April 22, 2020 by user

3.3 Finding Equation of a Curve from its Gradient Function

Example 1:
Find the equation of the curve that has the gradient function

$\frac{d y}{d x} = 2 x + 8$ and passes through the point (2, 3).

Solution:

$\begin{array}{l} y = \int (2 x + 8) \\ y = \frac{2 x^{2}}{2} + 8 x + C \end{array}$

y = x² + 8x + C

3 = 2² +8(2) + C (2, 3)

C = –17
Hence, the equation of the curve is
y = x² + 8x – 17

Example 2:

The gradient function of a curve is given by 2x – 4 and the curve has a minimum value of 3. Find the equation of the curve.

Solution:

At the point where a curve has a minimum value,

$\frac{d y}{d x} = 0$

2x – 4 = 0

x = 2

Therefore minimum point = (2, 3).

$\begin{array}{l} \frac{d y}{d x} = 2 x - 4 \\ y = \int (2 x - 4) d x \\ y = \frac{2 x^{2}}{2} - 4 x + C \\ y = x^{2} - 4 x + C \end{array}$

When x = 2, y = 3.

3 = 2² – 4(2) + c

c = 7

Hence, the equation of the curve is

y = x² – 4x + 7

Definite Integrals

Posted on April 22, 2020 by user

3.4a Definite Integral of f(x) from x=a to x=b

Example:

Evaluate each of the following.

$\begin{array}{l} (a) \int_{- 1}^{0} (3 x^{2} - 2 x + 5) d x \\ (b) \int_{0}^{2} {(2 x + 1)}^{3} d x \end{array}$

Solution:

$\begin{array}{l} (a) \int_{- 1}^{0} (3 x^{2} - 2 x + 5) d x \\ = {[\frac{3 x^{3}}{3} - \frac{2 x^{2}}{2} + 5 x]}_{- 1}^{0} \\ = {[x^{3} - x^{2} + 5 x]}_{- 1}^{0} \\ = 0 - [{(- 1)}^{3} - {(- 1)}^{2} + 5 (- 1)] \\ = 0 - (- 1 - 1 - 5) \\ = 7 \\ (b) \int_{0}^{2} {(2 x + 1)}^{3} d x \\ = {[\frac{{(2 x + 1)}^{4}}{4 (2)}]}_{0}^{2} \\ = {[\frac{{(2 x + 1)}^{4}}{8}]}_{0}^{2} \\ = [\frac{{(2 (2) + 1)}^{4}}{8}] - [\frac{{(2 (0) + 1)}^{4}}{8}] \\ = \frac{625}{8} - \frac{1}{8} \\ = 78 \end{array}$

Short Question 2 – 4

Posted on April 22, 2020 by user

Question 2:

Given that

$Given that \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c,$

find the values of m and n.

Solution:

$\begin{array}{l} \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c \\ \int 4 {(1 + x)}^{- 4} d x = m {(1 + x)}^{n} + c \\ \frac{4 {(1 + x)}^{- 3}}{- 3 (1)} + c = m {(1 + x)}^{n} + c \\ - \frac{4}{3} {(1 + x)}^{- 3} + c = m {(1 + x)}^{n} + c \\ m = - \frac{4}{3}, n = - 3 \end{array}$

Question 3:

$\begin{array}{l} Given \int_{- 1}^{2} 2 g (x) d x = 4, and \int_{- 1}^{2} [m x + 3 g (x)] d x = 15. \\ Find the value of constant m . \end{array}$

Solution:

$\begin{array}{l} \int_{- 1}^{2} [m x + 3 g (x)] d x = 15 \\ \int_{- 1}^{2} m x d x + \int_{- 1}^{2} 3 g (x) d x = 15 \\ {[\frac{m x^{2}}{2}]}_{- 1}^{2} + 3 \int_{- 1}^{2} g (x) d x = 15 \\ [\frac{m {(2)}^{2}}{2} - \frac{m {(- 1)}^{2}}{2}] + \frac{3}{2} \int_{- 1}^{2} 2 g (x) d x = 15 \\ 2 m - \frac{1}{2} m + \frac{3}{2} (4) = 15 \leftarrow given \int_{- 1}^{2} 2 g (x) d x = 4 \\ \frac{3}{2} m + 6 = 15 \\ \frac{3}{2} m = 9 \\ m = 9 \times \frac{2}{3} \\ m = 6 \end{array}$

Question 4:

$Given \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x), find \int_{1}^{2} g (x) d x .$

Solution:

$\begin{array}{l} Given \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x) \\ \int g (x) d x = \frac{2 x}{3 - x} \\ Thus, \\ \int_{1}^{2} g (x) d x = {[\frac{2 x}{3 - x}]}_{1}^{2} \\ = \frac{2 (2)}{3 - 2} - \frac{2 (1)}{3 - 1} \\ = 4 - 1 \\ = 3 \end{array}$

Long Question 6

Posted on April 22, 2020 by user

Question 6:
Diagram below shows part of the curve

$y = \frac{2}{{(3 x - 2)}^{2}}$ which passes through B (1, 2).

(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.

Solution:
(a)

$\begin{array}{l} y = \frac{2}{{(3 x - 2)}^{2}} = 2 {(3 x - 2)}^{- 2} \\ \frac{d y}{d x} = - 4 {(3 x - 2)}^{- 3} (3) \\ \frac{d y}{d x} = \frac{- 12}{{(3 x - 2)}^{3}} \\ \frac{d y}{d x} = \frac{- 12}{{(3 (1) - 2)}^{3}}, x = 1 \\ \frac{d y}{d x} = - 12 \\ y - 2 = - 12 (x - 1) \\ y - 2 = - 12 x + 12 \\ y = - 12 x + 14 \end{array}$

(b)(i)

$\begin{array}{l} Area = \int_{2}^{3} y d x \\ = \int_{2}^{3} \frac{2}{{(3 x - 2)}^{2}} d x = \int_{2}^{3} 2 {(3 x - 2)}^{- 2} d x \\ = {[\frac{2 {(3 x - 2)}^{- 1}}{- 1 (3)}]}_{2}^{3} \\ = {[- \frac{2}{3 (3 x - 2)}]}_{2}^{3} \\ = [- \frac{2}{3 [3 (3) - 2]}] - [- \frac{2}{3 [3 (2) - 2]}] \\ = - \frac{2}{21} + \frac{1}{6} \\ = \frac{1}{14} {unit}^{2} \end{array}$

(b)(ii)

$\begin{array}{l} Volume generated \\ = π \int y^{2} d x \\ = π \int_{2}^{3} \frac{4}{{(3 x - 2)}^{4}} d x = π \int_{2}^{3} 4 {(3 x - 2)}^{- 4} d x \\ = π {[\frac{4 {(3 x - 2)}^{- 3}}{- 3 (3)}]}_{2}^{3} = π {[- \frac{4}{9 {(3 x - 2)}^{3}}]}_{2}^{3} \\ = π [- \frac{4}{9 {[3 (3) - 2]}^{3}}] - [- \frac{4}{9 {[3 (2) - 2]}^{3}}] \\ = π (- \frac{4}{3087} + \frac{4}{576}) \\ = \frac{31}{5488} π {unit}^{3} \end{array}$

Gradient Of A Straight Line

Posted on April 22, 2020 by user

(B) Gradient of a Straight Line
If the points

$A (x_{1}, y_{1})$ and

$B (x_{2}, y_{2})$ lie on the straight line

$y = m x + c$ , then gradient of ,the straight line

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} o r \frac{y_{1} - y_{2}}{x_{1} - x_{2}}$

Steps To Draw The Line Of Best Fit

Posted on April 22, 2020 by user

Steps to draw a line of Best Fit
(i) Select suitable scales for the x-axis and the y-axis, make sure the points plotted accurately and the graph produced is large enough on the graph paper,
(ii) Mark the points correctly,
(iii) Use a long and transparent ruler to draw the line of best fit.

Step 1 : Select the suitable scale on x and y axis
(the graph produced must be more than 50% of the graph paper)

Step 2 : Mark the points correctly

Step 3 : Draw the Line of Best Fit

* Note

-the line passes through four points

-one point is above the line

-one point is below the line