SPM Practice 2 (Question 1 – 3)

Posted on April 22, 2020 by user

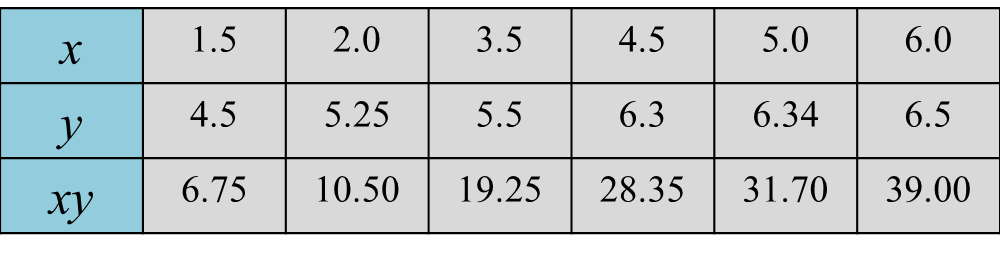
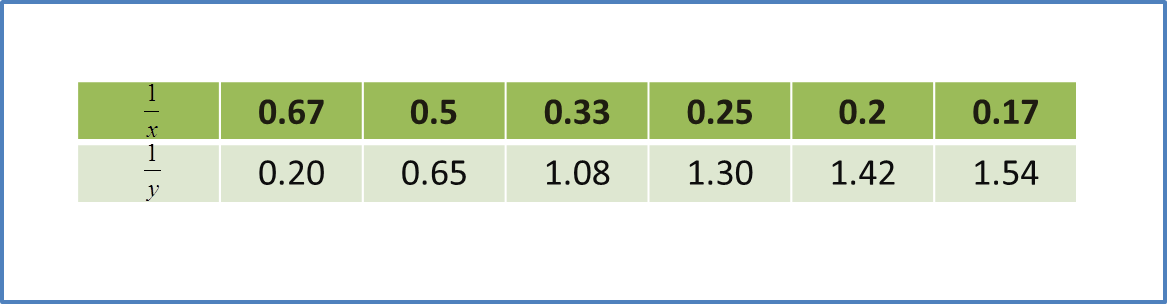
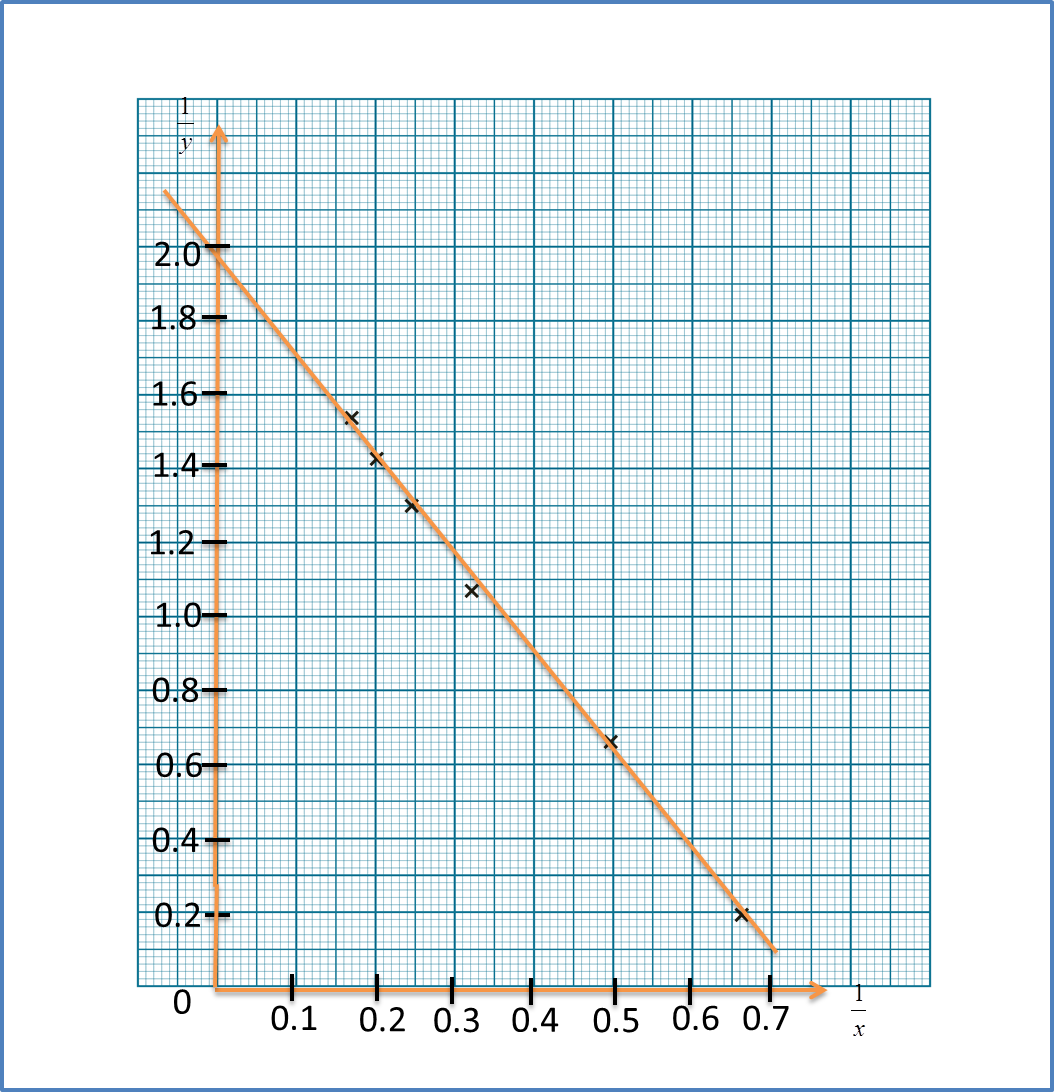
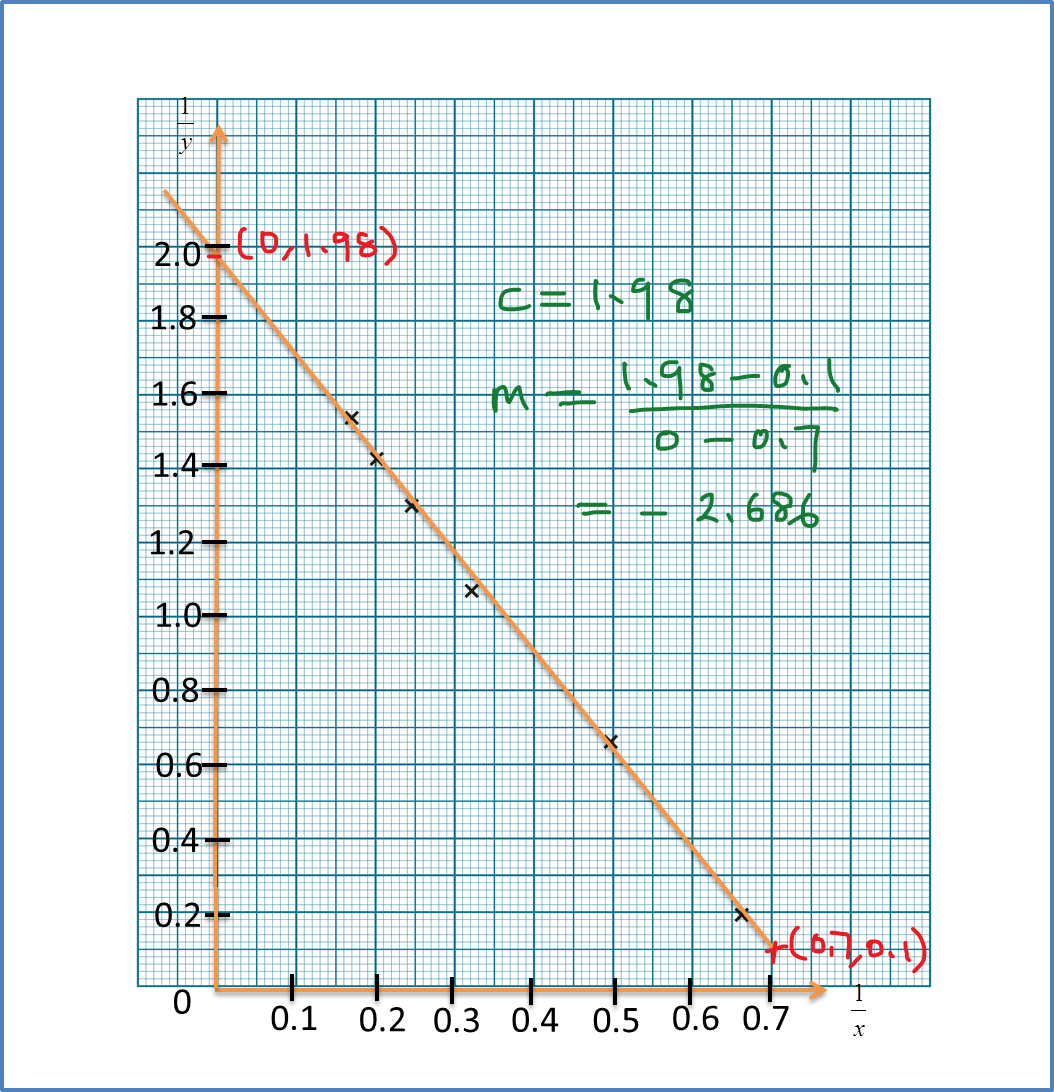
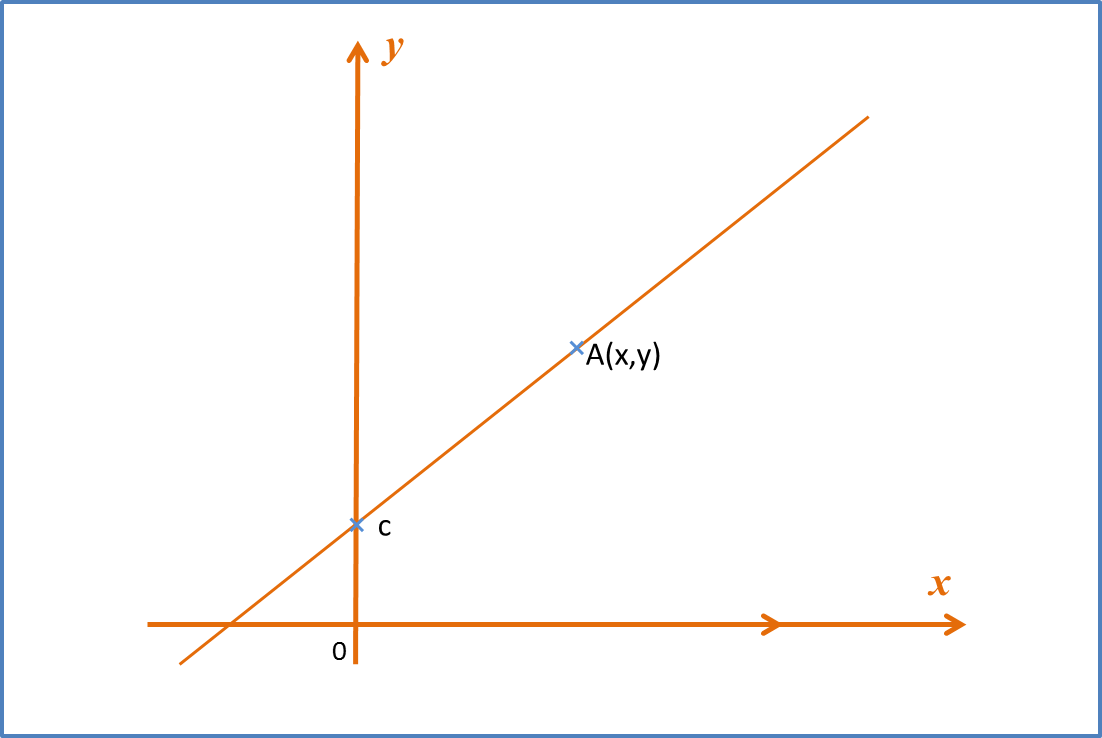
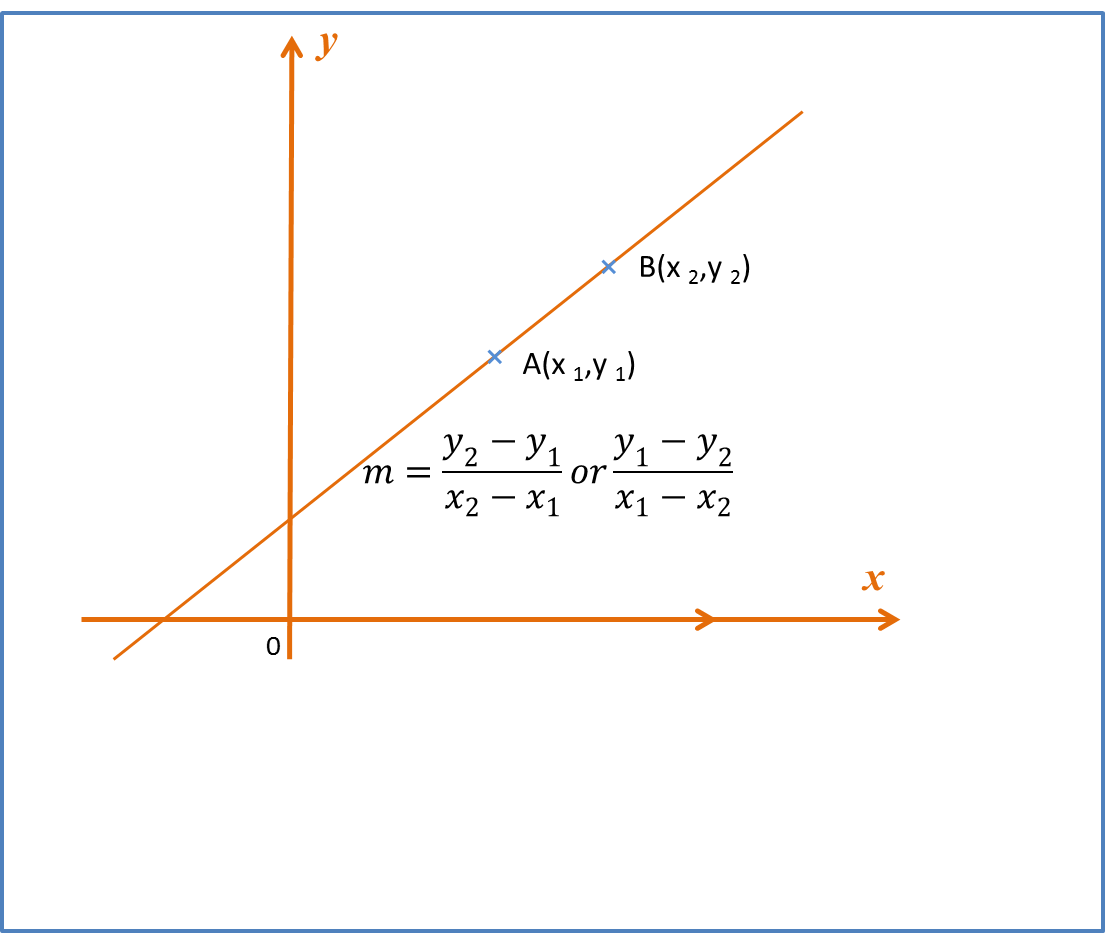
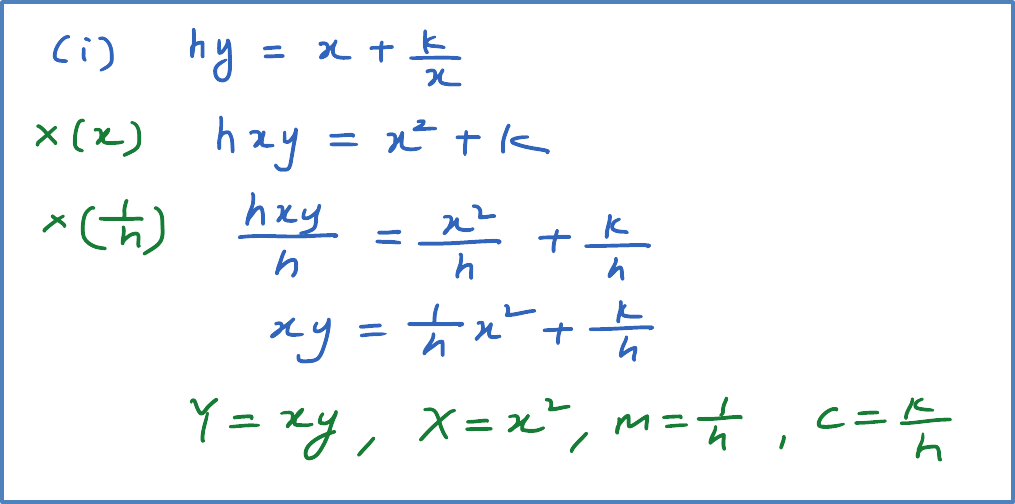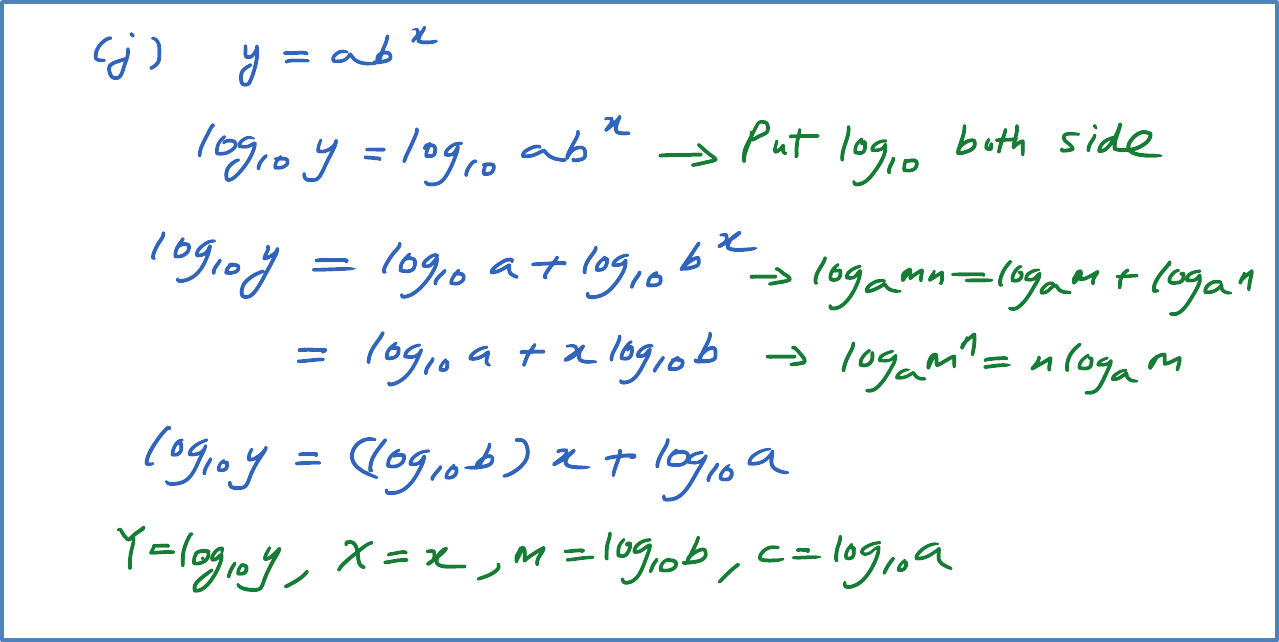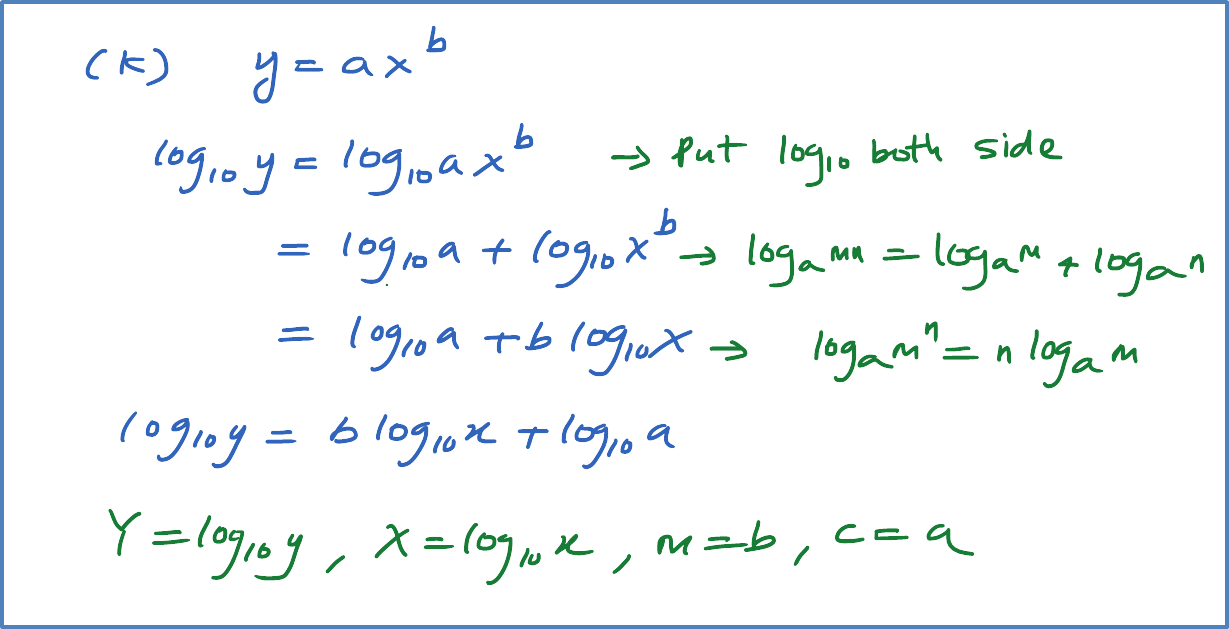Question 1:
Reduce non-linear relation, $y = p x^{n - 1}$ , where k and n are constants, to linear equation. State the gradient and vertical intercept for the linear equation obtained.
[Note : Reduce No-linear function to linear function]

Solution: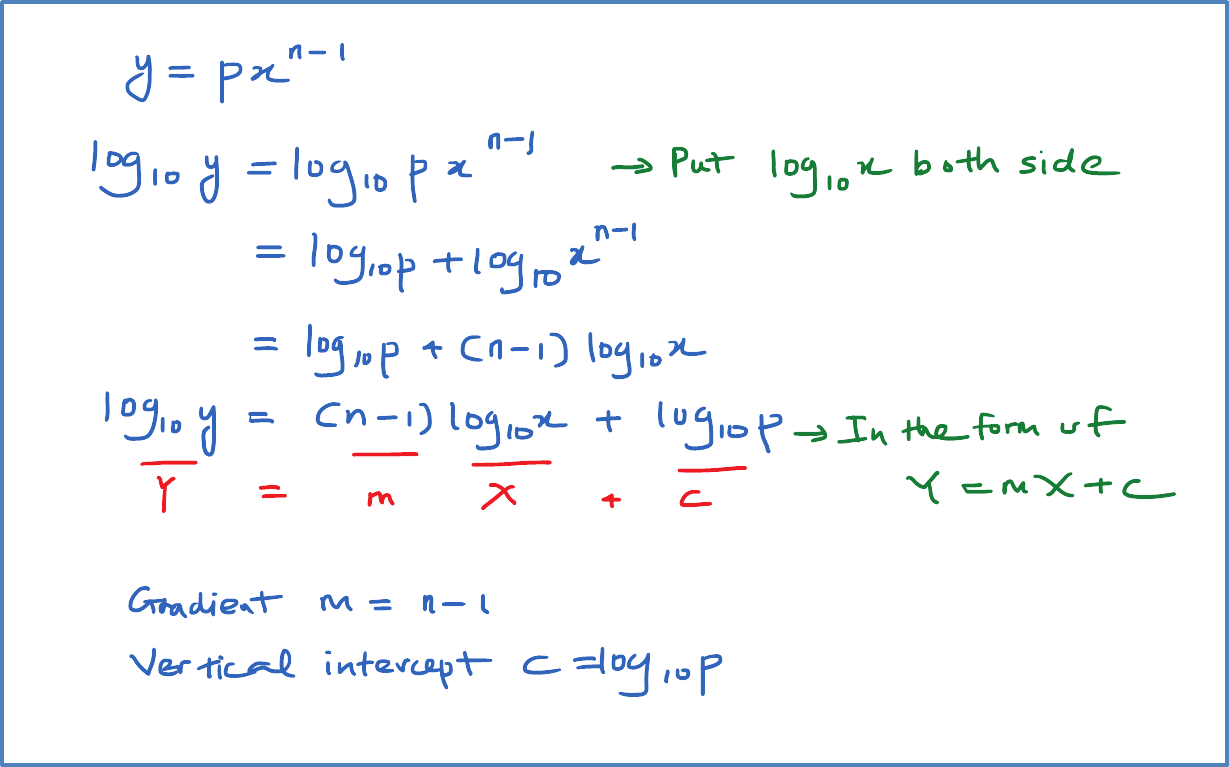

Question 2:
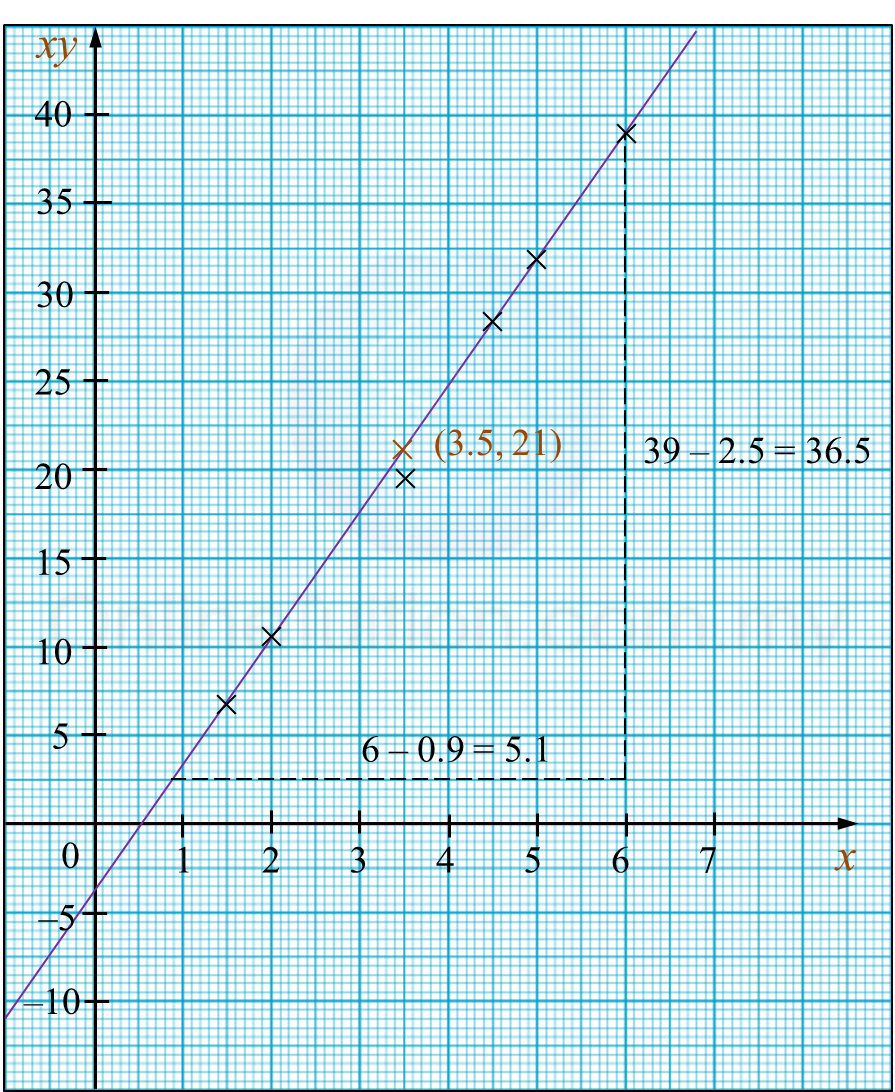
The diagram shows a line of best fit by plotting a graph of $y^{2}$ against $\s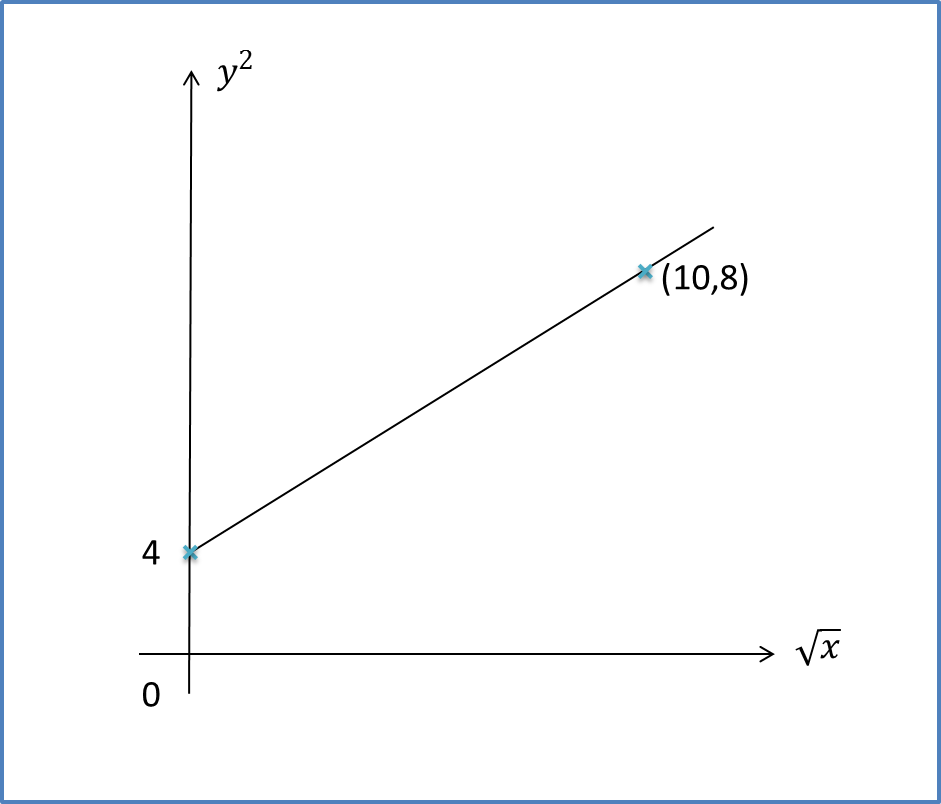qrt{x}$ .

Find the equation of the line of best fit.
Determine the value of
1. x when y = 4,
2. y when x = 25.

Solution:

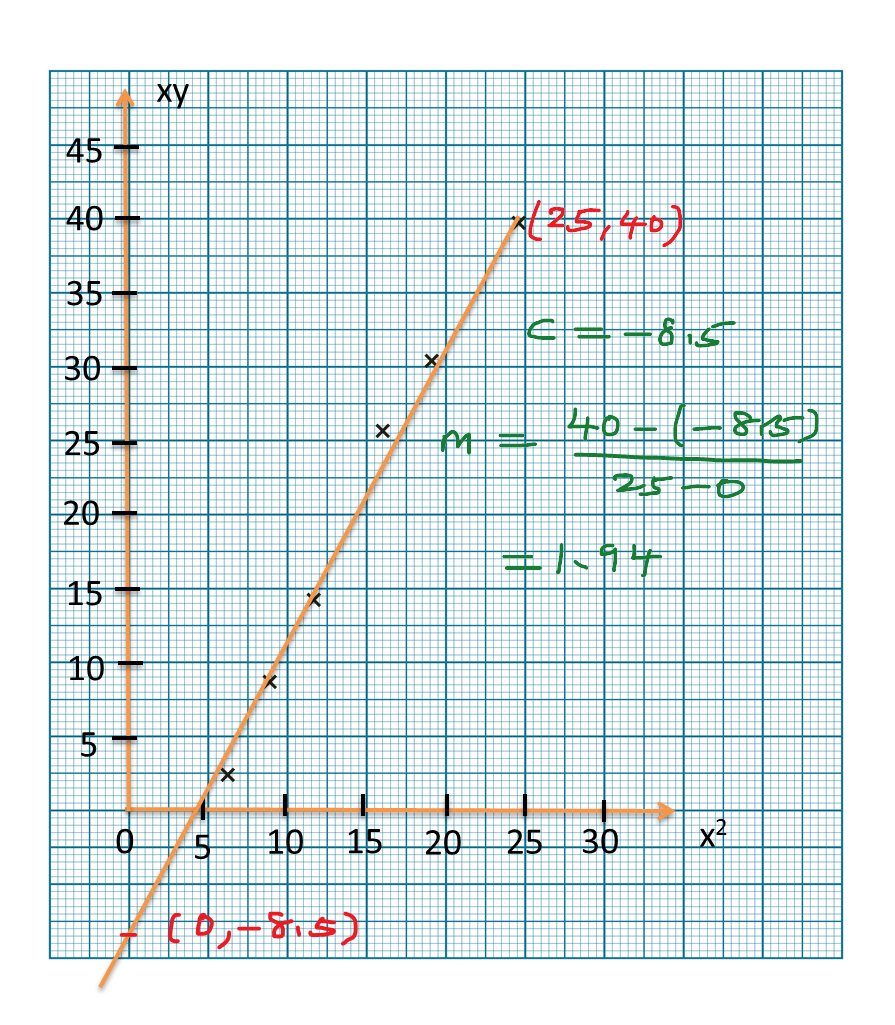
Question 3:
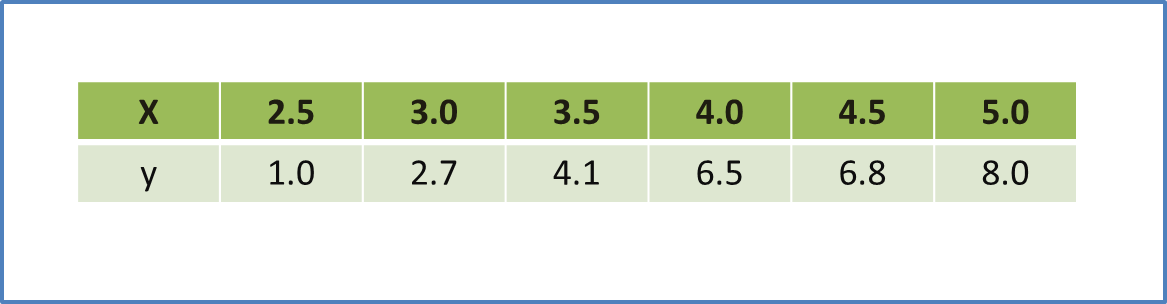
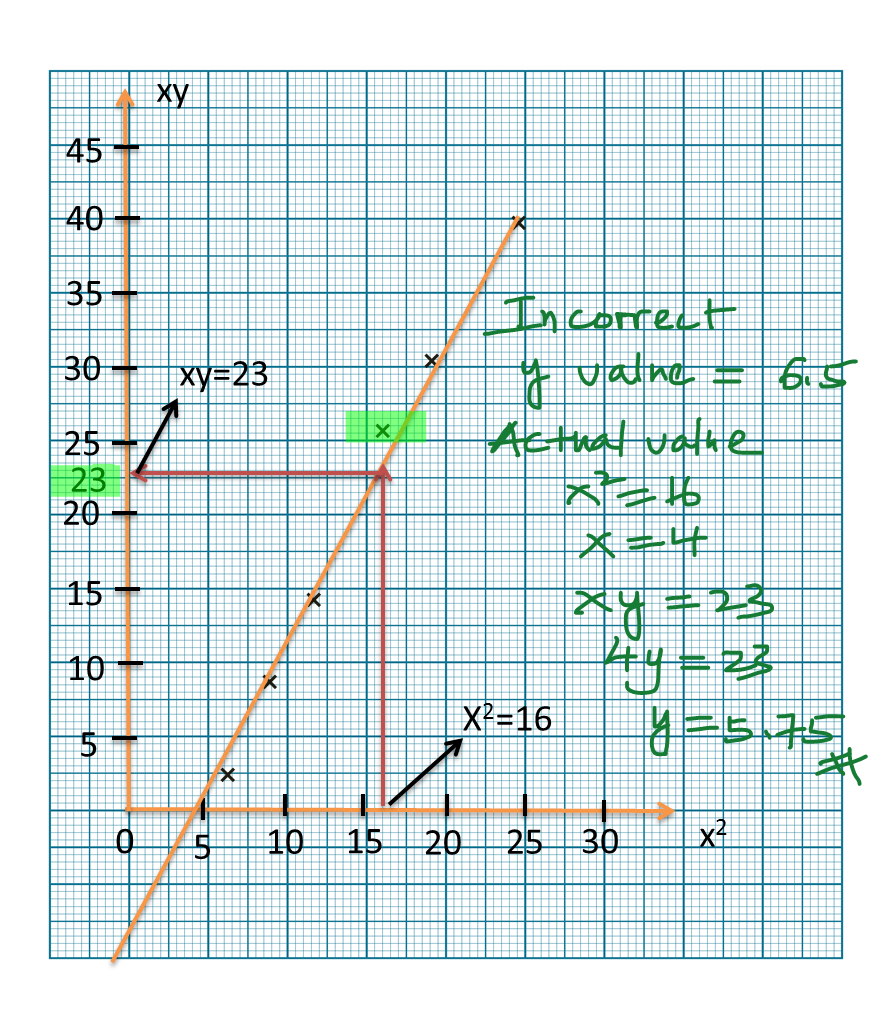
The diagram shows part of the straight line graph obtained by plotting $\sqrt{y}$ against $x^{2}$ .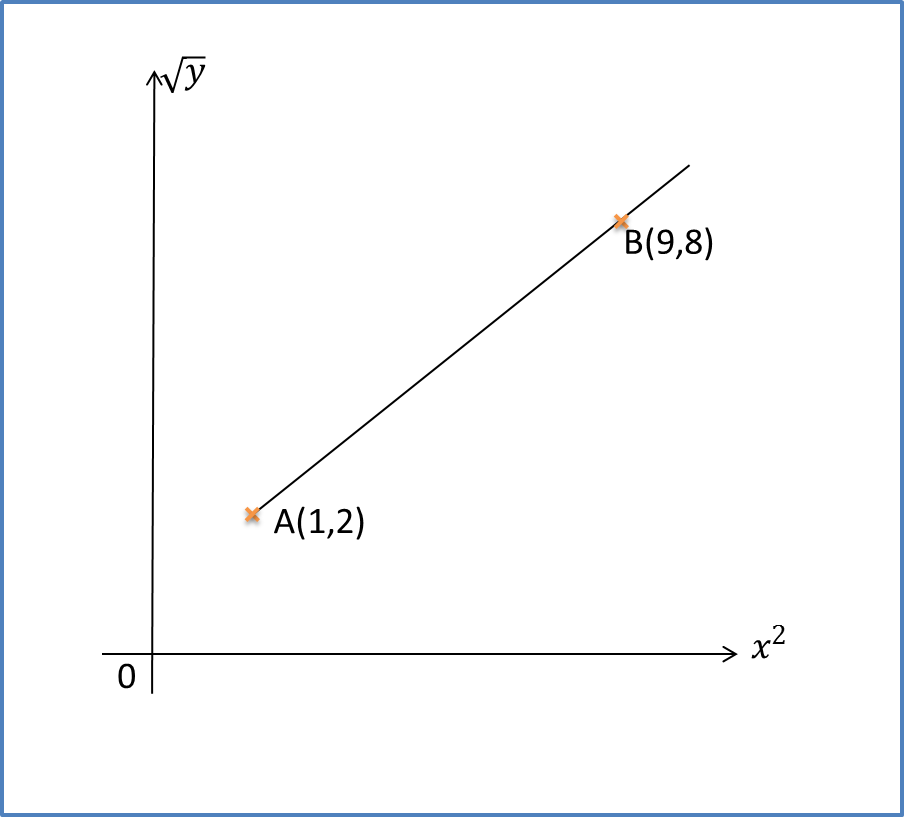

Express y in terms of x.

Solution:

SPM Practice 3 (Linear Law) – Question 1

Posted on April 22, 2020 by user

Question 1 (10 marks):
Use a graph to answer this question.
Table 1 shows the values of two variables, x and y, obtained from an experiment.
The variables x and y are related by the equation

$y - \sqrt{h} = \frac{h k}{x}$ , where h and k are constants.

(a) Plot xy against x, using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the xy-axis.
Hence, draw the line of best fit.

(b) Using the graph in 9(a), find
(i) the value of h and of k,
(ii) the correct value of y if one of the values of y has been wrongly recorded during the experiment.

Solution:
(a)

(b)

$\begin{array}{l} y - \sqrt{h} = \frac{h k}{x} \\ x y - \sqrt{h} x = h k \\ x y = \sqrt{h} x + h k \\ Y = m X + C \\ Y = x y, m = \sqrt{h}, C = h k \end{array}$

(b)(i)

$\begin{array}{l} m = \frac{36.5}{5.1} \\ \sqrt{h} = \frac{36.5}{5.1} \\ \sqrt{h} = 7.157 \\ h = 51.22 \\ C = - 4 \\ h k = - 4 \\ k = \frac{- 4}{h} \\ k = - \frac{4}{51.22} \\ k = - 0.0781 \end{array}$

(b)(ii)

$\begin{array}{l} x y = 21 \\ 3.5 y = 21 \\ y = \frac{21}{3.5} = 6.0 \\ Correct value of y is 6 .0 . \end{array}$

Tips To Reduce Non-Linear Function To Linear Function

Posted on April 22, 2020 by user

Tips:
(1) The equation must have one constant (without x and y).
(2) X and Y cannot have constant, but can have the variables (for example x and y).
(3) m and c can only have the constant (for example a and b), cannot have the variables x and y.

Examples
(1)
X and Y cannot have constant, but can have the variables (for example x and y)

(2)
m and c can only have the constant (for example a and b), cannot have the variables x and y

SPM Practice 2 (Linear Law) – Question 4

Posted on April 22, 2020 by user

Question 4
The table below shows the corresponding values of two variables, x and y, that are related by the equation

$y = q x + \frac{p}{q x}$ , where p and q are constants.

One of the values of y is incorrectly recorded.
(a) Using scale of 2 cm to 5 units on the both axis, plot the graph of xy against

$x^{2}$ . Hence, draw the line of best fit

(b) Use your graph in (a) to answer the following questions:
(i) State the values of y which is incorrectly recorded and determine its actual value.
(ii) Find the value of p and of q.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

Steps to draw line of best fit - Click here

(b) (i) State the values of y which is incorrectly recorded and determine its actual value.

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required

Distance Between Two Points

Posted on April 22, 2020 by user

Distance between point $A (x_{1}, y_{1})$ and point is $B (x_{2}, y_{2})$ given by

$\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

Reduce Non-Linear Function To Linear Function – Examples (G) To (L)

Posted on April 22, 2020 by user

Examples:
Reduce each of the following equations to the linear form. Hence, state the gradient and the Y-intercept of the linear equations in terms of a and b.

(g)

$k x^{2} + t y^{2} = x$

(h)

$y = \frac{x}{p + q x}$

(i)

$h y = x + \frac{k}{x}$

(j)

$y = a b^{x}$

(k)

$y = a x^{b}$

(l)

$y = a b^{x + 1}$

[Note :
X and Y cannot have constant, but can have the variables (for example x and y)
m and c can only have the constant (for example a and b), cannot have the variables x and y]

Solution:

SPM Practice 3 (Linear Law) – Question 3

Posted on April 22, 2020 by user

Question 3
The table below shows the values of two variables, x and y, obtained from an experiment. The variables x and y are related by the equation

$\frac{a}{y} = \frac{b}{x} + 1$ , where k and p are constants.

(a) Based on the table above, construct a table for the values of

$\frac{1}{x}$ and

$\frac{1}{y}$ . Plot

$\frac{1}{y}$ against

$\frac{1}{x}$ , using a scale of 2 cm to 0.1 unit on the

$\frac{1}{x}$ - axis and 2 cm to 0.2 unit on the

$\frac{1}{y}$ - axis. Hence, draw the line of best fit.
(b) Use the graph from (b) to find the value of
(i) a,
(ii) b.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

Steps to draw line of best fit - Click here

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required

Revise of Important Concept – Straight Line

Posted on April 22, 2020 by user

(A) Equation of a straight Line

An equation of straight line is given by y = mx + c.
• The variables x and y are linearly related
• The term c is known as y-intercept. It represents the y value where the line cuts the y-axis
• The term m is the gradient of the straight line and its value is constant

(B) Gradient of a Straight Line
If the points

$A (x_{1}, y_{1})$ and

$B (x_{2}, y_{2})$ lie on the straight line

$y = m x + c$ , then gradient of ,the straight line

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} o r \frac{y_{1} - y_{2}}{x_{1} - x_{2}}$

(C) Mid Point

Mid Point AB is given by

$M = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

(D) Distance Between Two Points
Distance between point

$A (x_{1}, y_{1})$ and point is

$B (x_{2}, y_{2})$ given by

$\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

Linear Versus Non-Linear Function

Posted on April 22, 2020 by user

Linear Function (Straight Line)

Examples :
(a) y = 3x + 5
(b) 3y + 2x - 7 = 0

Non-Linear Function

Examples :
(a)

$y = a x^{3} + b x^{2}$

(b)

$y = a x + \frac{b}{x}$

(c)

$y = a b^{x}$

(d)

$y = \frac{x}{p + q x}$

Equations Of Line Of Best Fit

Posted on April 22, 2020 by user

A set of two variables are related non linearly can be converted to a linear equation. The line of best fit can be written in the form

Y = mX + c

where
X and Y are in terms of x and/or y
m is the gradient,
c is the Y-intercept

Recall: To find equation of straight line
(1) Equation of a straight line if gradient (m) and one points

$(x_{1}, y_{1})$ are given:

$Y - y_{1} = m (X - x_{1})$
(2) Equation of a straight line if gradient (m) and y-intercept (c) are given:

$Y = m X + c$