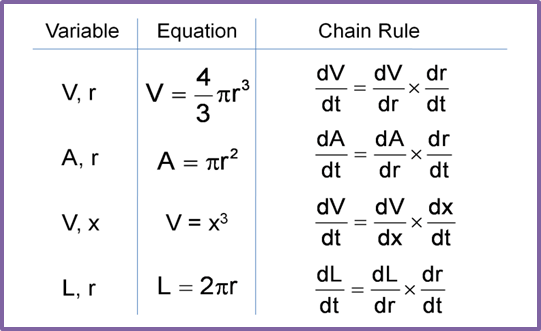
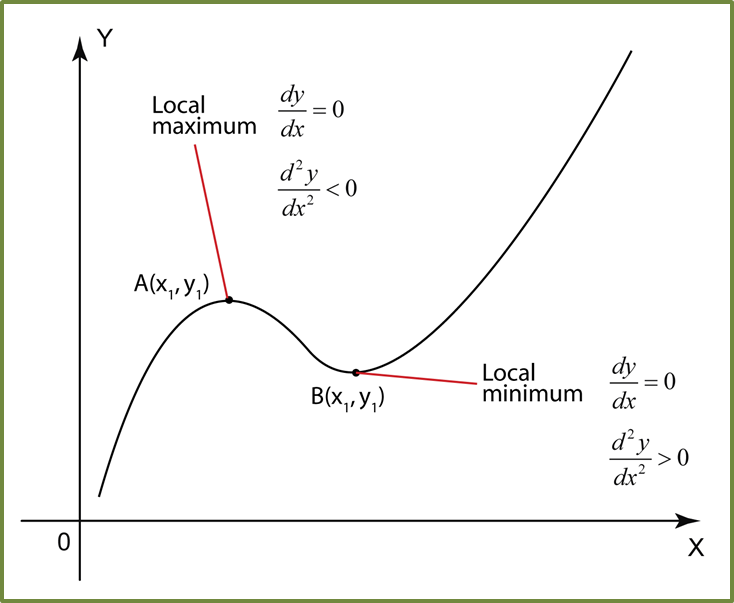
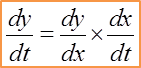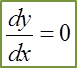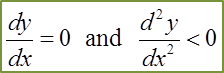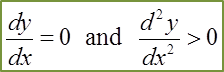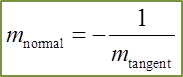Question 14:
Hence, find the value of x which satisfies the equation
Solution:
Given y = x (6 – x), express
in terms of x in the simplest form.
Hence, find the value of x which satisfies the equation
Solution:
Question 15:
Solution:
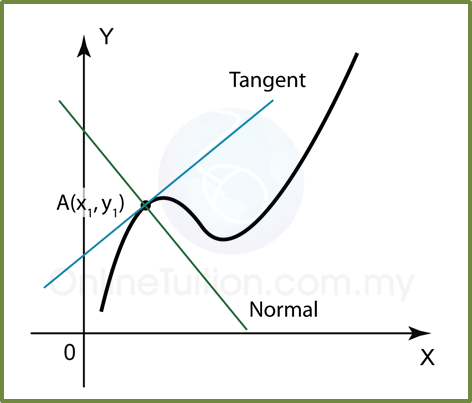
Find the coordinates of the point on the curve, y = (4x – 5)2 such that the gradient of the normal to the curve is
.
Solution:
y = (4x – 5)2
= 2(4x – 5).4 = 32x – 40
Given the gradient of the normal is 1/8, therefore the gradient of the tangent is –8.
= –8
32x – 40 = –8
32x = 32
x = 1
y = (4(1) – 5)2= 1
Hence, the coordinates of the point on the curve, y = (4x – 5)2 is (1, 1).
Question 16:
Solution:
y + 2x –1 = 0, y = –2x + 1, gradient of the straight line = –2
A curve has a gradient function of kx2 – 7x, where k is a constant. The tangent to the curve at the point (1, 4) is parallel to the straight line y + 2x–1 = 0. Find the value of k.
Solution:
Gradient function of kx2– 7x is parallel to the straight line y + 2x–1 = 0
= kx2– 7x
y + 2x –1 = 0, y = –2x + 1, gradient of the straight line = –2
Therefore kx2– 7x = –2
At the point (1, 4),
k(1)2 – 7(1) = –2
k – 7 = –2
k = 5