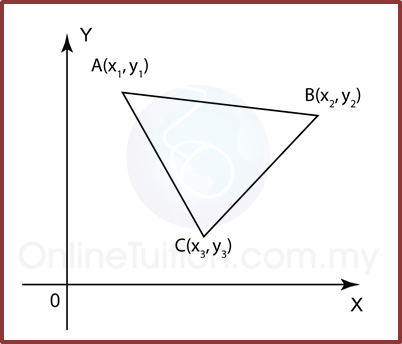
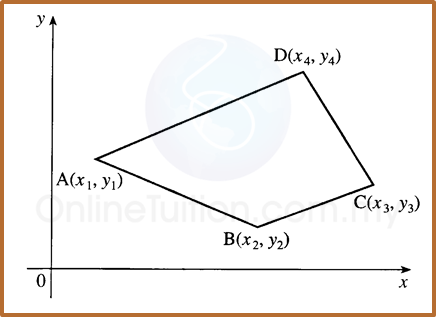
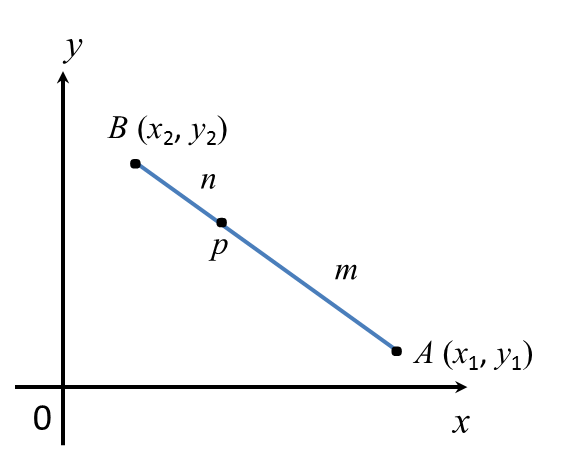
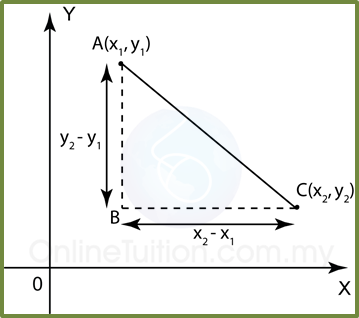
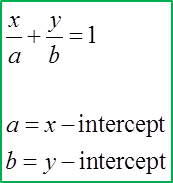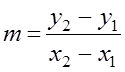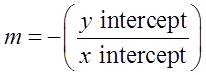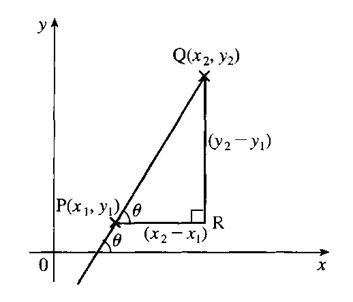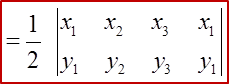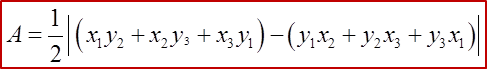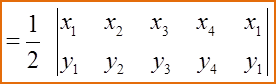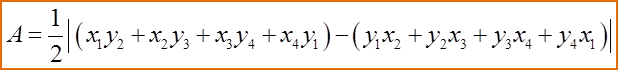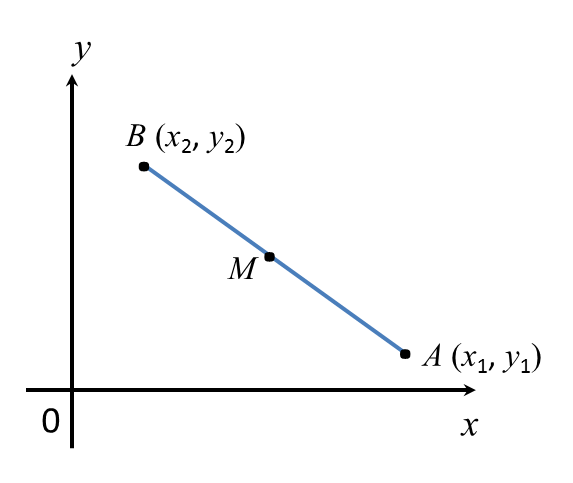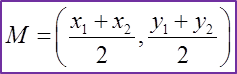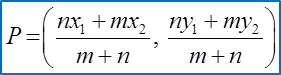Question 3:
Solution:
The equation of the straight lines CD and EF are 5x + y – 4 = 0 and
x7−yh=1
. If CD and EF are parallel, find the value of h.
Solution:
Two parallel lines have same gradient.
5x + y – 4 = 0
y = –5x + 4, mCD = –5
For the straight line EF,
x7−yh=1mEF=−(y-interceptx-intercept)=−(−h7)=h7mCD=mEF−5=h7h=−35
Question 4:
Solution:
Given y-intercept of the straight line x5+yp=1 is 3,∴
The straight line
x5+yp=1
has a y-intercept of 3 and is parallel to the straight line y + qx = 0. Determine the value of p and of q.
Solution:
Given y-intercept of the straight line x5+yp=1 is 3,∴
Question 5:
Solution:
Hence, the two straight lines are perpendicular to each other.
The equations of two straight lines
y = 4x + 21. Determine whether the lines are perpendicular to each other.
Solution:
Hence, the two straight lines are perpendicular to each other.