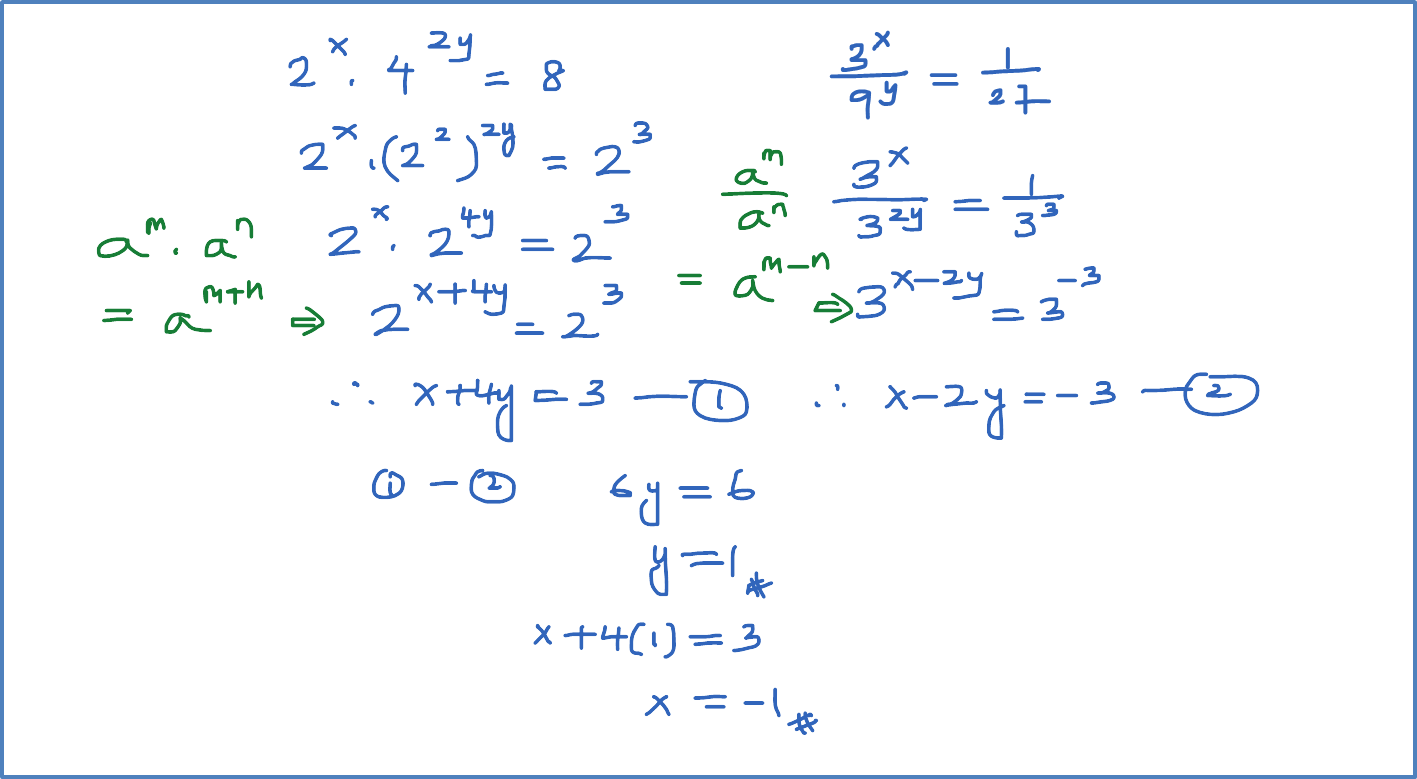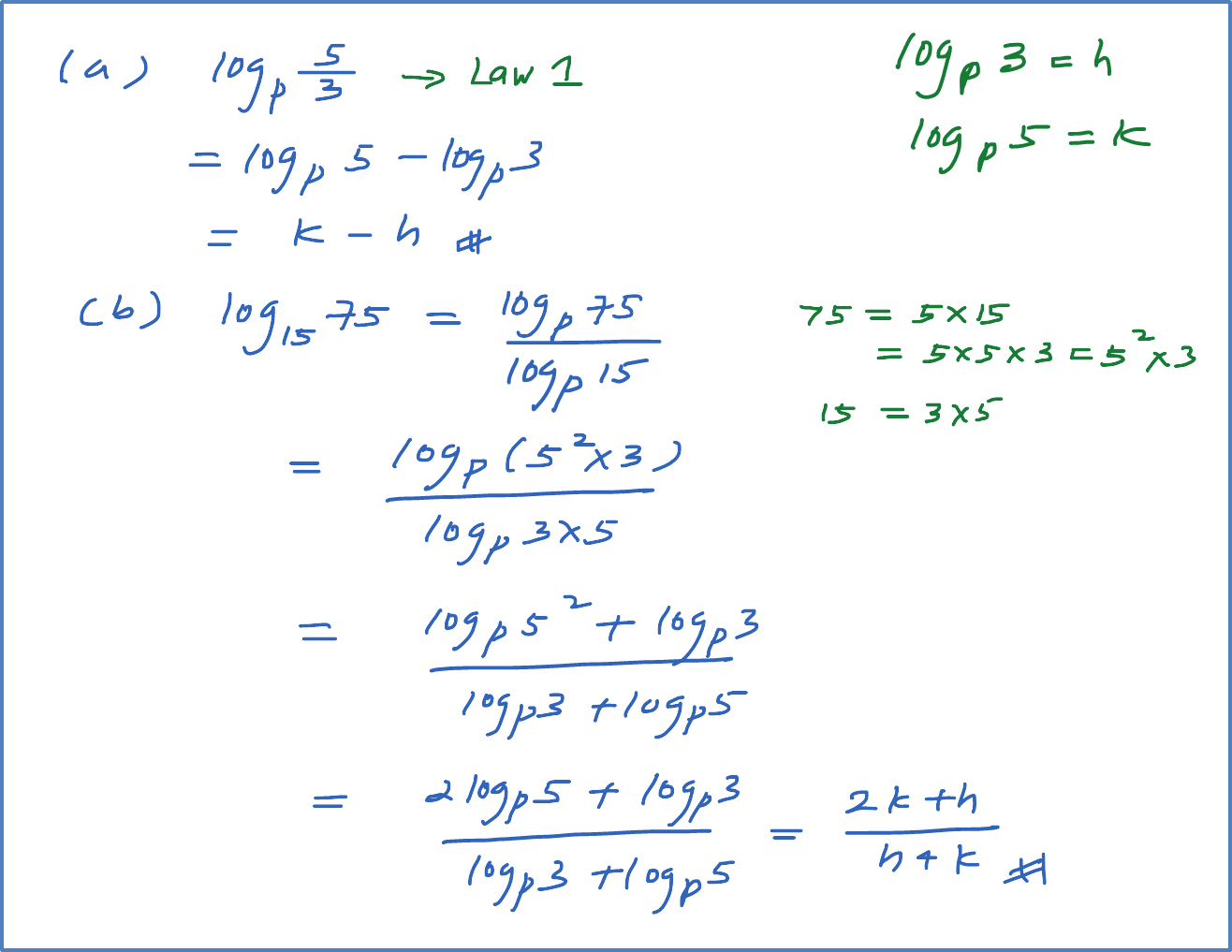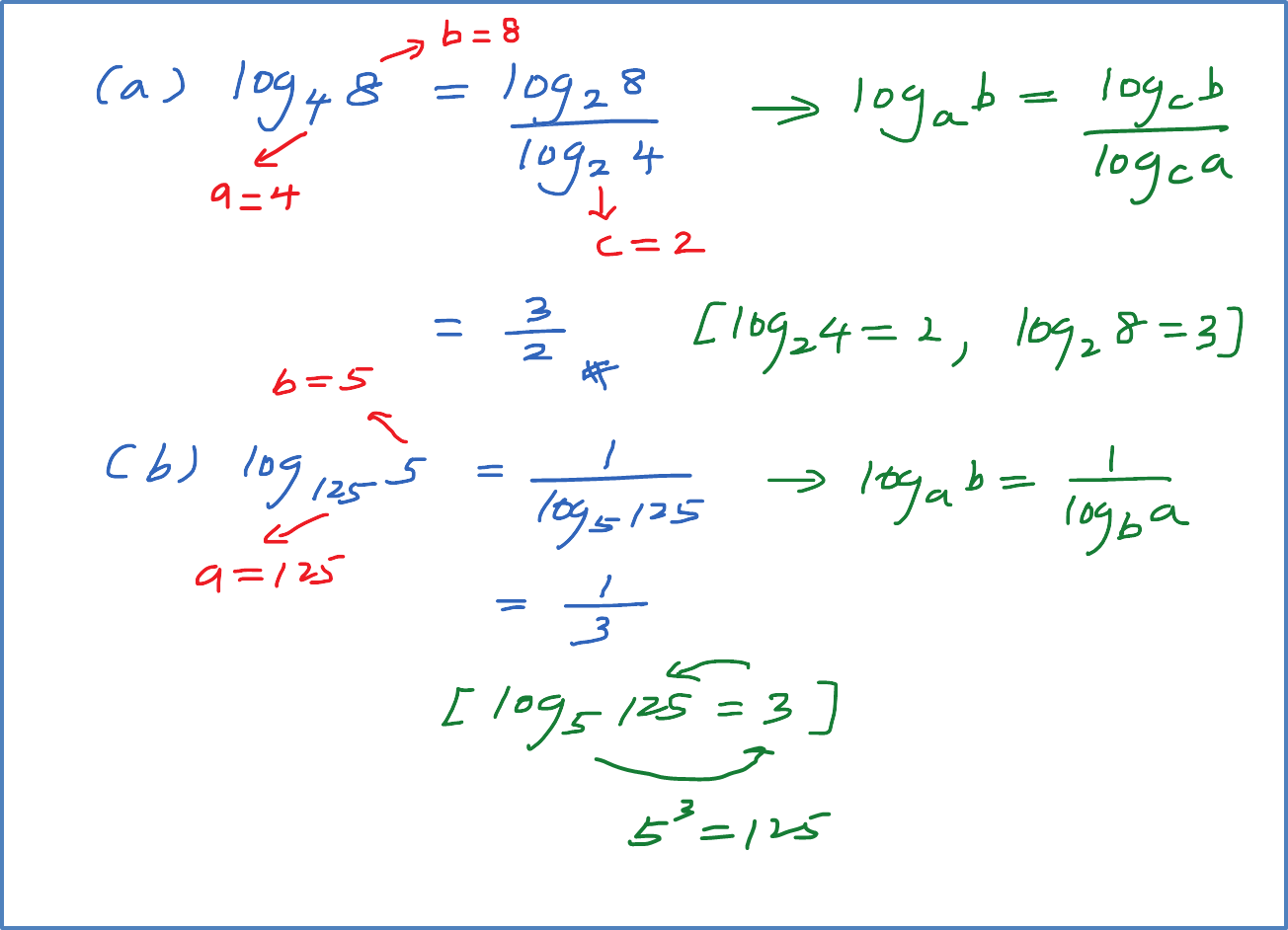Example 3 (Index Equation - Equal Base)
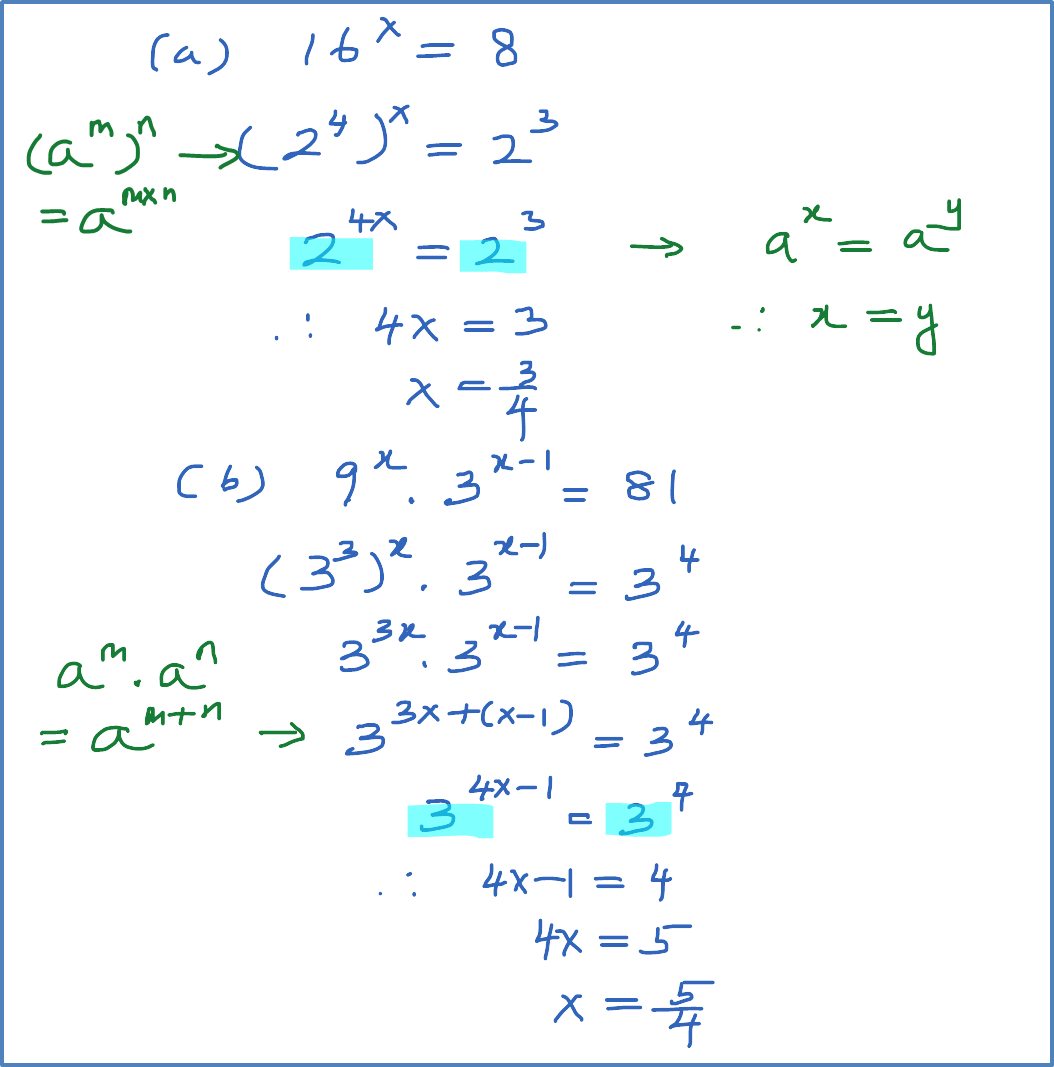
Solve each of the following.
(a) 27(813x)=1
(b) √81n+2=13n27n−1
(c) 8x−1=4√2x+3



Solve each of the following.
(a) 27(813x)=1
(b) √81n+2=13n27n−1
(c) 8x−1=4√2x+3