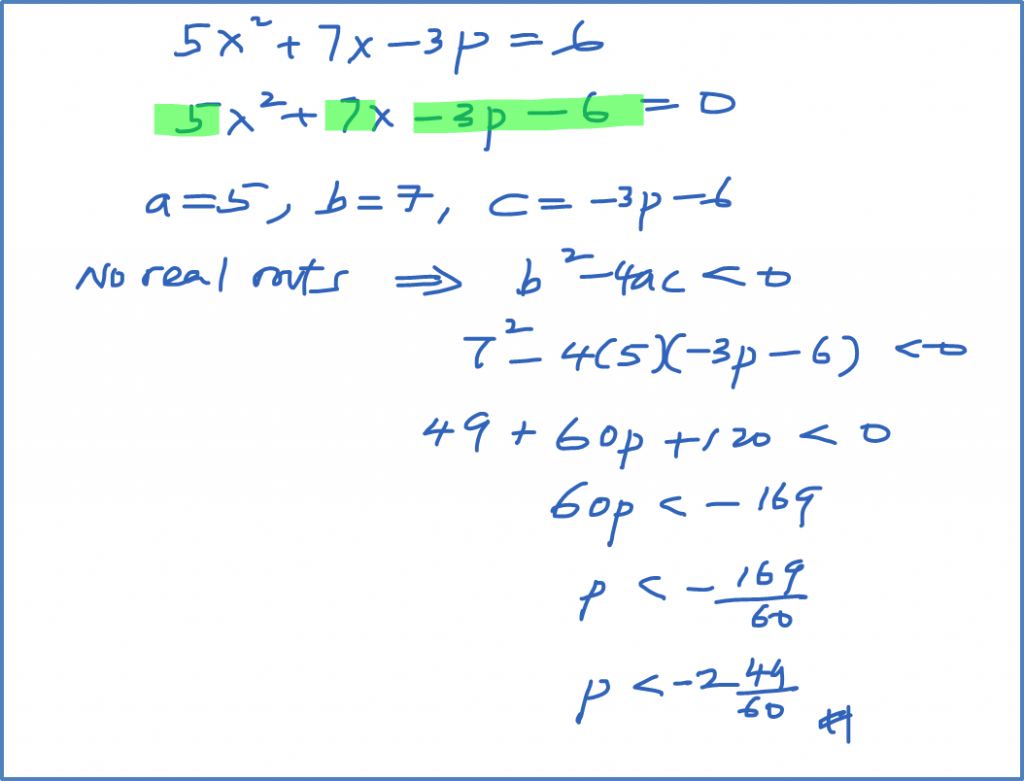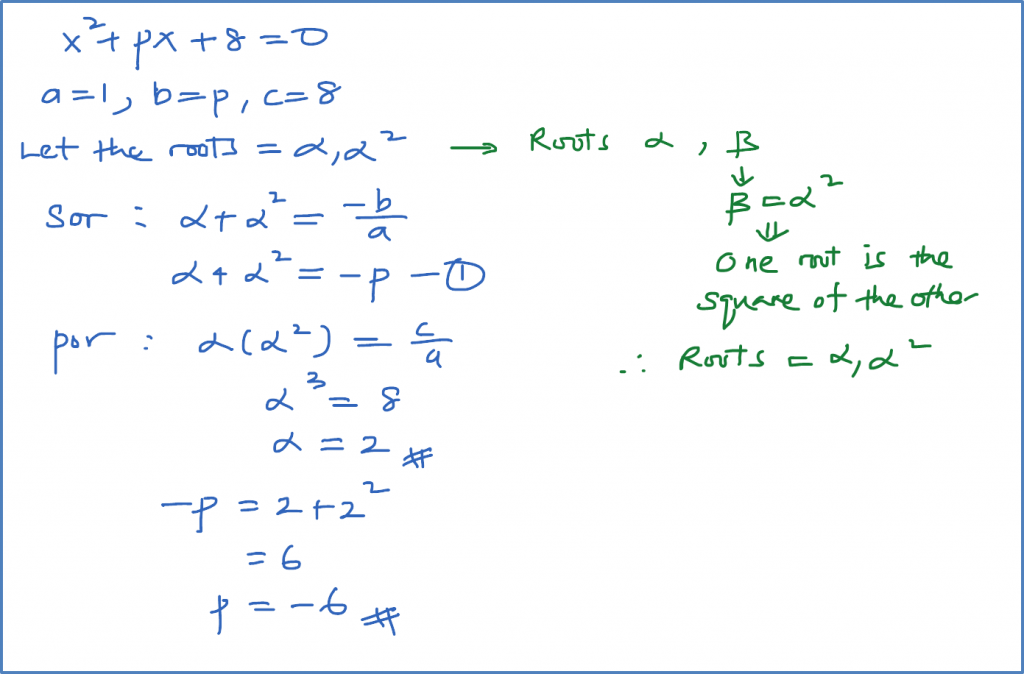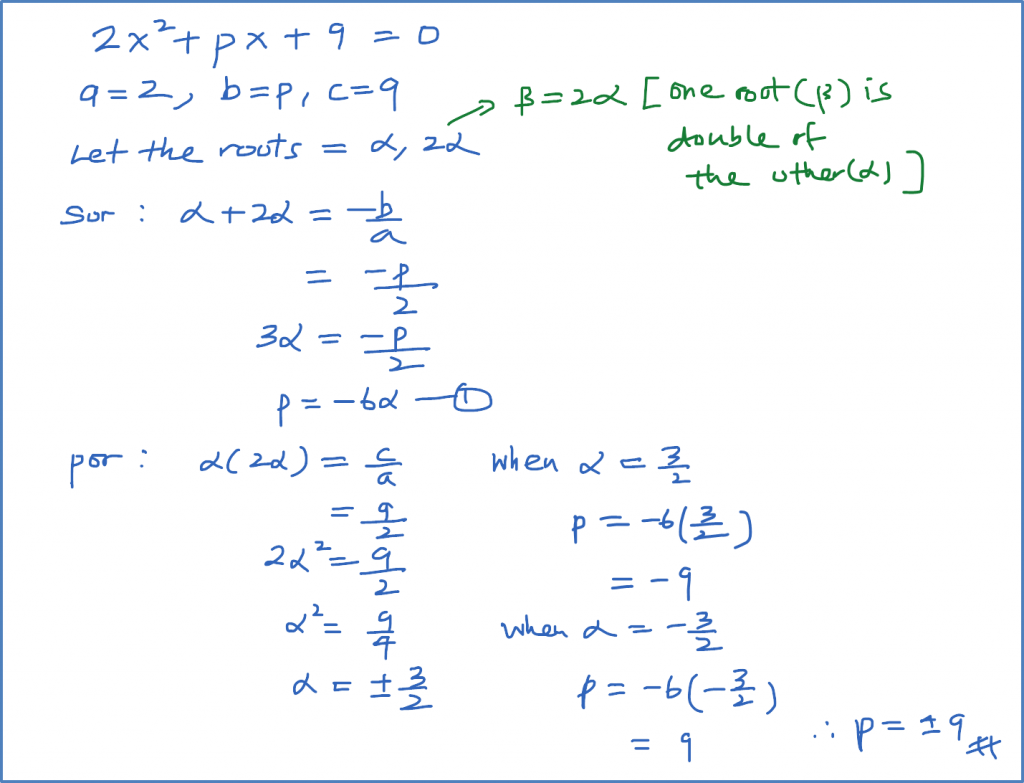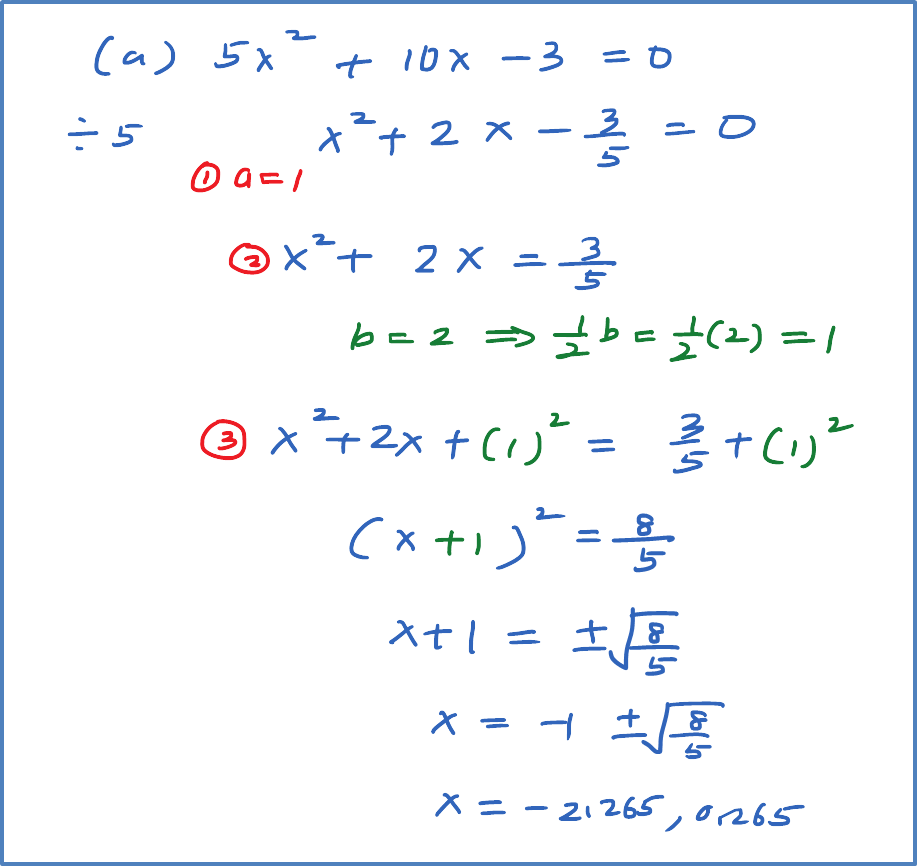Question 11:
The quadratic equation x2−4x−1=2p(x−5) , where p is a constant, has two equal roots. Calculate the possible values of p.
Solution:

The quadratic equation x2−4x−1=2p(x−5) , where p is a constant, has two equal roots. Calculate the possible values of p.
Solution:

Question 12:
Find the range of values of k for which the equation x2−2kx+k2+5k−6=0 has no real roots.
Solution:

Find the range of values of k for which the equation x2−2kx+k2+5k−6=0 has no real roots.
Solution:

Question 13:
Find the range of values of p for which the equation 5x2+7x−3p=6 has no real roots.
Solution:
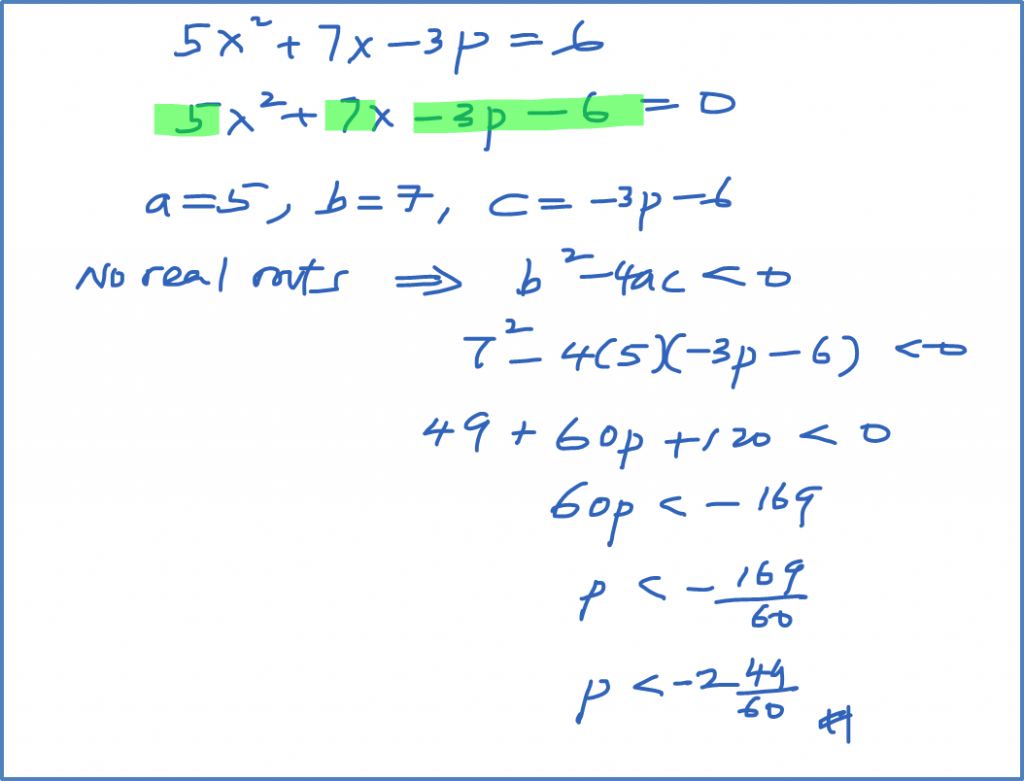
Find the range of values of p for which the equation 5x2+7x−3p=6 has no real roots.
Solution: