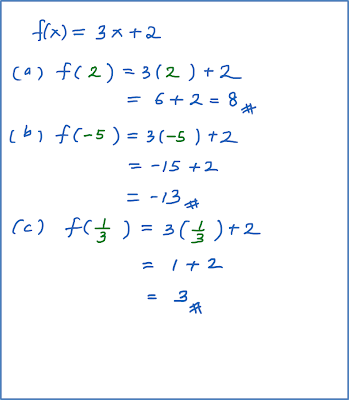Composite Function (Comparison Method) Example 1

Posted on April 18, 2020 by user

Example 1
Given

$f : x \mapsto h x + k, g : x \mapsto {(x + 1)}^{2} + 4$ and

$f g : x \mapsto 2 {(x + 1)}^{2} + 5.$ Find
(a) the value of g²(2),
(b) the value of h and of k.

Example 3

Posted on April 18, 2020 by user

Example 3

If

$f : x \mapsto 2 x + 1$ and

$g : x \mapsto \frac{5}{x}, x \neq 0$ . Find the composite functions gf , fg and the value of gf(4).

Example 2

Posted on April 18, 2020 by user

Given $f : x \mapsto 1 - x$ and $g : x \mapsto p x^{2} + q$ . If the composite function gf is defined by $g f : x \mapsto 3 x^{2} - 6 x + 5$ , find

the value of p and of q,
the value of $g^{2} (- 1)$ .

Example 2

Posted on April 18, 2020 by user

Example 2

Functions f and g are defined by

$f : x \mapsto x - 1$ and

$g : x \mapsto \frac{3 - x}{x + 4}$ . Find
(a) the value of gf(3),
(b) the value of fg(-1 ),
(c) the composite functions fg,
(d) the composite functions gf,
(e) the composite functions g²,
(f) the composite functions f².

Example 1

Posted on April 18, 2020 by user

If f : x → x + 5 and g : x → x² +2x + 3, find

the value of gf (2),
the value of fg (2 ),
the composite functions fg,
the composite functions gf,
the composite functions g² ,
the composite functions f².

correction for part (c)

$\begin{array}{l} f g (x) = f (x^{2} + 2 x + 3) \\ = (x^{2} + 2 x + 3) + 5 \\ = x^{2} + 2 x + 3 + 5 \\ = x^{2} + 2 x + 8 \end{array}$

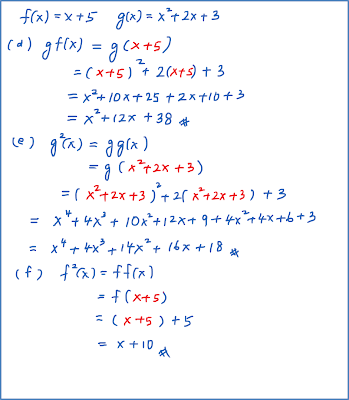
1.3a Composite Function

Posted on April 18, 2020 by user

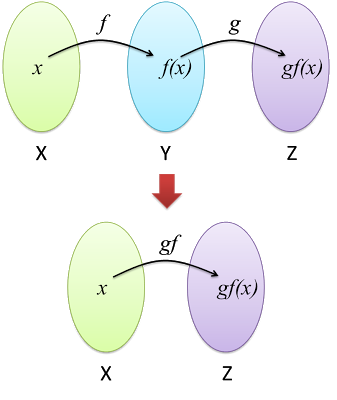
Composite Function

If function

$f : X \mapsto Y$ ,
and function

$g : Y \mapsto Z$ ,
hence, composite function

$g f : X \mapsto Z$

Example:
If,

$f : x \mapsto 2 x + 5$ and

$g : x \mapsto x^{2} - 1$ , find

$g f (2)$

Answer:
$\begin{array}{l} f (x) = 2 x + 5 \\ f (2) = 2 (2) + 5 = 9 \end{array}$

$g f (2) = g [f (2)] = g (9)$

$\begin{array}{l} g (x) = x^{2} - 1 \\ g f (2) = g (9) = 9^{2} - 1 = 80 \end{array}$

Online Video Lessons

Youtube Video Lesson 1
Youtube Video Lesson 2
Youtube Video Lesson 3

Example 4 and 5

Posted on April 18, 2020 by user

Example 4
Given the function

$f : x \mapsto 3 x + 2$ , find the value of
(a)

$f (2)$
(b)

$f (- 5)$
(c)

$f (\frac{1}{3})$

Example 5
If

$f (x) = x^{2} + 3 x + 2$ , express each of the following in terms of x:
(a)

$f (2 x)$
(b)

$f (3 x + 1)$
(c)

$f (x^{2})$

Example 2 and 3

Posted on April 18, 2020 by user

Example 2

Function f is defined as

$f : x \to \frac{5}{2 x - 1}, x \neq k$

Find the value of k.

Example 3

Given

$g : x \to \frac{3 x - 5}{2 x + 7}$

Function g is defined for all values of x except x = a. Find the value of a.

Domain, Range, Objects, Images and Absolute Value Functions

Posted on April 18, 2020 by user

(B) Domain, Range, Objects and Images of a Function

Example:

The arrow diagram above represents the function f : x → 2x² – 5. State
(a) the domain,
(b) the range,
(c) the image of –2,
(d) the objects of
(i) –3,
(ii) –5.

Solution:
(a) Domain = {–2, –1, 0, 1, 2}.
(b) Range = {–5, –3, 3}.
(c) The image of –2 is 3.
(d) (i) The objects of –3 are 1 and –1.
(d) (ii) The objects of –5 is 0.

(C) Absolute Value Functions

1. Symbol | | is read as ‘the modulus’ of a number. In general, the modulus of x, that is | x |, is defined as

$| x | = {\begin{cases} x if x \geq 0 \\ - x if x < 0 \end{cases}$

2. In other words, modulus of a number always positive.
3. The absolute value function | f(x) | is defined by

$| f (x) | = {\begin{cases} f (x) if f (x) \geq 0 \\ - f (x) if f (x) < 0 \end{cases}$

Example:
Given function f : x → |x + 2|.
(a) Find the image of –4, –3, 0 and 2.
(b) Sketch the graph of f (x) for the domain –4 ≤ x ≤ 2.
Hence, state the range of values of f (x) based on the given domain.

Solution:
(a)
Given f (x) = |x + 2|
Image of –4 is f(–4) = | –4 + 2| = | –2| = 2
Image of –3 is f(–3) = | –3 + 2| = | –1| = 1
Image of 0 is f(0) = | 0 + 2| = | 2 | = 2
Image of 2 is f(2) = | 2 + 2| = | 4 | = 4

(b)
From (a),
f(–4) = 2
f(–3) = 1
f(0) = 2
f(2) = 4

Determine the point where the graph touches the x-axis.
At x-axis, f (x) = 0
|x + 2| = 0
x + 2 = 0
x = –2

Therefore, range of values of f (x) is 0 ≤ f (x) ≤ 4.

Notation of Function

Posted on April 18, 2020 by user

As shown in figure above, for a function

$f : X \to Y$ , each element x in the domain X has a unique image y in the codomain Y.

The function can be written as:

$\begin{array}{l} y = f (x) \\ o r \\ f : x \mapsto f (x) \end{array}$

For $y = f (x)$ , we say y is a function of x.
f(x) is also called the value of the function f at x.
f(x) is read as "f of x".

Example:
Given the function

$f : x \mapsto 5 x + 1$ , find the value of
a.

$f (2)$
b.

$f (- 3)$
c.

$f (\frac{2}{5})$

Answer:
(a)

$\begin{array}{l} f (x) = 5 x + 1 \\ f (2) = 5 (2) + 1 = 11 \end{array}$

(b)

$\begin{array}{l} f (x) = 5 x + 1 \\ f (- 3) = 5 (- 3) + 1 = - 14 \end{array}$

(c)

$\begin{array}{l} f (x) = 5 x + 1 \\ f (\frac{2}{5}) = 5 (\frac{2}{5}) + 1 = 3 \end{array}$