Home › 2020 › April › Page 60

Monthly Archives: April 2020

3.4.2 Hydraulic System

Posted on by

  1. A hydraulic system applies Pascal's principle in its working mechanism. It can be used as a force multiplier.
  2. In this hydraulic system, a small force, Fl is applied to the small piston X results in a large force, F2 at the large piston Y. The pressure, due to the force, F1, is transmitted by the liquid to the large piston.
  3. According to Pascal’s principle,


Change of Oil Level in a Hydraulic System


In the diagram to the left, when piston-X is pressed down, piston-Y will be push up. The change of the piston levels of the 2 pistons is given by the following equation:

Example 1:
In a hydraulic system the large piston has a cross-sectional area A2 = 200 cm² and the small piston has cross-sectional area A1 = 5 cm². If a force of 250 N is applied to the small piston, what is
a. the pressure exerted on the small piston
b. the force F, produced on the large piston?

Answer:

a. Pressure exerted on the small piston

b. Pressure exerted on the large piston = Pressure exerted on the small piston



Example 2:

A hydraulic lift is to be used to lift a truck masses 5000 kg. If the diameter of the small piston and large piston of the lift is 5cm and 1 m respectively,

a. what gauge pressure in Pa must be applied to the oil?
b. What is the magnitude of the force required on the small piston to lift the truck?

Answer:
a. Weight of the truck,
W = mg
W = (5000)(10) = 50,000N

Area of the big piston


Pressure of the oil


b.
Area of the small piston


According to the Pascal's Principle,


Example 3:

Figure above shows a hydraulic system. The area of surface X is 5 cm² and the area of surface Y is 100 cm². Piston X has been pushed down 10cm. what is the change of liquid level, h, at Piston Y?

Answer:

Distance move by the piston-X, h1 = 10cm
Distance move by the piston-Y, h2 = h
Area of piston-X, A1 = 5 cm²
Area of Piston-Y, A2 = 100 cm²


 

3.4.1 Pascal’s Principle

Posted on by
  1. Pascal's principle states that in a confined fluid, an externally applied pressure is transmitted uniformly in all directions.
  2. Pascal's principle is also known as the principle of transmission of pressure in a liquid.

Q & A

Q: Suggest an experiment to prove Pascal’s Principle.

A:
  1. When the plunger is pushed in, the water squirts equally from all the holes.
  2. This shows that the pressure applied to the plunger has been transmitted uniformly throughout the water.

 

3.3.5 Applications of Atmospheric Pressure

Posted on by

Syringe

  1. When the piston is pulled up, the atmospheric pressure inside the cylinder will decrease.
  2. The atmospheric pressure outside pushes the liquid up into the syringe.

Lift Pump

Siphon

Working Mechanism of Siphon

Sucker Hook


When the sucker is pressed into place, the air inside is forced out. As a result, the pressure inside the sucker become very low. The sucker is then held in position by the high atmospheric
pressure on the outside surface.

Straw


When a person sucks through the straw, the pressure in the straw become low. The atmospheric pressure outside which is higher will force the water into the straw and consequently into the mouth.

Rubber Sucker

Vacuum Cleaner


 

 

 

3.3.4 Measuring Atmospheric Pressure

Posted on by
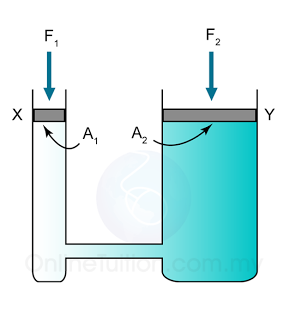
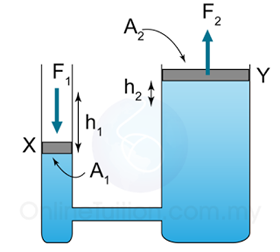
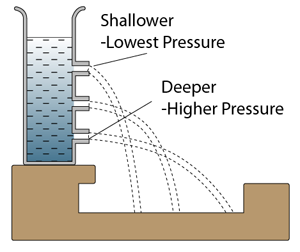
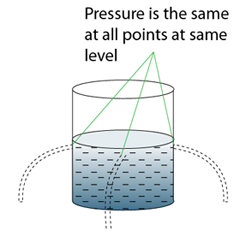
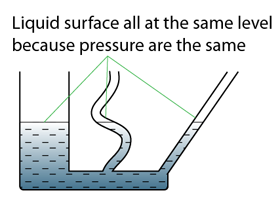
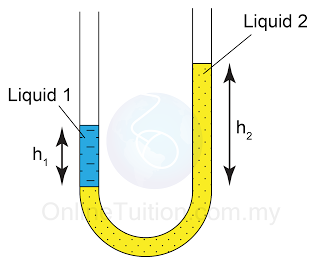
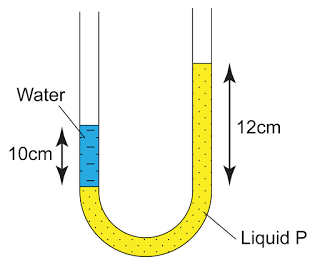
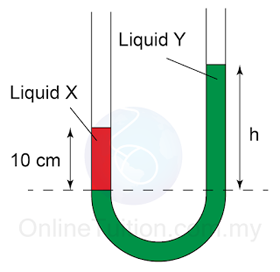
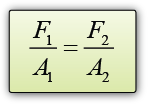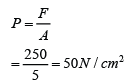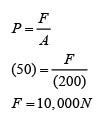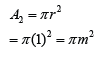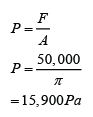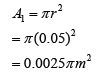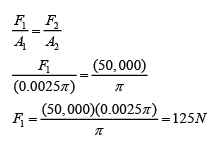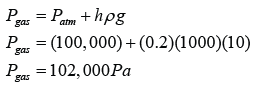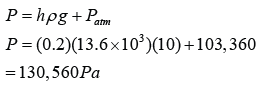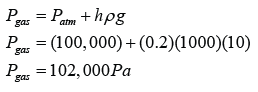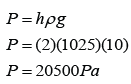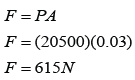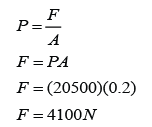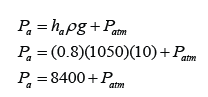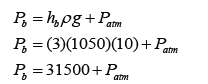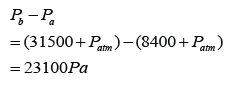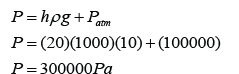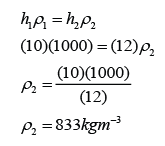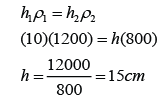  1. Atmospheric pressure can be measured by either
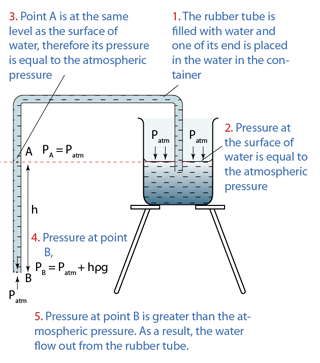
    1. a simple barometer,
    2. a Fortin barometer
    3. an Aneroid barometer.
  2. In SPM, most of the questions asked are related to the simple barometer.
  3. For Fortin barometer and Aneroid barometer, you only need to know their working principle.

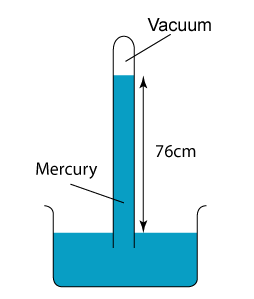
Simple Mercury Barometer

Fortin Barometer.
This image is created by Edal Anton Lefterov and shared under the Creative Commons Attribution-Share Alike 3.0 Unported license.



Aneroid Barometer

Simple Barometer

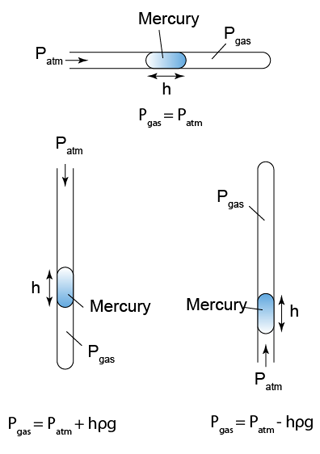
  1. Atmospheric pressure can be measured by a simple barometer.
  2. A thick glass tube (at least 1m long) is filled with mercury completely.
  3. The open end of the tube is covered with a finger and inverted in a trough of mercury.
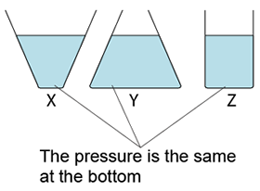
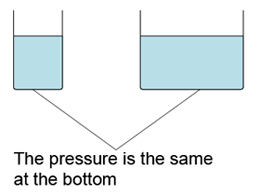
  4. The height of the mercury is proportional to the atmospheric pressure.

Using Simple Mercury Barometer


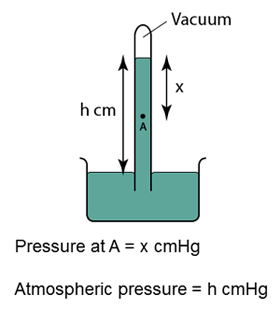
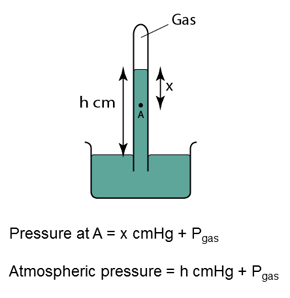
Characteristics of the Mercury Barometer



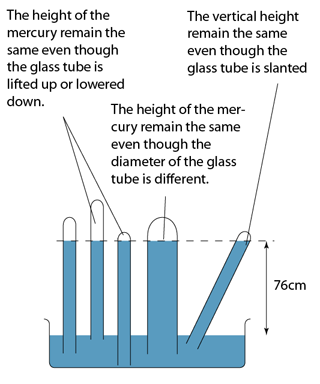
Q and A
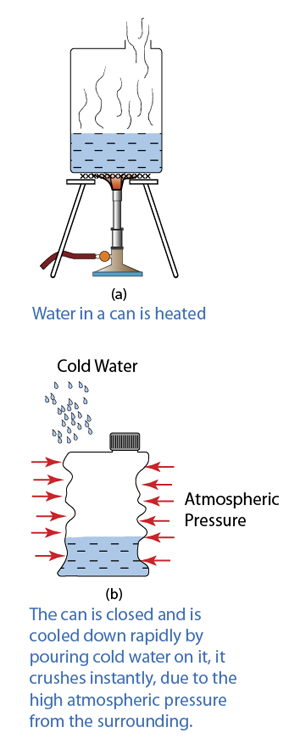
Q: Barometer is usually made up of mercury. Explain why is it not practical to have a water barometer?

A: 
  1. The atmospheric pressure is about 10 meter water, which means it can push the water up to 10 meter height. 
  2. Therefore a water barometer must be at least 10 meter long. 
  3. This is not practical because the glass tube of the barometer may be broken or topple easily. It is also difficult to keep or move such a long tube.

Fortin Barometer

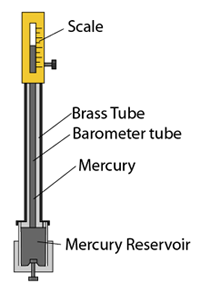
  1. The Fortin barometer is an improved version of the simple mercury barometer.
  2. The barometer tube is encased in a brass frame. This enables it to be carried around easily.
  3. Vernier scale is used for taking reading for extra accuracy.

Q & A

Q: What is the advantages of a Fortin Barometer over a Simple mercury barometer?

A:
  1. Easy to be carried around.
  2. More accurate.

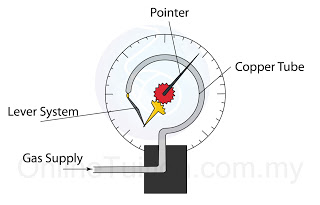
Anaroid Barometer


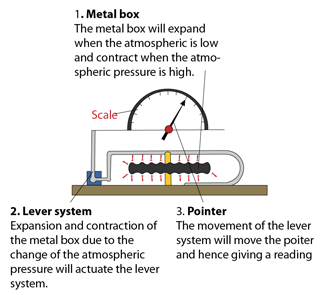
The anaroid barometer is usually used to measure altitude, which is named as altimeter.

Q & A

Q: Explain why the barometer can be used to measure altitude.

A:
The atmospheric pressure is inversely proportional to the altitude. The altitude can be determined from the atmospheric pressure.


Q & A

Q: Why a simple barometer is not suitable to be used to measure altitude?

A:
  1. Hard to be carried
  2. Mercury is volatile. It can evaporate easily
  3. Mercury is poisonous

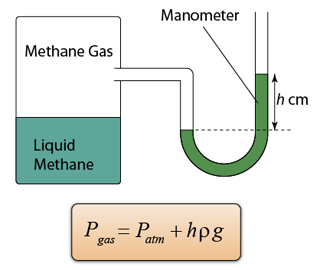
Converting the Unit from cmHg to Pa

Pressure in unit cmHg can be converted to Pa by using the formula

P = hρg

Example 1:

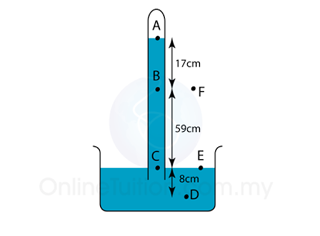
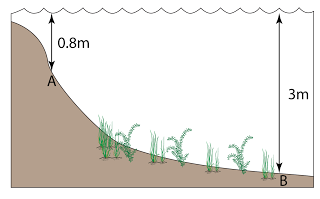
Find the pressure at point A, B, C, D, D, E and F in the unit of cmHg and Pa. [Density of mercury = 13600 kg/m³]

Answer:
Pressure in unit cmHg  Pressure in unit Pa 
PA = 0

PB = 17 cmHg

PC = 17 + 59 = 76 cmHg

PD = 76 + 8 = 84 cmHg

PE = 76 cmHg

PF = 76 cmHg		 PA = 0

PB = hρg = (0.17)(13600)(10) = 23,120 Pa

PC = hρg = (0.76)(13600)(10) = 103,360 Pa

PD = hρg = (0.84)(13600)(10) = 114,240 Pa

PE = hρg = (0.76)(13600)(10) = 103,360 Pa

PF = hρg = (0.76)(13600)(10) = 103,360 Pa


Example 2:

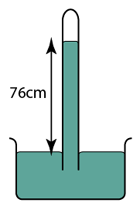
Figure above shows a simple mercury barometer. What is the value of the atmospheric pressure shown by the barometer? [Density of mercury = 13600 kg/m³]

Answer:
Atmospheric Pressure,

P = 76 cmHg

or

P = hρg = (0.76)(13600)(10) = 103360 Pa


Example 3:

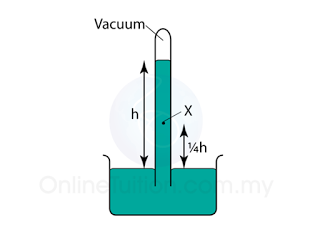
In above, the height of a mercury barometer is h when the atmospheric pressure is 101 000 Pa.
What is the pressure at X?

Answer:
Atmospheric Pressure,
Patm = h cmHg = 101 000 Pa

Pressure at X,
PX = (h - ¼h) = ¾h cmHg

PX = ¾ x 101 000 = 75 750 Pa


Example 4:

Figure above shows a mercury barometer whereby the atmospheric pressure is 760 mm Hg on a particular day. Determine the pressure at point
a. A,
b. B,
c. C.
[Density of Mercury = 13 600 kg/m³]
Answer:
a.
PA = 0

b.
PB = 50 cmHg

or

PB = hρg = (0.50)(13600)(10) = 68 000 Pa

c.
PC = 76 cmHg

or

PC = hρg = (0.76)(13600)(10) = 103 360 Pa


Example 5:

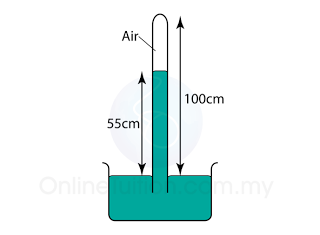
Figure above shows a simple barometer, with some air trapped in the tube. Given that the atmospheric pressure is equal to 101000 Pa, find the pressure of the trapped gas. [Density of Mercury = 13 600 kg/m³]

Answer:
Pressure of the air = Pair
Atmospheric pressure = Patm

Pair + 55 cmHg = Patm

Pair
= Patm - 55 cmHg
= 101 000 - (0.55)(13 600)(10)
= 101 000 - 74 800
= 26 200 Pa


Example 6:
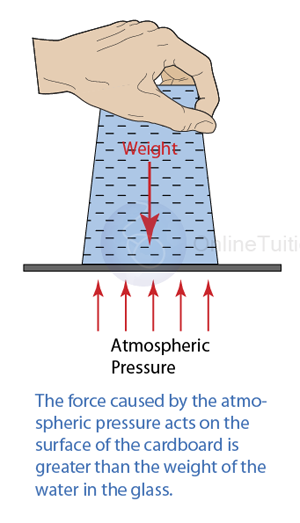
If the atmospheric pressure in a housing area is 100 000 Pa, what is the magnitude of the force exerted by the atmospheric gas on a flat horizontal roof of dimensions 5m × 4m?

Answer:
Area of the roof = 5 x 4 = 20 m²

Force acted on the roof

F = PA
F = (100 000)(20)
F = 2,000,000 N


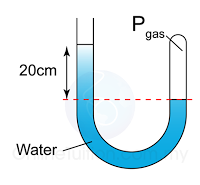
Example 7:


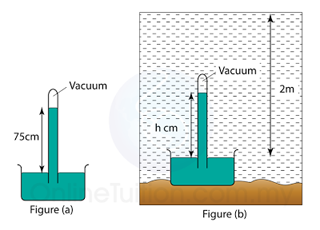
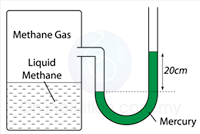
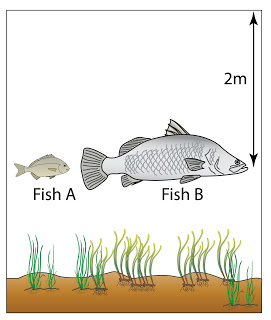
Figure(a) above shows the vertical height of mercury in a mercury barometer in a laboratory. Figure(b) shows the mercury barometer in water at a depth of 2.0 m.

Find  the vertical height (h) of the mercury in the barometer in the water. Given that the pressure at a depth of 10 m from the water surface is 75 cmHg. [Density of water = 1000 kg/m³, Density of mercury = 13 600 kg/m³]

Answer:
Atmospheric pressure,
Patm = 75 cmHg

Pressure caused by the water,
Pwater = 2/10 x 75 = 15cmHg

Pressure in 2m under water
= 75 + 15 = 90 cmHg

Vertical height of the mercury = 90cm

 

3.3.3 Measuring Gas Pressure

Posted on by

Instruments Used to Measure Gas Pressure

  1. The pressure of the gas in a container can be measured by using
    1. Bourdon gauge
    2. Manometer
  2. In SPM, almost all calculation question about using instruments to find gas pressure in a container are related to manometer. Therefore it's important for you to know the concept behind this instrument.
  3. For the Bourdon Gauge, you need to know its working mechanism.

Bourdon Gauge


  1. A Bourdon gauge is used to measure to gas pressure in a container.
  2. There are 3 important components in a Bourdon gauge
  3. the copper tube
  4. the lever system
  5. the pointer

Working Mechanism of a Bourdon Gauge

  1. When the gauge is connected to a gas supply, the gas pressure will straighten the copper tube.
  2. The copper tube exerts a force on the lever system and hence move the pointer. The movement of the copper tube is magnified by the lever system
  3. The pointer rotates and give a reading (in unit of Pascal).

Manometer


  1. A manometer is a U-shape tube filled with some liquid (usually mercury).
  2. Manometer is a device used to measure gas pressure in a container.
  3. The pressure of the gas is equal to the sum of the atmospheric pressure and pressure due to the column of liquid.
Pgas = Patm + Pliquid

Note:

There are a few points we need to know when using a manometer
  1. Difference in gas pressure at difference level can be ignored.
  2. Pressure on the surface of liquid is equal to the gas pressure in contact.
  3. Pressure that cause by liquid = hρg.
  4. For a given liquid, the pressures at any point of the same level are the same.
  5. For different liquid with different density, pressure at two different level will be different.

Example 1:

Figure above shows a manometer containing mercury connected to a tank with methane liquid and gas. Find the pressure of the gas supply in the units cmHg and Pa.
[Density of mercury = 13.6 x 10³ kg/m³; atmospheric pressure = 76 cmHg]

Answer:
Pressure of the gas in cmHg

P = 20 + 76 = 96 cmHg

Pressure of gas in Pa
The atmospheric pressure,

Pressure of the gas,



Example 2:

Figure above shows the mercury levels in a manometer used to measure the pressure of a gas supply. How much is the gas pressure greater than the atmospheric?

Answer:

Pgas = Pmercury + Patm

Pgas - Patm = Pmercury = 5 cmHg

  1. The pressure of the gas trapped in a capillary tube depends on the position of the tube.
  2. Figure below shows the pressure of the gas when the capillary tube is horizontal, vertical and vertically upside down.

Example 3:

Figure above shows 3 identical capillary tubes with one end sealed and containing a column of mercury. PA, PB and PC are the gas pressure in the capillary tubes respectively. Find the value of PA, PB and PC. [Atmospheric pressure = 76cmHg]

Answer:

PA = 76cmHg

PB = 76cmHg + 2cmHg = 78cmHg

PC = 76cmHg - 2cmHg = 74cmHg


Example 4:


Figure above shows some air trapped in a J-tube. Find the pressure of the trapped air. [Density of water = 1000 kg/m³; Atmospheric pressure = 100,000 Pa]
Answer:


 

3.3.2 Atmospheric Pressure

Posted on by
  1. On the surface of the earth, there is a thick layer of gas called the atmosphere. The atmosphere consists of various types of gas called the atmospheric gas.
  2. The atmospheric gases collide on the surface of the earth and hence exert a pressure on the surface of the earth, called the atmospheric pressure.
  3. The atmospheric pressure can be measured in the unit of atm, mmHg or Pa. The atmospheric pressure at sea level is taken to be 1 atm, which is approximately 760 mmHg or 101,000 Pa.

Characteristics of Atmospherics Pressure

  1. Decreases with altitude
    The atmospheric pressure changes accordingly to the altitude. Altitude is the height above sea level. The greater the altitude, the lower the atmospheric pressure.
  2. Act equally in all direction
    The atmospheric pressure acts on every object in the atmosphere. It acts equally in all direction.
  3. Atmospheric pressure is ~ 100,000Pa at sea level
    On the surface of the earth, the atmospheric pressure can be as high as 101,000 Pa.

Unit Used to Measure Atmospheric Pressure

  1. The following are the unit used to measure atmospheric pressure
    1. Pascal (Pa)
      1 Pa = 1 N/m²
    2. Standard Atmospheric Pressure (atm)
      1 atm = Atmospheric Pressure at sea level ( = 101,325 Pa)
    3. mmHg (also known as torr)
      1 mmHg = 1/760 atm (roughly equal to the liquid pressure exerted by a millimetre of mercury).
    4. milibar (Not used in SPM)
  2. In SPM, usually we use the unit cmHg, instead of mmHg.

Proof of Existence of Atmospheric Pressure

The existence of the atmospheric pressure can be proved by the following experiments.
  1. Crushing can experiment
  2. Water cover with cardboard does not flow out
  3. Magdeburg Hemisphere

Crushing Can Experiment

  1. When a can filled with hot water is closed and is cooled down rapidly by pouring cold water on it, it will crush instantly.
  2. This experiment proves that there is a huge atmospheric pressure exerts on everything on the surface of the earth.

Water cover with cardboard does not flow out

  1. The cardboard does not fall and the water remains in the glass even though it's not supported by anything.
  2. This is because the force caused by the atmospheric pressure acts on the surface of the cardboard is greater than the weight of the water in the glass. This experiment proves that atmospheric pressure is present on the surface of the earth.

Magdeburg Hemisphere

  1. When the air inside the hemisphere is pumped out so that it becomes a vacuum, the hemisphere cannot be separated even by a very great force.
  2. This is because when the air is pumped out, the pressure inside the hemisphere becomes very low.
  3. The atmospheric pressure exerts a strong force on the outer surface of the hemisphere, holding the hemisphere tightly together.

 

3.3.1 Gas Pressure

Posted on by
  1. Gas pressure is the force per unit area exerted by the gas molecules as they collide with the surface of an object.
  2. In SPM, especially in paper 2 essay question, you need to know how the gas pressure is produced. (See question below)
Question:
Explain how gas pressure is produced in a closed container?

Answer:
  1. Gas molecules in a container are in constant and random motion.
  2. As a result, the gas molecules collide on the wall of the container.
  3. After colliding on the wall, the gas molecules bounce off, and the direction change creating a change of momentum to the molecule of the gas.
  4. The change of momentum produces a force on the wall.
  5. The force per unit area is the pressure on the wall.

 

 

3.2.3 Applications of Liquid Pressure

Posted on by

Dam


  1. The wall of the dam is built thicker at the bottom to withstand a higher pressure.
  2. The generator is placed at the lower part so that the pressure of the water is high enough to drive the turbine.

Submarine


In deep sea, the pressure of the water is tremendously high. Hence the body of the submarine is thick and built by strong material

Measuring Blood Pressure


When measuring blood pressure, the inflatable cuff of the sphygmomanometer should be at the same level with the heart so that the pressure measured is equal to the blood pressure of the heart.

Intravenous Transfusion


For intravenous transfusion (IV), the bottle is hung at an elevated position to ensure that the liquid in the IV bottle gains sufficient pressure to flow into the vein of the patient.

Water Tower


The water tower is built at high place so that the water has sufficient pressure to flow to consumer’s house.

 

3.2.2 Nature of Liquid Pressure

Posted on by

The pressure caused by a liquid has the following characteristics:

  1. Pressure in liquid does not depends on
    1. the shape of the container.

      Eventhough the shape of the containers are different, the pressure at the bottom are still the same if the depth of water are the same.
    2. the size of the container.

      Eventhough the size of the two container are different, the pressure at the bottom are still the same if the depth of water are the same.
    3. the area of its surface.

      Eventhough the area of A and B are different, the pressure at the two areas are still the same if the depth of water are the same.

Pressure Increases with Depth

  1. The deeper the liquid, the faster the liquid spurts out.
  2. In conclusion, the pressure in a liquid increases with depth.

Pressure Depends on the Vertical Depth, But not the Length of Liquid Column.


Pressure at A = Pressure at B

All Points at the Same Level in a Liquid are at the Same Pressure


The level of the surface of a liquid in a container is always the same because for a given liquid, the pressure is always equal at the same level.

Pressure Does Not Depend on the Surface Area of the Object.


Pressure exerted on the small fish
= Pressure exerted on the big fish

Pressure Acts in All Direction


The pressure at any point of a liquid acts equally in all direction.

 

 

3.2.1 Liquid Pressure

Posted on by
  1. Pressure in liquid is owing to the weight of the liquid acting on the surface of any objects in the liquid.
  2. Pressure of a liquid is directly proportional to
    1. the gravitational field strength
    2. the depth
    3. density of the liquid.
  3. Pressure in liquids is not affected by the size or shape of the object.
  4. The pressure caused by a liquid and the pressure in a liquid can be determined by using the equation below:

Pressure Caused by Liquid




Pressure in Liquid


Example 1:


The diagram shows 2 fishes in water. The density of the water is 1025 kg/m³. The surface area of fish A is 300 cm² and the surface area of fish B is 2000cm². Find
a. the pressure exerted by the water on fish A.
b. the pressure exerted by the water on fish B.
c. the force exerted by the water on fish A.
d. the force exerted by the water on fish B.

Answer:
This question would like us to compare the liquid pressure exerted on 2 objects of different size in the same depth of water.

a.
Depth, h = 2m
Density, ρ = 1025 kg/m³
Gravitational Field Strength, g = 10 N/kg

Pressure exerted by water on fish A,


b. Pressure exerted by water on fish B,


(Note: Pressure exerted both fishes are the same. Pressure caused by liquid is not affected by the size or shape of the objects)

c. Surface area of fish A, A1 = 300 cm² = 0.03 m²

Force exerted by the liquid pressure,


d. Surface area of fish B, A2 = 2000cm² = 0.2 m²

Force exerted by the liquid pressure,



Example 2:


Figure above shows the cross section of a sea near a seaside. Find the difference of the pressure between point A and point B. [Density of seawater = 1050kg/m³]

Answer:
Density, ρ = 1050kg/m³
Gravitational Field Strength, g = 10 N/kg

At point A:
Depth, h = 0.8 m


At point B:
Depth, h = 3 m


Pressure Difference



Example 3:
Find the pressure at a depth of 20 m in water when the atmospheric pressure is 100000 Pa. The density of water is 1000 kg/m³.

Answer:
(Caution: Pressure in liquid = Pressure caused by liquid + Atmospheric Pressure)

Depth, h = 20m
Density,  = 1000 kg/m³
Gravitational Field Strength, g = 10 N/kg
Atmospheric Pressure, Patm = 100000 Pa

Pressure in water,



  1. Usually, a U-tube is used to compare and measure density of liquids.
  2. The density of the 2 liquids is related by the equation:

Example 4:


Figure above shows a U-tube filled with water and liquid P. Liquid P is insoluble in water. Given that the density of water is 1000kg/m³, find the density of liquid P.

Answer:
h1 = 10cm
h2 = 12 cm
ρ1 = 1000kg/m³
ρ2 = ?



The density of liquid P = 833 kg/m³


Example 5:

The diagram shows a U-tube filled with two types of liquid, X and Y which are not mixable. If the density of liquid X and liquid Y are 1200 kg/m³ and 800 kg/m³ respectively, find the value of h.

Answer:
h1 = 10cm
h2 = h
ρ1 = 800kg/m³
ρ2 = 1200kg/m³