4.7.6 Penaakulan Matematik, SPM Praktis (Kertas 2)

Soalan 12 (5 markah):
(a) Nyatakan sama ada pernyataan majmuk berikut adalah benar atau palsu.
2 > 3 dan (–2)³ = –8

(b) Tulis dua implikasi berdasarkan pernyataan berikut:
a > b jika dan hanya jika a – b > 0

(c) Jadual 1 menunjukkan bilangan sisi dan bilangan paksi simetri bagi beberapa poligon sekata.

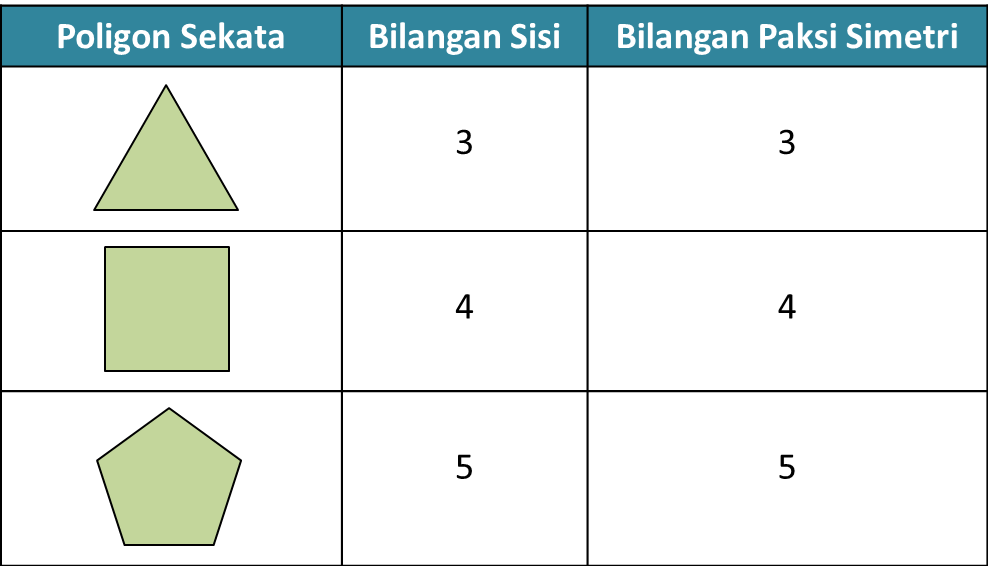Jadual 1

Buat satu kesimpulan secara aruhan dengan melengkapkan pernyataan berikut:
Bilangan paksi simetri bagi sebuah poligon sekata dengan n sisi ialah __________.

Penyelesaian:
(a)
Palsu. Nilai bagi 2 adalah kurang daripada 3, 2 < 3.

(b)
Implikasi 1: Jika a > b, maka a – b > 0
Implikasi 2: Jika a – b > 0, maka a – b > 0

(c)
Bilangan paksi simetri bagi sebuah poligon sekata dengan n sisi ialah
Bilangan sisi poligon sekata = bilangan  paksi simetri poligon sekata

Soalan 13 (5 markah):
(a) Nyatakan sama ada pernyataan-pernyataan berikut ialah pernyataan benar atau pernyataan palsu.
$\begin{array}{l}\left(\text{i}\right)\text{ { }}\subset \{S,E,T\}\\ \left(\text{ii}\right)\text{ { 1 }}\subset \{1,2,3\}=\{1,2,3\}\end{array}$

(b) Rajah 7 menunjukkan tiga corak pertama daripada suatu jujukan corak-corak.

Rajah 7

Diberi bahawa diameter setiap bulatan ialah 20 cm.
(i) Buat satu kesimpulan umum secara aruhan bagi luas kawasan tidak berlorek.

(ii) Seterusnya, hitung luas kawasan tidak berlorek untuk corak ke-5.

Penyelesaian:
(a)(i) Benar

(a)(ii) Palsu

(b)(i)
Luas kawasan tidak berlorek (pertama)
= (20 × 20) – π(10)²
= 400 – 100π
= 100 (4 – π)

Luas kawasan tidak berlorek (kedua)
= 4 × 100 (4 – π)
= 400 (4 – π)

Luas kawasan tidak berlorek (ketiga)
= 9 × 100 (4 – π)
= 900 (4 – π)
100 (4 – π), 400 (4 – π), 900 (4 – π), …
10² (4 – π), 20² (4 – π), 30² (4 – π), …

Kesimpulan umum = n² (4 – π)
n = 10, 20, 30, …


(b)(ii)
Luas kawasan tidak berlorek untuk corak ke-5
= 50² (4 – π)
= 2500 (4 – π)