Soalan 7:
Cari julat nilai k jika persamaan kuadratik 3(x2 – kx – 1) = k – k2 mempunyai dua punca nyata yang berbeza.
Penyelesaian:
3(x2−kx−1)=k−k23x2−3kx−3−k+k2=03x2−3kx+k2−k−3=0a=3,b=−3k,c=k2−k−3Dua punca nyata berbeza.b2−4ac>0(−3k)2−4(3)(k2−k−3)>09k2−12k2+12k+36>0−3k2+12k+36>0−k2+4k+12>0k2−4k−12<0(k+2)(k−6)<0k=−2,6

Julat nilai k ialah −2<k<6.
Cari julat nilai k jika persamaan kuadratik 3(x2 – kx – 1) = k – k2 mempunyai dua punca nyata yang berbeza.
Penyelesaian:
3(x2−kx−1)=k−k23x2−3kx−3−k+k2=03x2−3kx+k2−k−3=0a=3,b=−3k,c=k2−k−3Dua punca nyata berbeza.b2−4ac>0(−3k)2−4(3)(k2−k−3)>09k2−12k2+12k+36>0−3k2+12k+36>0−k2+4k+12>0k2−4k−12<0(k+2)(k−6)<0k=−2,6

Julat nilai k ialah −2<k<6.
Soalan 8 (4 markah):
Fungsi kuadratik f ditakrifkan oleh f(x) = x2 + 4x + h, dengan keadaan h ialah pemalar.
(a) Ungkapkan f(x) dalam bentuk (x + m)2 + n, dengan keadaan m dan n ialah pemalar.
(b) Diberi nilai minimum bagi f(x) ialah 8, cari nilai h.
Penyelesaian:
(a)
f(x) = x2 + 4x + h
= x2 + 4x + (2)2 – (2)2 + h
= (x + 2)2 – 4 + h
(b)
Diberi nilai minimum bagi f(x) = 8
– 4 + h = 8
h = 12
Fungsi kuadratik f ditakrifkan oleh f(x) = x2 + 4x + h, dengan keadaan h ialah pemalar.
(a) Ungkapkan f(x) dalam bentuk (x + m)2 + n, dengan keadaan m dan n ialah pemalar.
(b) Diberi nilai minimum bagi f(x) ialah 8, cari nilai h.
Penyelesaian:
(a)
f(x) = x2 + 4x + h
= x2 + 4x + (2)2 – (2)2 + h
= (x + 2)2 – 4 + h
(b)
Diberi nilai minimum bagi f(x) = 8
– 4 + h = 8
h = 12
Soalan 9 (3 markah):
Cari julat nilai x dengan keadaan fungsi kuadratik f(x) = 6 + 5x – x2 ialah negatif.
Penyelesaian:
(a)
f(x) < 0
6 + 5x – x2 < 0
(6 – x)(x + 1) < 0
x < –1, x > 6
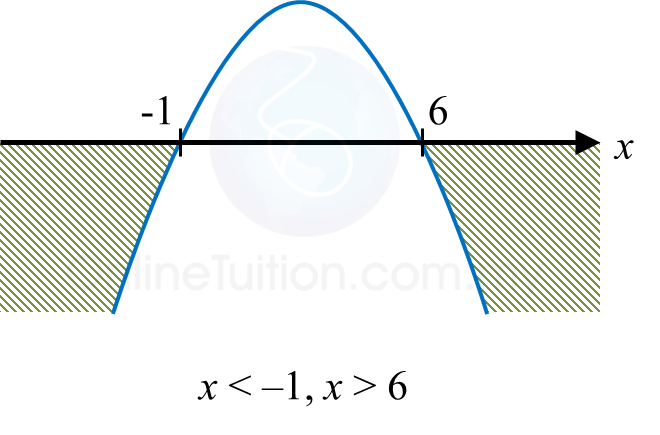
Cari julat nilai x dengan keadaan fungsi kuadratik f(x) = 6 + 5x – x2 ialah negatif.
Penyelesaian:
(a)
f(x) < 0
6 + 5x – x2 < 0
(6 – x)(x + 1) < 0
x < –1, x > 6
